d) 3
e) 4
Exercícios Funções
Exponenciais e Logarítmicas
4. (Ufpr 2014) Uma pizza a 185°C foi retirada de um
forno quente. Entretanto, somente quando a
temperatura atingir 65°C será possível segurar um de
seus pedaços com as mãos nuas, sem se queimar.
Suponha que a temperatura T da pizza, em graus
Celsius, possa ser descrita em função do tempo t, em
2x −5
1. (Udesc 2014) Considere a função f(x) = 2
.
Sejam (a1, a2 , a3 ,...) uma progressão aritmética de
razão 3 e f(a1 ) =
1
. Analise as proposições.
8
I. a53 = 157
II. A soma dos 11 primeiros termos da progressão
aritmética é 145.
III. f(a5 ) = 221
IV. (f(a1 ),f(a2 ),f(a3 ),...) é uma progressão geométrica
de razão 64.
Assinale a alternativa correta.
a) Somente as afirmativas I e III são verdadeiras.
b) Somente as afirmativas I, III e IV são verdadeiras.
c) Somente as afirmativas I e II são verdadeiras.
d) Somente as afirmativas III e IV são verdadeiras.
e) Todas as afirmativas são verdadeiras.
5. (Unicamp 2014) A altura (em metros) de um
arbusto em uma dada fase de seu desenvolvimento
pode ser expressa pela função h(t) = 0,5 + log3 (t + 1),
onde o tempo t ≥ 0 é dado em anos.
2. (Ufsc 2014) Assinale a(s) proposição(ões)
CORRETA(S).
01) O domínio da função f dada por f(x) =
minutos, pela expressão T = 160 × 2−0,8×t + 25. Qual o
tempo necessário para que se possa segurar um
pedaço dessa pizza com as mãos nuas, sem se
queimar?
a) 0,25 minutos.
b) 0,68 minutos.
c) 2,5 minutos.
d) 6,63 minutos.
e) 10,0 minutos.
x −1
é
x+3
{x ∈ ; x ≥ 1}.
02) O único valor inteiro que pertence à solução da
a) Qual é o tempo necessário para que a altura
aumente de 0,5 m para 1,5 m?
b) Suponha que outro arbusto, nessa mesma fase de
desenvolvimento, tem sua altura expressa pela
função composta g(t) = h(3t + 2). Verifique que a
diferença g(t) − h(t) é uma constante, isto é, não
depende de t.
inequação x2 − 4x + 3 < 0 é 2.
04) O conjunto solução da equação modular
| 3 − 2x |=| x − 2 | é S = {1}.
− x, se x < 0
08) A função R(x) = x 2 , se 0 ≤ x ≤ 1 é crescente em
1, se x > 1
todo o seu domínio.
16) Se uma função f : →
é simultaneamente par
e ímpar, então f(1) = 0.
32) Os gráficos das funções f : → e g : → ,
6. (Pucrs 2014) O modelo da cobertura que está
sendo colocada no Estádio Beira-Rio está
representado na figura abaixo.
dadas respectivamente por f(x) = x 2 e g(x) = 2 x ,
para todo x real, se intersectam em exatamente
um único ponto.
64)
x 2 = x para todo x real.
3. (Mackenzie 2014) Seja f :
+
→
+
uma função
tal que f ( x + y ) = f ( x ) ⋅ f ( y ) para quaisquer x ∈
y∈
+.
4
Se f (1) = 8, o valor de f é
3
a) 16
1
b)
3
1
c)
4
www.soexatas.com
+
e
Colocada devidamente em um plano cartesiano, é
possível afirmar que, na forma em que está, a linha
em destaque pode ser considerada uma restrição da
representação da função dada por
a) y = log(x)
b) y = x 2
c) y = x
d) y = − x
e) y = 10 x
Página 1
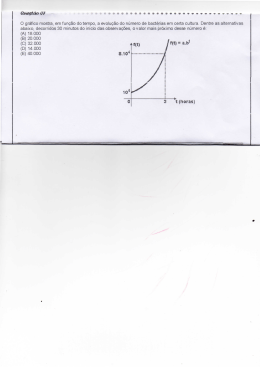
7. (Ufrn 2013) A pedido do seu orientador, um bolsista
de um laboratório de biologia construiu o gráfico a
seguir a partir dos dados obtidos no monitoramento do
crescimento de uma cultura de micro-organismos.
2 ≅ 1,4, podemos concluir que a
população dessa cidade atingiu a marca
dos 3600 habitantes em meados do ano:
a) 2005
b) 2002
c) 2011
d) 2007
e) 2004
10. (Uem 2012) Considere a seguinte função
2
Analisando o gráfico, o bolsista informou ao orientador
que a cultura crescia segundo o modelo matemático,
N = k ⋅ 2at , com t em horas e N em milhares de microorganismos.
Para constatar que o modelo matemático apresentado
pelo bolsista estava correto, o orientador coletou
novos dados com t = 4 horas e t = 8 horas.
Para que o modelo construído pelo bolsista esteja
correto, nesse período, o orientador deve ter obtido
um aumento na quantidade de micro-organismos de
a) 80.000.
b) 160.000.
c) 40.000.
d) 120.000.
8. (Pucrs 2013) A desintegração de uma substância
radioativa é um fenômeno químico modelado pela
fórmula q = 10 ⋅ 2k⋅t , onde q representa a quantidade
de substância radioativa (em gramas) existente no
instante t (em horas). Quando o tempo t é igual a 3,3
horas, a quantidade existente q vale 5. Então, o valor
da constante k é
a) − 35 5
b) − 33 10
c) − 5 33
d) − 10 33
e) − 100 33
9. (Espm 2013) Em 1997 iniciou-se a ocupação de
uma fazenda improdutiva no interior do país, dando
origem a uma pequena cidade. Estima-se que a
população dessa cidade tenha crescido segundo a
função P = 0,1 + log 2 ( x − 1996 ) , onde P é a população
no ano x, em milhares de habitantes. Considerando
www.soexatas.com
f(x) = 42x − x −1 cujo domínio é conjunto dos números
reais. Com relação a essa função, assinale o que for
correto.
01) O mínimo da função f ocorre em x = 0.
02) O conjunto solução da inequação f (x) <1 é
1
S = x ∈ | − < x < 1 .
2
04) Para x = 0, tem-se log2 f(x) = −2 .
08) O conjunto solução da inequação f (x) > 8 é
1 − 21
1 + 21
S = x ∈ | x <
ou x >
.
4
4
16) log3 f (1) não existe.
11. (Unioeste 2012) O Saccharomyces cerevisiae é
um fungo com bastante importância econômica. É
utilizado como fermento para a massa de pão,
produzindo dióxido de carbono e fazendo a massa
crescer. É também utilizado na produção de bebidas
alcoólicas fermentadas, pois converte o açúcar em
álcool etílico. Sob certas condições de cultura, este
fungo cresce exponencialmente de forma que a
quantidade presente em um instante t dobra a cada
1,5 horas. Nestas condições, se colocarmos uma
quantidade q0 deste fungo em um meio de cultura, a
quantidade q(t) existente do fungo, decorridas t horas
com t ∈ [0, ∞ ), pode ser calculada pela função
a) q ( t ) = q0 43t .
b) q ( t ) =
4 2
t q0 + q0 .
9
2
3
c) q ( t ) = q0 .
2
2t
3
d) q ( t ) = q0 .
2
3
e) q ( t ) = 4 t q0 .
12. (Ucs 2012) Um modelo matemático para
determinar o número de bactérias em determinado
objeto é a função definida por N ( t ) = 500 ⋅ 2t , em que t
é o tempo, em horas, a partir da observação inicial.
Segundo esse modelo, o tempo, em horas, para que a
quantidade de bactérias no objeto atinja 7.000, é dado
por um número pertencente ao intervalo
a) [99, 100].
b) [13, 14].
c) [6, 7].
Página 2
d) [3, 4].
e) [1, 2].
13. (Ufpr 2012) Um grupo de cientistas decidiu utilizar
o seguinte modelo logístico, bastante conhecido por
matemáticos e biólogos, para estimar o número de
pássaros, P(t), de determinada espécie numa área de
500
proteção ambiental: P(t) =
, sendo t o tempo
1 + 22− t
em anos e t = 0 o momento em que o estudo foi
iniciado.
a) Em quanto tempo a população chegará a 400
indivíduos?
b) À medida que o tempo t aumenta, o número de
pássaros dessa espécie se aproxima de qual valor?
Justifique sua resposta.
14. (Uftm 2012) A população P de um país no ano t
pode ser estimada através da função
P(t) = m ⋅ nt −2011, para n ≠ 0. Sabendo-se que a
população atual desse país é de 15,3 milhões de
habitantes, e que sua taxa anual de crescimento é de
m
2%, então,
é igual a
n
6
a) 1,2 x 10 .
6
b) 1,5 x 10 .
7
c) 1,2 x 10 .
7
d) 1,5 x 10 .
8
e) 1,2 x 10 .
15. (Ufpe 2012) Em uma aula de Biologia, os alunos
devem observar uma cultura de bactérias por um
intervalo de tempo e informar o quociente entre a
população final e a população inicial. Antônio observa
a cultura de bactérias por 10 minutos e informa um
valor Q. Iniciando a observação no mesmo instante
que Antônio, Beatriz deve dar sua informação após 1
hora, mas, sabendo que a população de bactérias
obedece à equação P ( t ) = P0 ⋅ ekt , Beatriz deduz que
encontrará uma potência do valor informado por
Antônio. Qual é o expoente dessa potência?
16. (Ufpr 2012) Uma quantia inicial de R$ 1.000,00 foi
investida em uma aplicação financeira que rende juros
de 6%, compostos anualmente. Qual é,
aproximadamente, o tempo necessário para que essa
quantia dobre? (Use log2 (1,06) ≈ 0,084.)
17. (Espcex (Aman) 2012) Na pesquisa e
desenvolvimento de uma nova linha de defensivos
agrícolas, constatou-se que a ação do produto sobre a
população de insetos em uma lavoura pode ser
descrita pela expressão N ( t ) = N0 ⋅ 2kt , sendo N0 a
população no início do tratamento, N(t), a população
após t dias de tratamento e k uma constante, que
descreve a eficácia do produto. Dados de campo
mostraram que, após dez dias de aplicação, a
www.soexatas.com
população havia sido reduzida à quarta
parte da população inicial. Com estes
dados, podemos afirmar que o valor da
constante de eficácia deste produto é igual a
a) 5−1
b) −5 −1
c) 10
d) 10 −1
e) −10−1
Solução Funções Exponenciais
e Logarítmicas
Resposta da questão 1:
[B]
1
e a1 o primeiro termo da progressão
8
aritmética (a1, a2 , a3 , K) de razão igual a 3, vem
Sendo f(a1 ) =
22a1−5 =
1
⇔ 22a1−5 = 2−3
8
⇔ a1 = 1.
Assim, o termo de ordem n da progressão aritmética
(a1, a2 , a3 , K) é
an = 1 + (n− 1) ⋅ 3 = 3n − 2.
[I] Verdadeira. Tem-se
a53 = 3 ⋅ 53 − 2 = 157.
[II] Falsa. De fato, sendo S11 a soma dos 11
primeiros termos da progressão aritmética
(a1, a2 , a3 , K), vem
1 + 3 ⋅ 11 − 2
S11 =
⋅ 11 = 176.
2
[III] Verdadeira. Como a5 = 3 ⋅ 5 − 2 = 13, temos
f(a5 ) = f(13) = 22⋅13 −5 = 221.
[IV] Verdadeira. Devemos mostrar que
f(an+1 )
= 64
f(an )
para todo n ≥ 1. Com efeito,
f(an+1 ) 22⋅(3⋅(n+1)−2)−5 26n−3
=
=
= 64.
f(an )
22⋅(3n− 2)−5
26n−9
Página 3
Resposta da questão 2:
02 + 16 = 18.
[01] Incorreto. Lembrando que uma função está bem
definida apenas quando se conhece o seu
domínio, o contradomínio e a lei de associação,
vamos supor que a proposição seja:
O maior subconjunto dos números reais para o
qual a função f, dada por f(x) =
x −1
, está
x+3
definida é {x ∈ ; x ≥ 1}.
g apresentam pelo menos um
ponto de interseção no intervalo
1
−1, − 2 (esboce os gráficos para concluir que
existe um único ponto nesse intervalo).
[64] Incorreto. Suponhamos por absurdo que
x 2 = x, para todo x real. Nesse caso, teríamos
x = x2 = ( − x)2 = − x, o que obviamente vale
apenas para x = 0. Na verdade,
x real.
x 2 = | x |, para todo
Desse modo,
Resposta da questão 3:
[A]
x −1
≥ 0 ⇔ x < −3 ou x ≥ 1
x+3
Se f(x + y) = f(x) ⋅ f(y) para quaisquer x ∈
e, portanto, o maior subconjunto dos números
reais para o qual a função f está definida é
{x ∈ ; x < −3 ou x ≥ 1}.
[02] Correto. Tem-se
x2 − 4x + 3 < 0 ⇔ (x − 1) ⋅ (x − 3) < 0
⇔ 1 < x < 3.
Portanto, a única solução inteira da inequação
x 2 − 4x + 3 < 0 é x = 2.
| 3 − 2x | = | x − 2 | ⇒ 3 − 2x = ±(x − 2)
5
.
3
5
Por conseguinte, S = 1, .
3
e
(a > 0). Assim, f(1) = 8
4
4
implica em a = 8 e, portanto, f = 8 3 = 24 = 16.
3
Resposta da questão 4:
[C]
T = 160 ⋅ 2−0,8⋅t + 25
65 = 160 ⋅ 2−0,8⋅t + 25
2−0,8t = 1 4
2−0,8t = 2−2
−0,8 ⋅ t = −2
t = 2,5 minutos
Resposta da questão 5:
a) O valor de t para o qual se tem h(t) = 0,5 é
[08] Incorreto. A função f é decrescente para x < 0.
0,5 = 0,5 + log3 (t + 1) ⇔ t = 0.
[16] Correto. Se f é simultaneamente par e ímpar,
então f( − x) = f(x) e f( −x) = −f(x), para todo x
Para h(t) = 1,5, obtemos
real. Daí, segue-se que f(x) = f( − x) = 0 para todo
x real.
[32] Incorreto. Como f(2) = g(2) = 4, segue-se que o
ponto (2, 4) é comum aos gráficos de f e de g.
Além disso, há pelo menos mais um ponto de
1
interseção no intervalo −1, − . Com efeito, note
2
que f é decrescente e g é crescente para
1,5 = 0,5 + log3 (t + 1) ⇔ t + 1 = 3 ⇔ t = 2.
Portanto, serão necessários 2 anos para que a
altura aumente de 0,5 m para 1,5 m.
b) A lei da função g pode ser escrita sob a forma
g(t) = h(3t + 2)
= 0,5 + log3 (3t + 2 + 1)
x ∈ ] − ∞, 0[. Logo, sendo f( −1) > g( −1) e
= 0,5 + log3 3 ⋅ (t + 1)
1
1
f − < g − , segue que os gráficos de f e de
2
2
= 1 + h(t).
www.soexatas.com
+
40 = 160 ⋅ 2−0,8⋅t
[04] Incorreto. Sabendo que | a | = | b | ⇒ a = ±b, vem
⇒ x = 1 ou x =
y ∈ + , então f(x) = a
x
= 0,5 + log3 3 + log3 (t + 1)
Página 4
Por conseguinte,
Resposta da questão 9:
[D]
g(t) − h(t) = 1 + h(t) − h(t) = 1,
Queremos calcular o valor de x para o qual se tem
P = 3,6. Assim,
para todo t ≥ 0.
3,6 = 0,1 + log2 (x − 1996) ⇔ x − 1996 = 23,5
Resposta da questão 6:
[A]
⇔ x = 23 ⋅ 2 + 1996
⇒ x ≅ 2007,2,
ou seja, a cidade atingiu a marca dos 3600 habitantes
em meados de 2007.
Resposta da questão 10:
02 + 04 + 08 = 14.
(01) Falso.
f(x) = 42x
2
x vértice = −
O gráfico da função y = log(x) é o que mais se
aproxima da curva considerada.
Resposta da questão 7:
[D]
Do gráfico, temos
(0, 10) ⇔ 10 = k ⋅ 2a⋅0 ⇔ k = 10
− x −1
, o mínimo da função ocorre para
b
( −1)
1
⇒ x vértice = −
⇒ x vértice = .
2a
2(2)
4
(02) Verdadeiro.
2
f(x) < 1 ⇒ 42x − x −1 < 1 ⇒ 2x 2 − x − 1 < 0
Calculando as raízes, obtemos:
1
x = −
2x 2 − x − 1 = 0 ⇒ 1
2.
x = 1
2
Estudando os sinais da função, temos:
e
(2, 20) ⇔ 20 = 10 ⋅ 2a⋅2
⇔ 2 = 22a
⇔a=
1
.
2
t
Logo, N(t) = 10 ⋅ 2 2 e, portanto, se o modelo estiver
correto, o aumento na quantidade de microorganismos entre t = 4 e t = 8 horas deve ter sido de
N(8) − N(4) = 160 − 40 = 120.000.
Resposta da questão 8:
[D]
Para t = 3,3 h sabe-se que q = 5 g. Logo,
5 = 10 ⋅ 2k⋅3,3 ⇔ 23,3k = 2−1
⇔ 3,3k = −1
⇔k=−
www.soexatas.com
10
.
33
Logo, S = x ∈
|−
1
< x < 1
2
(04) Verdadeiro.
Para x = 0, tem-se
log2 f(x) = log2 42x
2
− x −1
= log2 4 −1 = −2 .
(08) Verdadeiro.
f(x) > 8 ⇒ 42x
2
− x −1
> 8 ⇒ 4x 2 − 2x − 2 > 3 ⇒ 4x 2 − 2x − 5 > 0
Calculando as raízes, obtemos:
1 + 21
x1 =
4
4x 2 − 2x − 5 = 0 ⇒
.
1 − 21
x 2 =
4
Estudando os sinais da função, temos:
Página 5
decimal. Desse modo, m = 15,3 ⋅ 106 e
n = 1 + 0,02 = 1,02.
Portanto, o resultado pedido é:
15,3 ⋅ 106
= 15 ⋅ 106 = 1,5 ⋅ 107.
1,02
Resposta da questão 15:
06.
Logo, S = x ∈
|x<
1 − 21
1 + 21
ou x >
4
4
(16) Falso.
2
log3 f(1) = log3 42(1)
−(1)−1
q(t) = q0
⇒ 2 ⋅ q0 = q0 ⋅ q(t) = q0
3
⋅k2
⇒2
P(10)
= e10k = Q.
P0
por P(60) = P0 ⋅ ek ⋅60 .
Portanto,
3
= k2
P(60)
= e60k = (e10k )6 = Q6 .
P(0)
⇒k =34
3
Logo, q(t) = 4 t q0 .
Resposta da questão 12:
[D]
Queremos calcular o valor de t para o qual
N(t) = 7000. Logo,
t
P(10) = P0 ⋅ ek ⋅10 , supondo t em minutos. Logo,
Após 60 minutos, a população de bactérias é dada
= log3 40 = 0
Resposta da questão 11:
[E]
3
⋅k2
A população de bactérias após 10 minutos é dada por
Resposta da questão 16:
Cálculo de Juros Compostos
M → mon tan te
C → capital
M = C(1 + i)t onde
i → taxa
t → tempo
Portanto:
2000 = 1000(1 + 0,06)t ⇒ 1,06t = 2 ⇒ log2 1,06t = log2 2 ⇒ t(0,084) = 1 ⇒ t ≈ 11,9 anos
t
500 ⋅ 2 = 7000 ⇔ 2 = 14.
Portanto, como 8 < 14 < 16 ⇔ 23 < 2t < 24 , segue que
t ∈ ]3, 4[.
Resposta da questão 13:
a) Para t = ? temos P(t) = 400
Portanto:
500
1 + 22− t
= 400 ⇒ 1 + 22− t =
Resposta da questão 17:
[B]
De acordo com as informações, vem
N0
= N0 ⋅ 2k⋅10 ⇔ 210k = 2−2 ⇔ k = −5 −1.
4
500
5
1
⇒ 22− t = − 1 ⇒ 22− t = ⇒ t = 4
400
4
4
b) Para t muito grande, o valor 22−t tende a ser 0;
500
logo, P(t) será dado por P(t) =
= 500 . Portanto,
1+ 0
o número de pássaros dessa espécie se aproxima a
500.
Resposta da questão 14:
[D]
Na lei P(t) = m ⋅ nt −2011, temos que m é a população
inicial (para t = 2011) e n = 1 + i é o fator de
crescimento, sendo i a taxa de crescimento na forma
www.soexatas.com
Página 6
Baixar