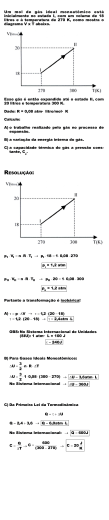
Física
Frente III
CAPITULO 4 – GASES
Volume: como um gás não possui forma
definida, o seu volume é disperso, ocupando todo o
volume disponível. Se estiver contido em um
recipiente, o volume do gás será o próprio volume do
recipiente.
Aula 09 a 11
CONCEITOS IMPORTANTES
Gás: fluido que tem forças de coesão muito fracas,
resultando em um distanciamento intermolecular
grande em comparação com sólidos e líquidos. Além
disso, possui propriedades de compressibilidade e
expansibilidade, além de ocupar todo o espaço que
lhe é oferecido.
Temperatura: como já vimos, é a medida do
grau de agitação das moléculas de um gás. Deve ser
sempre medida em Kelvin nos estudos relacionados
a gases.
Nº de mols: pode ser determinado sempre que se
souber a massa do gás - m - e a sua massa
molecular – M.
As moléculas de um gás estão em
movimentação contínua e desordenada ( o chamado
movimento
browniano),
que
só
cessaria,
teoricamente, em um estado hipotético de zero
absoluto, algo que já vimos que é impossível de ser
atingido.
Em nosso estudo passaremos a considerar
um Gás Ideal, que é um gás hipotético, cujas
propriedades não se alteram. Ele se mantém sempre
no estado gasoso e segue rigorosamente as leis de
transformações dos gases que estudaremos. Apesar
de os gases ideais se tratarem de gases fictícios, a
grande maioria dos gases reais, quando estão a
uma alta temperatura e baixa pressão, se comporta
de forma semelhante aos gases ideais ou perfeitos.
n
onde n é o n° de mols do gás
CNTP: Condições Normais de Temperatura e
Pressão. Sempre que for falado em CNTP teremos:
T = 273 K
e
P = 1 atm
Transformações Gasosas
As leis que seguem são experimentais.
Lei de Avogadro
Volumes iguais, de gases diferentes, à
mesma temperatura e pressão, contêm o mesmo n°
de moléculas.
A partir dessa lei e de experimentos chegouse ao famoso n° de Avogadro:
23
NA = 6,02x10 , que é o n° de moléculas por mol de
gás.
Se tomarmos dois gases diferentes, ou seja,
com massas molares diferentes, então a densidade
será tanto maior quanto maior a massa molar, pois:
Estudaremos nesta apostila toda a teoria que
envolve os gases ideais, mais especificamente as
suas transformações, isto é, quando um gás passa
de um estado para outro (e não é de SP para o CE
). Uma análise completa de um sistema gasoso é
determinar todas as Variáveis de Estado. São elas:
pressão, volume e temperatura (absoluta, ou seja,
em K). A massa ou o n° de mols, dependendo da
análise, também devem ser considerados.
Pressão: a pressão de um gás é a medida
do número de colisões do mesmo com as paredes do
recipiente que o contém. A definição geral de pressão
é a razão da força pela área de aplicação:
P
m
M
d
F
A
m n.M

V
V
As equações que aparecerão na sequência
são para gases ideais, entretanto, em determinadas
condições, como baixa pressão e alta temperatura o
gás real tem comportamento semelhante ao gás
ideal.
Lei de Boyle
Verificou-se que, se a temperatura T de uma
determinada massa gasosa for mantida constante, o
volume V, deste gás será inversamente proporcional
à pressão P, exercida sobre ele. Assim temos:
P1V1  P2V2  cte
Gráfico PxV da Transformação Isotérmica:
CASD Vestibulares
Gases
183
constante de proporcionalidade, foi denominada de
constante Universal dos Gases Perfeitos. Alguns
valores de R, em diferentes unidades:
R = 0,082 atm.l/mol.K
R = 8,31 J/mol.K
R = 62,3 mmHg.l/mol.K
O gráfico dessa transformação é
hipérbole equilátera, denominada isoterma.
Essa equação pode relacionar dois diferentes
estados em uma transformação gasosa qualquer,
quando não há variação de massa.
uma
Lei de Gay-Lussac
Na transformação a pressão constante de
uma dada massa gasosa, o volume é diretamente
proporcional à temperatura absoluta.
P1V1
P2V2

T1
T2
Assim:
que é a Lei Geral dos Gases Perfeitos.
V1
V
 2  cte
T1
T2
A partir da equação de Clapeyron podemos
calcular a densidade do gás:
d 
Gráfico VxT da Transformação Isobárica
PM
RT
Onde M é a massa molar do gás.
Desse modo vemos que a densidade de um
gás é diretamente proporcional à massa molecular e
à pressão e inversamente proporcional à
temperatura.
Misturas Gasosas
Fração Molar: A fração molar é um número
adimensional (sem unidade) que relaciona a parte de
uma mistura com o total. É frequentemente utilizada
para indicar a porcentagem molar de um gás em uma
mistura. Vale lembrar que a soma das frações
molares de todos os componentes de uma mistura
gasosa deve ser sempre igual a 1, ou seja, 100%.
A parte pontilhada da reta condiz com o fato
de ser impossível o estado de temperatura zero
Kelvin ou de comprimirmos um gás até ele chegar ao
volume zero.
Lei de Charles
Pressão Parcial: A pressão parcial de cada gás, em
uma mistura gasosa, é igual à pressão que o mesmo
exerceria se ocupasse o volume total da mistura
gasosa, à temperatura da mistura. Funciona como se
cada gás ignorasse a existência dos outros, só
quisesse saber dele mesmo! .
Na transformação gasosa onde não há
variação de volume chamada isocórica (ou, ainda,
isométrica ou isovolumétrica) a pressão do gás é
diretamente proporcional à temperatura absoluta.
P1
P2

 cte
T1
T2
Lei de Dalton: a pressão total da mistura gasosa é
igual à soma das pressões parciais de cada gás que
compõe a mistura.
Equação de Clapeyron
Seja uma mistura de 2 gases diferentes entre si
(ou não). Como proceder para determinar a
Pressão e/ou Temperatura final da mistura? (sem
reação química)
Com base nas leis experimentais de
Avogadro, Boyle, Charles e Gay-Lussac, Clapeyron
sintetizou-as sob a forma de uma equação de estado
de um gás ideal.
Como o volume de um gás é diretamente
proporcional ao seu n° de mols e à temperatura e
inversamente proporcional à pressão, então é natural
que:
PV
R
nT
onde
184
R,
ou
Os 2 gases, quando misturados, passam a
ocupar um volume total VF (que pode ou não ser a
soma dos volumes iniciais de cada gás, dependendo
do problema), estando a uma temperatura final TF e
uma pressão final PF. A única coisa que podemos
garantir que não vai mudar após a mistura dos dois
gases é o número de mols. O número de mols da
mistura será a soma dos números de mols de cada
gás separadamente (Lembra-se da Lei de Lavoisier
de conservação da matéria? ). Assim:
PV  nRT
a
Gases
CASD Vestibulares
PFVF
PV P V
 nF  n1  n2  1 1  2 2
RTF
RT1 RT2
Ou seja:
PFVF P1V1 P2V2


RTF
RT1 RT2
03. Dois litros de um gás encontram-se a 27ºC, sob
600 mmHg de pressão. Qual será a nova pressão do
gás, a 127ºC, com volume de 10 litros?
Resolução:
Teoria Cinética dos Gases
As leis anteriormente estudadas para gases
perfeitos são o resultado de estudos macroscópicos.
A Teoria Cinética dos Gases busca, através de um
estudo microscópico, interpretar o comportamento
dos gases. Ela se baseia em um modelo de gás
ideal, que é definido por algumas hipóteses. São
elas:
04. Seja um balão A que tem o quádruplo da
capacidade de um balão B. Ambos os balões contém
o mesmo gás à mesma temperatura. A pressão no
balão A é de 2 atm e no balão B é de 8 atm. Calcule
a pressão após a abertura da torneira, de forma a
não variar a temperatura.
1. O gás é constituído por um número muito grande
de moléculas em movimento desordenado descrito
pelas leis de Newton.
2. O volume de cada molécula é desprezível se
comparado ao volume do recipiente.
B
3. As forças intermoleculares (atração e repulsão
entre as moléculas do próprio gás) são desprezíveis,
exceto nas colisões mútuas e com as paredes do
recipiente.
4. As colisões são 100% elásticas (ou seja,
conservam a energia) e de duração desprezível.
A
Resolução:
Partindo desses postulados e em vista dos
princípios da Mecânica Newtoniana (a que vocês
estudam com o Paulinho ) é possível provar que a
energia cinética média das moléculas, introduzindo a
constante de Boltzmann (k):
EC 
R
Onde k 
NA
3
kT
2
Exercícios Resolvidos
.
01. Um reservatório de 30 litros contém nitrogênio, no
estado gasoso (diatômico, ou seja, N2), à temperatura
de 20ºC e à pressão de 3 atm. A válvula do
reservatório é aberta momentaneamente e uma certa
quantidade de gás escapa para o meio ambiente,
fazendo com que a pressão do gás restante no
reservatório seja de 2,4 atm. Determine a massa do
nitrogênio que escapou.
Dados: R = 0,082 atm;l/mol.K;
= 28 g/mol
Resolução:
Exercícios de Sala
01. 10 litros de um gás perfeito encontram-se sob
pressão de 6 atm e à temperatura de 50ºC. Ao sofrer
uma expansão isotérmica, seu novo volume passa a
15 litros. Calcule a nova pressão.
Resolução:
Da equação de Estado, obtemos: n 
PV
RT
Como V e T permanecem constantes, temos que n é
diretamente proporcional a P. Assim:
02. Determine a temperatura de um gás, sabendo
que 2 mols desse gás ocupam um volume de 100
litros à pressão de 0,82 atm. Dado: R = 0,082
atm.l/mol.K
n2 P2
n
2, 4

 2 
 n2  0,8n1
n1 P1
n1 3,0
(I)
Resolução:
CASD Vestibulares
Gases
185
Mas como
n1 
 P0  P  .S.( L0  x )  RT
P1V
3.30
 n1 
RT
0,082.293
Fazendo (II) em (III), temos:
Isto é: n1  3,7 mols Então, substituindo em (I),
kx 

 P0 
 .S.( L0  x )  RT
S 

obtemos:
n2  0,8.3,7  n2  2,9 mols
Multiplicando termo a termo, obtemos:
O número de mols que deixou o recipiente foi
P0SL0  P0Sx  kxL0  kx 2  RT (IV)
n  3,7  2,9  n  0,8 mol
Fazendo (I) em (IV) para aparecer T0:
Como a massa molecular do nitrogênio diatômico
(N2) é M = 28 g/mol, temos que a massa que
escapou é:
RT0  P0Sx  kxL0  kx 2  RT
Dividindo por R e fatorando, achamos:
m  n.M  n  0,8.28

(III)
T  T0 
m  22, 4 gramas
x
 P0S  kL0  kx 
R
Exercícios
02. (Questão avançada) Um mol de gás perfeito está
contido em um cilindro de secção S fechado por um
pistão móvel, ligado a uma mola de constante
elástica k. Inicialmente, o gás está na pressão
atmosférica P0 e temperatura T0, e o comprimento do
trecho do cilindro ocupado pelo gás é L0, com a mola
não estando deformada. O sistema gás-mola é
aquecido e o pistão se desloca de uma distância x.
Equações Necessárias
Pressão: P 
F
A
Lei de Boyle: P1V1  P2V2
V1 V2

T1 T2
P
P
Lei de Charles: 1  2
T1 T2
PV
PV
Lei Geral dos Gases Ideais: 1 1  2 2
T1
T2
Equação de Estado: PV  nRT
Lei de Gay-Lussac:
Denotando a constante de gás por R, a nova
temperatura do gás é?
Resolução:
Na situação inicial aplicando a equação de Clapeyron
para 1 mol de gás, obtemos:
Pressão em um líquido: P2  P1 
O volume inicial é igual à área da seção vezes o
comprimento inicial. Assim:
Força Elástica: Felástica  kx
Força de Atrito: Fatrito 
P0V0  RT0
V0  SL0  P0SL0  RT0
Fmola  Fgás
Da definição de pressão:
F
F
P   P 
 Fgás  P.S
S
S
kx
S
N
 Nível 1
01. (UNIVALI-SC) O comportamento de um gás real
aproxima-se do comportamento de gás ideal quando
submetido a:
a) baixas temperaturas e baixas pressões.
b) altas temperaturas e altas pressões.
c) baixas temperaturas independentemente da
pressão.
d) altas temperaturas e baixas pressões.
e) baixas temperaturas e altas pressões.
(I)
Na situação final, a força aplicada pela mola deve
equilibrar o acréscimo de força do gás (devido ao
aumento da pressão).
kx  P.S  P 
 g h21
02. (UFU-MG) As grandezas que
completamente o estado de um gás são:
a) somente pressão e volume.
b) apenas o volume e a temperatura.
c) massa e volume.
d) temperatura, pressão e volume.
e) massa, pressão, volume e temperatura.
(II)
Aplicando Clapeyron para a situação final, vem:
PV  RT
A pressão e o volume finais são dados por:
P  P0  P e V  S.( L0  x )
definem
Assim, a equação de Clapeyron fica:
186
Gases
CASD Vestibulares
03. (MACK) Se a pressão de um gás confinado é
duplicada a temperatura constante, a grandeza do
gás que duplicará será:
a) a massa
b) a massa específica
c) o volume
d) o peso
e) a energia cinética
09. (UFPE) Uma certa quantidade de gás ideal ocupa
30L à pressão de 2atm e à temperatura de 300K.
Que volume passará a ocupar se a temperatura e a
pressão tiverem seus valores dobrados?
a) 7,5L
b) 15L c) 30L d) 60L e) 120L
10. (UNB) Considere n mols de um gás ideal,
monoatômico, encerrado num recipiente de volume V
onde a pressão é p e a temperatura, medida em
graus Celsius é T. Marque o item que traz a relação
correta. Nessas relações: E = energia cinética média
das moléculas do gás; NA = n° de Avogadro; R =
constante universal dos gases ideais; K = constante
de Boltzmann.
a) pV = nNaKT
b) pV = NART
c) pV = 2nNAE/3
d) pV/NA =nKT +273nK
04. (UFU-MG) Um recipiente rígido de volume 4,1
litros é dotado de uma válvula de segurança, cuja
abertura ocorre quando a pressão interna atinge 40
atm. Se o recipiente contém 5 mols de um gás
perfeito, a máxima temperatura no seu interior é:
(Dado: R = 0.082 atm L/mol K)
0
0
0
a) 127 C
b) 277 C
c) 473 C
0
0
d) 527 C
e) 649
11. (CEFET) O reservatório representado contém
3
05. (AMAN) Um gás perfeito se encontra em um
recipiente de 4L de volume sob pressão de 2 atm e a
uma temperatura de 27° C. O gás é então
comprimido, sob pressão constante até que seu
volume seja reduzido a 25 % do inicial. Em seguida,
o gás é aquecido a volume constante, até uma
temperatura de 477° C. A pressão do gás, no seu
estado final, valerá:
a) 10 atm b) 8 atm c) 12 atm d) 15 atm e) 20 atm
0,249 m de um gás perfeito a 27° C e se comunica
com um manômetro de tubo aberto que contém
mercúrio. Sabe-se que a pressão atmosférica no
local vale 680 mmHg, que a constante dos gases
–1 –1
5
vale 8,30 J.mol .K e que 1x10 Pa corresponde a
760 mmHg. Desconsiderando o volume do
manômetro é possível afirmar que existem no
reservatório:
a) 5 mols de gás.
b) 36 mols de gás.
c) 8 mols de gás.
4
d) 3x10 mols de gás.
e) 22 mols de gás.
06. (UERJ) Para podermos aplicar a equação PV =
nRT dos gases perfeitos, indicamos P em
atmosferas, V em litros e T em Kelvin. Assim,
devemos utilizar para R o valor numérico:
a) 273/22,4
b) 22,4/273
c) 1/22,4
d) 1/273
e) 273
07. (CEFET) Um gás, contido em um cilindro, à
pressão atmosférica, ocupa apenas a metade de seu
volume à temperatura ambiente. O cilindro contém
um pistão, de massa desprezível, que pode mover-se
sem atrito. Esse gás é aquecido, fazendo com que o
pistão seja empurrado, atingindo o volume máximo
permitido. Observa-se que a temperatura absoluta do
gás é aumentada em 3 vezes do seu valor inicial. Na
situação final, a pressão do gás no cilindro deverá
ser:
a) 1/3 da pressão atmosférica.
b) igual à pressão atmosférica.
c) 3 vezes a pressão atmosférica.
d) 1,5 vezes a pressão
atmosférica.
e) 4 vezes a pressão atmosférica.
12. (FUVEST) Um cilindro contém certa massa M0 de
um gás a T0 = 7 ºC (280 K) e pressão P0. Ele possui
uma válvula de segurança que impede a pressão
interna de alcançar valores superiores a P0. Se essa
pressão ultrapassar P0, parte do gás é liberada para
o ambiente. Ao ser aquecido até T = 77 ºC (350 K), a
válvula do cilindro libera parte do gás, mantendo a
pressão interna no valor P0. No final do aquecimento,
a massa de gás que permanece no cilindro é,
aproximadamente, de:
a) 1,0 M0
b) 0,8 M0
c) 0,7 M0
d) 0,5 M0
e) 0,1 M0
13. (PUCCAMP) Um gás perfeito é mantido em um
cilindro fechado por um pistão. Em um estado A, as
suas variáveis são: PA = 2,0 atm; VA = 0,90 litros; TA
0
= 27 C. Em outro estado B, a temperatura é T B = 127
0
C e a pressão é PB = 1,5 atm. Nessas condições, o
volume VB, em litros, deve ser:
a) 0,90
b) 1,2
c) 1,6
d) 2,0
e) 2,4
08. (CEFET) Numa transformação gasosa cíclica, em
forma de quadrado de lados paralelos aos eixos de
um gráfico da pressão absoluta de um gás, em
função de seu volume gasoso, podemos afirmar que
ela apresenta:
a) duas transformações isobáricas e duas isométricas.
b) duas transformações isotérmicas e duas isométricas.
c) duas transformações adiabáticas e duas isométricas.
d) duas transformações adiabáticas e duas isobáricas.
e) duas transformações isobáricas e duas adiabáticas.
CASD Vestibulares
14. (UNISA-SP) Um volume de 8,2 litros é ocupado
0
por 64g de gás oxigênio à temperatura de 27 C.
Qual é a pressão no interior do recipiente? Considere
o oxigênio um gás perfeito. (1 mol de O2 = 32g) (R =
0,082 atm L/mol.K)
a) 2,0 atm
b) 3,0 atm
c) 4,0 atm
d) 6,0 atm
e) 8,0 atm
Gases
187
15. (FUVEST) Certa massa de gás ideal sofre uma
compressão isotérmica muito lenta passando de um
estado A para um estado B. As figuras representam
diagramas PxT e VxT, sendo T a temperatura
absoluta, V o volume e P a pressão do gás. Nesses
diagramas, a transformação descrita acima só pode
corresponder às curvas:
a) I e IV
d) I e VI
b) II e V
e) III e VI
b) Sendo p2 a pressão final no frasco 2 e p3 a
pressão final no frasco 3 qual será o valor da relação
p2/p3, ao final do experimento?
Observação: Desprezar o volume dos tubos das
conexões.
c) III e IV
16. (FUVEST) O gasômetro G, utilizado para o
armazenamento de ar, é um recipiente cilíndrico,
metálico, com paredes laterais de pequena
espessura. G é fechado na sua parte superior, aberto
na inferior que permanece imersa em água e pode se
mover na direção vertical. G contém ar, inicialmente à
temperatura de 300K e o nível da água no seu interior
se encontra 2,0m abaixo do nível externo da água.
Nessas condições, a tampa de G está 9,0m acima do
nível externo da água como mostra a figura a seguir.
Aquecendo-se o gás, o sistema se estabiliza numa
nova altura de equilíbrio, com a tampa superior a uma
altura H, em relação ao nível externo da água, e com
a temperatura do gás a 360K. Supondo que o ar se
comporte como um gás ideal, a nova altura H será,
aproximadamente, igual a:
02. (FUVEST) Um cilindro de oxigênio hospitalar (O2),
de 60 litros, contém, inicialmente, gás a uma pressão
de 100 atm e temperatura de 300 K. Quando é
utilizado para a respiração de pacientes, o gás passa
por um redutor de pressão, regulado para fornecer
gás oxigênio a 3 atm, nessa mesma temperatura,
acoplado a um medidor de fluxo, que indica, para
essas condições, o consumo de oxigênio em
litros/minuto. Assim, determine:
a) O número n0 de mols de O2, presentes
inicialmente no cilindro.
b) O número n de mols de O2, consumidos em 30
minutos de uso, com o medidor de fluxo indicando 5
litros/minuto.
c) O intervalo de tempo t, em horas, de utilização do
O2, mantido o fluxo de 5 litros/minuto, até que a
pressão interna no cilindro fique reduzida a 40 atm.
Note e Adote:
Considere o O2 como gás ideal.
Suponha a temperatura constante e igual a 300K
-2
R = 8x10 litros.atm/K
a) 8,8m
b) 9,0m c) 10,8m d) 11,2m
03. (FUVEST) Um mol de gás ideal é levado
lentamente do estado inicial A ao estado final C,
passando pelo estado intermediário B. A Figura 1
representa a variação do volume, V do gás, em litros
(L), em função da temperatura absoluta T, para a
transformação em questão. A constante dos gases
vale R=0,082 atm.L./(mol.K).
a) Dentre as grandezas pressão, volume e
temperatura, quais permanecem constantes no
trecho AB? E no trecho BC?
b) Construa na Figura 2 o gráfico da pressão P em
função da temperatura absoluta T. Indique
claramente os pontos correspondentes aos estados
A, B e C. Marque os valores da escala utilizada no
eixo da pressão P.
c) Escreva a função P(T) que representa a pressão P
do gás em função da temperatura absoluta T, no
intervalo de 300K a 600K, com seus coeficientes
dados numericamente.
e) 13,2m
 Nível 2 - Aprofundamento
01. (UNICAMP) O esquema abaixo representa um
dispositivo para se estudar o comportamento de um
gás ideal. Inicialmente, no frasco 1, é colocado um
gás à pressão de 1 atmosfera, ficando sob vácuo os
frascos 2 e 3. Abre-se, em seguida, a torneira entre
os frascos 1 e 2 até que se estabeleça o equilíbrio.
Fecha-se, então, esta torneira e abre-se a torneira
entre os frascos 1 e 3. O volume do frasco 1 é 9
vezes maior do que o do frasco 2 e o do 3 é 9 vezes
maior que o do 1.
a) Feito o procedimento acima descrito, em que
frasco haverá menor quantidade de moléculas do
gás? Justifique.
188
Gases
CASD Vestibulares
05. (ITA) Um recipiente continha, inicialmente, 10,0
6
2
kg de gás sob a pressão de 10.10 N/m . Uma
quantidade m de gás saiu do recipiente sem que a
temperatura variasse. Determine m, sabendo que a
6
2
pressão caiu para 2,5.10 N/m .
a) 2,5 kg b) 5,0 kg c) 7,5 kg d) 4,0 kg e) 2,0 kg
06. (ITA) Na figura abaixo, uma pipeta cilíndrica de
25 cm de altura, com ambas as extremidades
abertas, tem 20 cm mergulhados em um recipiente
com mercúrio. Com sua extremidade superior tapada,
em seguida a pipeta é retirada lentamente do
recipiente. Considerando uma pressão atmosférica
de 75 cm Hg, calcule a altura da coluna de mercúrio
remanescente no interior da pipeta.
04.
(FUVEST) Um compartimento cilíndrico, isolado
termicamente, é utilizado para o transporte entre um
navio e uma estação submarina. Tem altura
2
H0 = 2,0 m e área da base S0 = 3,0 m . Dentro do
compartimento, o ar está inicialmente à pressão
atmosférica (Patm) e a 27°C, comportando-se como
gás ideal. Por acidente, o suporte da base inferior do
compartimento não foi travado e a base passa a
funcionar como um pistão, subindo dentro do cilindro
à medida que o compartimento desce lentamente
dentro d’água, sem que ocorra troca de calor entre a
água, o ar e as paredes do compartimento. Considere
a densidade da água do mar igual à densidade da
água. Despreze a massa da base. Quando a base
inferior estiver a 40 m de profundidade, determine:
a) A pressão P do ar, em Pa, dentro do
compartimento.
b) A altura H, em m, do compartimento, que
permanece não inundado.
c) A temperatura T do ar, em °C, no compartimento.
Curvas PxV para uma massa de ar que, à Patm e
3
27ºC, ocupa 1 m : (A) isobárica, (B) isotérmica, (C)
sem troca de calor, (D) volume constante. Patm = 105
2
Pa ; 1 Pa = 1 N/m
07.
(ITA) Um tubo capilar fechado em uma
extremidade contém uma quantidade de ar
aprisionada por um pequeno volume de água. A
7,0°C e à pressão atmosférica (76,0 cmHg) o
comprimento do trecho com ar aprisionado é de
15,0 cm. Determine o comprimento do trecho com ar
aprisionado a 17,0°C. Se necessário, empregue os
seguintes valores da pressão de vapor da água: 0,75
cmHg a 7,0°C e 1,42 cmHg a 17,0°C.
08. (ITA) Um tubo capilar de comprimento 5a é
fechado em ambas as extremidades. Ele contém ar
seco, que preenche o espaço no tubo não ocupado
por uma coluna de mercúrio de densidade ρ e
comprimento a. Quando o tubo está na posição
vertical, as colunas de ar têm comprimentos a e 3a.
Nessas condições calcule a pressão no tubo capilar
quando em posição horizontal.
CASD Vestibulares
Gases
189
14. (Superdesafio) Na metade de um tubo de
comprimento L, colocado horizontalmente e fechado em
ambos os extremos, encontra-se uma coluna de
mercúrio de comprimento l. Se colocarmos o tubo na
posição vertical, então, a coluna de mercúrio desloca-se
à distancia Δl da sua posição inicial. A que distância, do
meio do tubo, ficará o centro da coluna, se abrirmos um
dos extremos do mesmo na posição horizontal (1)? Se
abrirmos o extremo superior do tubo na posição vertical
(2)? Se abrirmos o extremo inferior do tubo na posição
vertical (3)? A pressão atmosférica é igual a H cmHg. T
é constante.
09. (IME) Dois recipientes, condutores de calor, de
mesmo volume, são interligados por um tubo de volume
desprezível e contêm um gás ideal, inicialmente a 27°C
e 1,5.105 Pa. Um dos recipientes é mergulhado em um
líquido a 127°C enquanto que o outro, simultaneamente,
é mergulhado em oxigênio líquido a -173°C. Determine a
pressão de equilíbrio do gás.
Gabarito
Nível 1
1. d 2. d 3. b 4. a 5. e 6. b 7. d 8. a 9. c
10. d 11. a 12. b 13. c 14. d 15. c 16. d
10. (OBF) A densidade do ar a 27°C ao nível do mar é
aprox. 1,2 kg/m3. Calcule, ao nível do mar:
a) A densidade do ar a 127°C.
b) O volume de um balão de plástico de massa 600g
para que ele flutue com ar a 127°C e a temperatura
ambiente de 27°C.
Nível 2
1. a) Frasco 1
b) 10
2. a) n0 = 250 mols b) n = 18,75 mols
c) 4 horas
3. a) AB – pressão; BC – Volume
b) Gráfico
c) P(T) = 1+ T  300
300
4. a) P = 5.105 Pa b) H = 0,6m c) T = 177° C
5. c
6. h = 18,4cm
7. L = 15,7 cm, pois Patm = Pvapor + Par
8. P0 = 3ρga/4
9. P = 1,25.105 Pa
10. a) d = 0,9 kg/m3
b) V = 2 m3
11. a) Lf = 14 cm
b) Tf = 840 K
12. a) Ptotal = Pp + Patm ; Ptotal = 3,0 atm
b) m = 3,25 g
13. L = 764 mm
14. 1) Pressão inicial no tubo:
l l
l 
P0    0   onde ρ é a densidade do
2  l l0 
mercúrio (veja exercício 8 do nível 2)
A coluna de mercúrio vai se deslocar de:
l.l0  2H  l0 l   onde l   L  l  2
0
11. (OBF) Um gás ideal, inicialmente à temperatura T0 =
27°C, é confinado em um recipiente horizontal cilíndrico
de comprimento inicial L0 = 10 cm (ver figura). À tampa
do recipiente é presa uma mola de constante elástica k
= 100 N/m, inicialmente comprimida de x0 = 4 cm, que
se encontra conectada a um bloco de massa m = 1 kg
em repouso. O coeficiente de atrito estático entre o
bloco e a superfície vale μe = 0,8. Uma chama aquece o
gás, que então se expande lentamente e a velocidade
constante, aumentando o comprimento do recipiente.
Despreze o atrito da tampa com as paredes do
recipiente. Quando o bloco encontrar-se na iminência de
movimento, calcule:
a) o comprimento do recipiente;
b) a temperatura do gás.
l1 
O mercúrio não derrama se:
12. (OBF) Colocam-se 3 litros de água numa panela de
pressão de 5 litros (volume total). O orifício de escape
de vapor da panela tem diâmetro 2,83 mm e o “pesinho”
para regular pressão tem massa 126 g. A pressão
atmosférica é a normal (1 atm).
a) Calcular a pressão total na panela em regime normal
de funcionamento.
b) Se a temperatura da água no regime normal é 127°C,
calcular a massa de gás na panela.
2
l0
H
H 
   1 
l
l
l
 
2) A coluna de mercúrio vai se deslocar de:
 2H  l0 l 

l.l0
l 2 
     2

2  H  l   l

l
l
0 


O mercúrio não derrama se:
l0

l
13.
Um
barômetro
dá
indicações
falsas
como
conseqüência da presença de
uma pequena quantidade de ar
sobre a coluna de mercúrio.
Para uma pressão px1 = 755
mmHg, o barômetro indica p1 =
748 mmHg e para px2 = 740
mmHg temos p2 = 736 mmHg.
Encontre o comprimento L do
tubo do barômetro, mostrado na
figura 1.
190
   

2H  l
 l l0  
 2 H  l  
2 H  l 

 1 
l
l


2
3) A coluna de mercúrio vai se deslocar de:
l 3 
 2H  l0 l 

l.l0
     2

2  H  l   l

l
l

0 

O mercúrio não derrama se:
4 H  l 
2 H  l 
l0

1 
l
l2
l
2
Gases
CASD Vestibulares