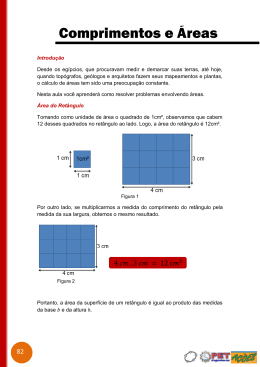
ALUNO (A):
SÉRIE:
Nº:
TURMA:
DISCIPLINA: MATEMÀTICA-D4 - 4
DATA:
Professor: VALDEMIRO
Estamos retomando a questão apresentada anteriormente para, agora, dar os passos fundamentais
da nossa proposta pedagógica deste ano.
Tomando, como exemplo, mais uma vez a questão que apareceu no Vestibular da PUC - 2000, a
título de ilustração, em nível de matemática pura, formularam: "ABCD é um retângulo, no qual, AB =
20m e BC = 15m; M é um ponto de AB tal que MA = 4m. Calcular a área do paralelogramo inscrito no
retângulo ABCD, sabendo que tem um vértice no ponto M e que os seus lados são paralelos às diagonais
de retângulo ABCD.
Respostas: A) 72m2; B)80m2; C) 88m2;
A
M
B
D)96m2;
E)104m2.
D
C
Ora, uma questão dessas, da maneira como foi apresentada, não passa além da utilização do
conhecimento matemático puro, ou seja, possivelmente, a resolução de muitos, foi feita por lógica ou,
então, não se passou além de algum domínio da geometria plana. Mas, afinal, resolvido a questão e a
resposta obtida, tudo o que aconteceu, igualmente, não deve ter passado, apenas, de um conhecimento
mecânico, abstrato e/ou de cálculos até obter um número qualquer e, nada mais natural do que nos
indagar, qual foi o sentido prático disto? Lembramos que isto também é matemática e se faz necessário.
Diante deste questionamento, então, chegaríamos ao segundo tipo de matemática e que para
muitos professores, alunos, pais e comunidade em geral é a que perguntam, ou seja, e a matemática não
deveria ser aplicada?
Poderíamos pensar o mesmo problema, porém com um sentido mais prático, cotidiano, ou seja,
algo mais real, da nossa vida. Muitas poderiam ser as situações reais se todos nós soltássemos a nossa
imaginação. Uma muito comum, seguindo a matemática convencional e apresentada, com freqüência, em
livros textos nas escolas, poderia ser a formulação que utilizaria os mesmos dados alertando apenas que o
retângulo é um terreno de uma pessoa e que o paralelogramo será a área de construção de uma casa, por
exemplo. Por isto, deseja-se saber a área construída e cada uma das áreas ainda ociosa.
Temos, freqüentemente, alertado que, neste segundo caso, a matemática é, na verdade, um
pensamento que denominamos de utilidade, ou seja, na prática, a pessoa deseja construir uma casa num
terreno e necessita realizar os cálculos para determinar a área do seu interesse e, por isto, é uma
matemática que chamamos de utilitarista.
Contudo, segundo um pensamento de uma escola jesuítica, isto é necessário, mas ainda não é o
suficiente, pois o conhecimento deve estar a serviço de outras finalidades. Para compreender isto um
pouco melhor, vamos usar o livrinho das Características da Educação da Companhia de Jesus, entre tantas
orientações, no item 149, neste é afirmado à necessidade da "inserção na realidade concreta" e, também,
no item 162, afirma-se que "a pedagogia deve incluir a análise, a reflexão ativa e a síntese".
Partindo, diante disto, para uma Pedagogia do Colégio ou uma Proposta de Educação Matemática
por nós imaginada e devidamente planejada para esta Série, precisamos ingressar, enfim, na matemática
que nós chamamos de reflexiva, ativa e crítica. Afinal, então, o que se entende quando se afirma uma
matemática reflexiva e crítica?
A proposta que apresentamos, por exemplo, no nosso Planejamento, é que, a matemática, além do
conhecimento puro e aplicativo prático, ele também seja significativo, ou seja, que o problema, no
mínimo seja de uma realidade concreta do contexto, especialmente, do humano onde fazer significado
representa que seja promovida a vida humana. Conforme as Características da Companhia de Jesus, mais
uma vez, citando o item 84 deste documento, que se tenha "uma preocupação especial pelos pobres". Nós
diríamos hoje: Por pobres se entende como sendo todos aqueles que estão excluídos da sociedade e que
esta deveria ser o enfoque nesta formulação de problema matemático.
Portanto, utilizando o mesmo problema, teríamos que localizá-lo, dentro do que pensamos como
Educação diferenciada e importante nesta Escola, num contexto bem mais real onde sejam comparadas
situações de estilo de vida de pessoas. Aqui vai da imaginação, da percepção da pessoa, do professor, no
caso, para criar uma situação problema. Um paralelogramo inscrito num retângulo, tal como aparece na
questão do vestibular da Puc, permite inúmeras situações. Cada pessoa, por exemplo, poderá dar sua idéia
e sugestão. Algumas serão bastante óbvias numa matemática apenas aplicada e, outros, irão conseguir
propor situações mais significativas com uma visão de mundo que permite refletir, analisar e criticar.
Não é preciso pensar muito e perceber que houve um êxodo de pessoas do meio rural para o
urbano. Pela propaganda feita da cidade de Curitiba, há, sem dúvida, a vinda de um enorme contingente
de pessoas e, o aglomerado destas, nas mais variadas formas. Assim, redimensionando o problema,
imaginamos a mesma situação gráfica, porém, redimensionando as medidas, estas deveriam ser
ampliadas, ou seja, multiplicadas por 10 e na mesma unidade de medida de modo que o retângulo
represente, hipoteticamente, uma quadra de 200m por 150m e o segmento AM tendo 40m. Faça, então,
agora, numa folha para ser entregue, uma figura mostrando estes dados e as demais solicitações que virão
em seguida.
Agora, como conteúdo novo e, também, diante do que chamamos de pensamento complexo, ou
seja, a formulação de inúmeros e variados questionamentos, queremos ampliar a capacidade de análise
dos alunos por meio dos questionamentos que o professor fará na recriação desta questão.
Vamos localizar no paralelogramo os vértices M (já apareceu antes), N, O e P. O ponto N está no
segmento BC. Já o O está no CD e o P está no AD. Já AB, BC, CD e AD são ruas da quadra. A área das
figuras geométricas AMP denominamos de 1. Já MBN de 2, a NCO de 3 e, finalmente, a ODP de 4.
Coloque estas informações todas na figura da sua folha e, em seguida, faça os cálculos das áreas.
Se a Prefeitura de Curitiba, por exemplo, desejasse construir uma rua ligando MO ou NP elas
seriam iguais e, eventualmente, quais as medidas de cada (questão levantada na folha anterior)? O
paralelogramo MNOP é retângulo? As diagonais AC e BD se encontrariam no mesmo ponto com as
diagonais MO e NP ? Faça também estes cálculos na sua folha.
Por último, tomando um aspecto mais consciente e crítico, imaginamos que 1 seja a favela
MALMEQUER. Esta foi conquistada pela luta e, finalmente, pela invasão. Devido à organização do
grupo e a formação de uma comissão de moradias, ficou definido que a favela teria 50 áreas iguais.
Também ficou estabelecido que cada barraco deveria ter, em média, 4 pessoas. Já o 2 representa o
Conjunto Residencial CLASSE MÉDIA, com 30 sobrados, todos utilizando áreas iguais do terreno e com
uma média de 3 pessoas por residência. O 3 é o bosque Ecológico RUBINSKY. No 4 está localizado a
Residência dos TAKOCUCHA e onde só há duas pessoas. O paralelogramo MNOP, finalmente, pertence
ao especulador latifundiário MILIONARIOZÃO. Como você já calculou cada área antes e, agora, diante
do tipo de uso do solo como fica a área de cada uma delas e que chamamos de 1, 2, 3, 4 e MNOP? Qual a
área estipulada por pessoa em cada região apresentada? Faça tudo isto na sua folha, enfim.
Iniciamos, perguntando pela ocupação do solo, ou seja, quantos metros quadrados caberiam a
cada pessoa em cada uma destas diferentes figuras excluindo, é claro, o número 3 ( transdisciplinar ).
Aqui, também, caberia perguntar-se pela quantidade de sem-tetos na cidade de Curitiba, ou seja, pessoas
com área zero. Vale à pena pesquisar isto. A construção da estrada poderia ser do interesse de algum
grupo destes das diferentes figuras? Se o terreno do paralelogramo, para fins sociais, fosse expropriado
por esta Prefeitura e usado, ao invés de alguma rua, para a construção de um prédio de 10 andares iguais,
com cerca de 30 metros de altura, com 40 apartamentos iguais por andar e uma média de 5 pessoas por
apartamento, então como ficaria a área lateral, total e volume e qual o número de habitantes por prédio de
um prisma formado ( usando a geometria espacial ) tendo como base o paralelogramo onde MN e OP são
dois lados e os outros dois são formados pela menor distância do vértice M até o lado OP e do vértice O
até o lado MN ( mostra conteúdos cumulativos ). Qual a área não ocupada deste paralelogramo MNOP?
Qual a área, em média, para cada pessoa ? Que solução foi dada ao problema habitacional? Responda
tudo isto novamente na sua folha...
Finalmente, ainda deveríamos nos perguntar: Quantas outras perguntas interessantes e importantes
este problema permitiria formular?
Será que, à medida que este problema original da PUC foi sofrendo as modificações feitas, estas
passaram a enfocar a questão da exclusão ou da inclusão social?
Agora, como aluno, que pergunta questionadora você faria para este problema da Puc? Que
reflexão importante você acha que deveria ser levantada? Apresente esta análise no final da sua folha
onde você resolveu todos os desafios apontados anteriormente.
Apresentamos, nesta proposta, algumas idéias. Foram pensadas ruas, moradias, prédios, favela,
enfim, áreas 1, 2, 3, 4 e MNOP com pessoas nestes locais e, principalmente, a existência, também em
Curitiba, de sem-tetos. Será que não teríamos saídas diferentes e melhores das apresentadas para
resolvermos o problema habitacional para a cidade de Curitiba? Que solução(ões) mais racional(ais) você
apresentaria incluindo, especialmente, a problemática dos sem tetos ou todas as moradias mais precárias
ainda existentes na Capital Ecológica ? Talvez seja importante lembrar que as questões de habitação não
vem isolada, mas vem associadas a questões econômicas também. Sendo este, portanto, outro fator
essencial que deveria ser levantado e refletido.
Gostaríamos de lembrar que da formulação de um problema fechado, em matemática, do
vestibular da PUC, terminamos com uma série de perguntas bastante abertas e que, certamente, exige uma
capacidade de um pensamento racional, levando para uma situação com complexidade e com soluções
variadas.
Para concluir, finalmente, fica em aberto para que cada leitor, em especial, segundo sua
experiência de vida e seu modo próprio de pensar, quem sabe, também, poderia contribuir com inúmeros
questionamentos e perguntas interessantes que transformaria este simples problema em uma riqueza ainda
maior de reflexão crítica. É para isto que o convidamos estimado leitor ( objetivo de aprofundamento do
problema ).
Enfim, nos parece que, este problema mostrou, apesar de, talvez, ainda bastante restrito, uma nova
visão de educação e de construção de conhecimento em matemática. O grande mérito e desejo é que o
Ensino possa realmente formar sujeitos com excelência acadêmica ( obtido pelo estudo dos conteúdos
formais = matemática pura ) e com excelência humana ( obtido pela matemática aplicada a realidade, seja
de forma útil, mas, principalmente, ampliando o pensamento e tornando o sujeito como um ser reflexivo
para que possa tornar-se um cidadão consciente e tenha possibilidades de intervir na sociedade com maior
competência ). Este será o tom do nosso trabalho no primeiro semestre. Maiores detalhamentos virão nas
próximas aulas.
Professor, Valdemiro Ruppenthal
Em seguida aparece uma resolução interessante de um aluno do Terceiro Ano EM – 2011.
200 m
A
3
0
m
M
B
A²
1 X³
2
P
0
25
1
5
0
m
N
X²
m
5
A¹
3
4
X¹
O
D
40 m
X¹) 200 = 150
40
x¹
200X¹ = 6000
x¹ = 6000
200
X²) x² = 120² + 160²
x² = 14400 + 25600
x = √ 40000
x = 200 m
x¹ = 30 m
X) - x² = 200² + 150²
x² = 40000 + 22500
x = √ 62500
x = 250 m
X³) x² = 30² + 40²
x² = 900 + 1600
x = √ 2500
x = 50 m
A¹) b x h = 40 x 30 = 1200 = 600 m²
2
2
2
A²) b x h = 120 x 160 = 19200 = 9600 m²
2
2
2
C

Área do Paralelogramo
Ap) 30000 – (600 x 2 + 900 x 2)
30000 – 20400
9600 m²
Área: 9600 m²

Distribuição dos territórios
1. Malmequer : (50 áreas iguais; 4 pessoas por barraco)
A) 600 = 12 m² por barraco / 12 m² = 3 m² por pessoa
50
4
2. Conjunto Residencial classe média : (30 sobrados; 3 pessoas por residência)
A) 9600 = 320 m² por residência / 320 = 106,7 m² por pessoa
2
3
3. Bosque Ecológico Rubinsky
O bosque ecológico Rubinsky está localizado numa área de 600 m², como uma área de
preservação ambiental.
4. Família Tokochuca
A) 9600 = 4800 m² por pessoa ( *apenas 2 pessoas)
2
5. Milionariozão: (especulador latifundiário)
Ele possui uma área de aproximadamente 9600 m²

Com os cinco exemplos acima podemos observar o problema da divisão de terras entre
a população, o que favorece a exclusão social. Se pegarmos a grande extensão
territorial, numa situação hipotética, pertencente ao Milionariozão de aproximadamente
9600 m², podemos propor uma solução para essa situação – problema.
Se o terreno do Paralelogramo, para fins sociais, fosse expropriado pela
prefeitura e usado, ao invés de alguma rua, para a construção de um
prédio de dez andares iguais, com quarenta apartamentos iguais por
andar e uma média de cinco pessoas por apartamento, a área lateral,
total, volume e o número de habitantes por prédio ficaria assim:

Construção do prédio na área MNOP
Largura: 20 m
Comprimento: 20 m
área total do terreno: 9600 m²
Altura: 30 m
Área lateral: 20 x 30 x 4 = 2400 m²
Área base: 20 x 20 x 2 = 800 m²
Volume: 20 x 20 x 30 = 12000 m²

Dez andares com aproximadamente 3 metros de altura cada um, com quarenta
apartamentos por andar, e com cinco pessoas por apartamento.

Considerando um espaçamento de cinco metros entre os apartamentos teríamos:
AB) 25 x 25 = 625 m²
A – total ) 9600 = aproximadamente quinze prédios
625

Quinze prédios:
Dez andares x quarenta apartamentos = quatrocentos apartamentos
Quatrocentos AP x quinze prédios = seis mil apartamentos
Seis mil AP x cinco pessoas por AP = TRINTA MIL PESSOAS
 O projeto de construção dessas moradias na área MNOP ( = 9600 m²) serviriam
como abrigo para trinta mil pessoas ( em torno de 2 m² para cada indivíduo),
diminuindo o agravante problema de distribuição de moradia e exclusão social.
Análise
Em relação a esse exercício, que trás um retângulo com uma área de 200 x 150 =
30000 m², e traçando um projeto habitacional simplificado, conseguimos perceber que
utilizando uma área de nove mil e seiscentos metros quadrados desse total, temos a
possibilidade de abrigar uma quantidade de trinta mil pessoas. Mas esse não é o único
problema que devemos analisar. Podemos também refletir sobre outras perspectivas, como a
arborização, fontes alternativas de energia (para a iluminação pública e residencial, por
exemplo), armazenamento e utilização da água da chuva, assim podemos tornar num ideal em
longo prazo, esse conjunto residencial como „auto-sustentável‟.
Conclusão
Com a necessidade humana por novas formas de estilo de vida e por uma nova
compreensão do espaço em que vivemos, utilizamos a chamada matemática aplicada, para
aplicar os conhecimentos tecnológicos desenvolvidos a serviço da sociedade moderna e das
necessidades que através do tempo foram sendo refletidas, como por exemplo o da habitação,
e principalmente os problemas ambientais, em que seguimos um caminho na procura da
sustentabilidade ambiental, ou até ao dito “desenvolvimento sustentável”, mesmo que debatido
como um termo contraditório. Assim, devemos como criaturas racionais, utilizar de todos os
conhecimentos para garantir o bem da população e do meio que fazemos parte, com toda sua
beleza e exuberância.