Curso Satélite de
Matemática
Sessão n.º 2
Universidade Portucalense
Funções reais de variável real
Definição e generalidades
Uma função é uma correspondência que a qualquer elemento
de um conjunto D faz corresponder um e um só elemento de um
outro conjunto B.
Exemplo 1: A seguinte correspondência é uma função:
f
D
1
7
2,1
-3,3
3,5
2
-4
π
B
Exemplo 2: A seguinte correspondência não é uma função:
f
D
e
3
-3
-1,3(3)
1/7
-5
0
0
B
Esta correspondência não é uma função porque o número 1/7
faz corresponder dois números do conjunto B.
Também não é uma função porque o elemento 0 ∈ D não tem
nenhuma correspondência em B.
O conjunto D (conjunto de partida) chama-se o domínio da
função.
Os elementos do domínio denominam-se os objectos da função.
O conjunto B chama-se o conjunto de chegada da função.
Os elementos do conjunto de chegada que são correspondidos
por um objecto do domínio denominam-se as imagens da
função.
O conjunto das imagens designa-se o contradomínio ou o
conjunto imagem da função.
O contradomínio está contido no conjunto de chegada da
função.
Exemplo: A seguinte correspondência é uma função:
f
e
e
0
0
π
π
D
CD
B
Esta função tem:
• domínio D com objectos 0, π e e;
• Conjunto de chegada B = {0, π, e};
• imagens 0 e e que formam o contradomínio da função.
Uma função diz-se injectiva se a quaisquer dois objectos
diferentes correspondem sempre duas imagens diferentes.
Numa função injectiva, dois objectos diferentes não podem ter a
mesma imagem.
Exemplo 1: A seguinte função é injectiva:
a
D
f
3
b
2
c
1
B
Exemplo 2: A seguinte função não é injectiva:
e
9
-1/2
0
D
f
1,4
2
-4
B
Note-se que a imagem 1,4 é correspondida por dois objectos, o e
e o 0.
Uma função diz-se sobrejectiva se o seu contradomínio for igual
ao conjunto de chegada.
Numa função sobrejectiva não pode existir um elemento do conjunto de chegada que não seja correspondido por um objecto.
Exemplo 1: A seguinte função é sobrejectiva:
10
D
f
3
-20
2
30
1
B
Exemplo 2: A seguinte função não é sobrejectiva:
f
1
2
3
4
D
1
5
0
B
Note-se que 0 ∈ B, mas 0 não é uma imagem. Não existe
nenhum objeto que faz corresponder o 0.
Uma função diz-se bijectiva se ela for simultaneamente injectiva
e sobrejectiva.
Numa função bijectiva, qualquer elemento do conjunto de chegada é correspondido por um, e um só, elemento do domínio.
Exemplo 1: A seguinte função é bijectiva:
101
f
-3
-203
2
300
10
D
B
Exemplo 2: A seguinte função não é bijectiva:
1
2
3
4
D
f
a
b
c
B
Note-se que esta função não é injectiva nem sobrejectiva.
É possível representar qualquer função de uma forma mais
simples, usando a expressão analítica que define a função:
f :D B
x
y  f ( x).
Esta notação lê-se: a função f é uma função de domínio D e
conjunto de chegada B, que a cada objecto x ∈ D faz
corresponder uma e uma só imagem y = f(x) ∈ B.
Neste caso, x diz-se a variável independente e y a variável
dependente da função.
y depende do valor que a variável x assume.
Daqui para a frente interessa-nos estudar funções reais de
variável real.
Uma função diz-se uma função real de variável real se o seu
domínio e o seu contradomínio são dois subconjuntos de ℝ.
Exemplo:

f:
x
y  f ( x)  2 x.
Para o objecto 1, a imagem é y = f(1) = 2 × 1 = 2;
Para o objecto –1, a imagem é y = f(– 1) = 2 × (–1) = –2;
Para o objecto 0.4, a imagem é y = f(0.4) = 2 × 0.4 = 0.8;
Para o objecto π, a imagem é y = f(π) = 2 × π = 2π;
...
...
...
...
...
...
...
Funções polinomiais:
Diz-se que f é uma função polinomial (ou um polinómio) de grau
n ∈ ℕ ∪ {0}, se a sua expressão analítica for dada por

f:
x
y  f ( x)  an x n  an1 x n1  an2 x n2  ...  a2 x 2  a1 x  a0 ,
onde, para qualquer i = 0, …, n, ai ∈ ℝ e an ≠ 0.
Exemplo 1: as funções constantes definidas por

f:
x
y  f ( x)  a0 , a0  ,
são funções polinomiais de grau zero. Qualquer que seja o
objecto do domínio, f faz sempre corresponder a imagem a0.
Gráficos de funções polinomiais de grau 0:
O gráfico de uma função constante é uma recta horizontal que
passa pelo ponto de coordenadas (x = 0, y = a0). Dizemos que a
recta tem ordenada na origem igual a a0.
Estas funções têm domínio ℝ e contradomínio {a0}.
Não são funções injectivas – todos os objectos têm a mesma
imagem.
Exemplo 2: as funções lineares definidas por

f:
x
y  f ( x)  a1 x  a0 , a1 , a0 
são funções polinomiais de grau um.
(a1  0),
Gráficos de funções polinomiais de grau 1:
O gráfico de uma função polinomial de grau 1 é uma recta
oblíqua que tem ordenada na origem igual a a0.
O coeficiente de x, a1, chama-se o declive da recta. O declive está
relacionado com a inclinação da recta (o declive é a tangente da
inclinação).
Estas funções têm domínio ℝ e contradomínio ℝ.
São funções bijectivas.
Exemplo 3: as funções quadráticas definidas por

f:
x
y  f ( x)  a2 x 2  a1 x  a0 , a2 , a1 , a0 
são funções polinomiais de grau dois.
(a2  0),
Gráficos de funções polinomiais de grau 2:
O gráfico de uma função polinomial de grau 2 é uma curva
chamada parábola.
O coeficiente de x2, a2, determina a concavidade da parábola. Se
a2 for negativo, a parábola tem concavidade voltada parta baixo.
Se a2 for positivo, a parábola tem concavidade voltada para cima.
Estas funções têm domínio ℝ mas o seu contradomínio nunca é
ℝ.
Não são funções injectivas porque conseguimos sempre
encontrar dois objectos diferentes que correspondem à mesma
imagem.
Funções racionais:
Diz-se que f é uma função racional se ela for definida como o
quociente entre duas funções polinomiais.
Sejam n(x) e d(x) duas funções polinomiais quaisquer. A função
f :D 
n( x) an x n  ...  a1 x  a0
x
y  f ( x) 

,
m
d ( x) bm x  ...  b1 x  b0
é uma função racional.
Exemplo:
f:
\{0} 
x
1
y  f ( x)  .
x
O gráfico da função anterior é uma curva chamada hipérbole.
Note-se que o número zero não pertence ao domínio da função
anterior, uma vez que 1/0 não tem sentido.
Geralmente, o domínio das funções racionais não é o conjunto
dos números reais.
n( x )
Considere-se uma função racional definida por f ( x) 
.
d ( x)
O domínio de f é o conjunto
D  x 
: d ( x)  0 ,
uma vez que o denominador da função racional não pode ser
zero. Dividir por zero não tem sentido.
Exemplo: determine o domínio da função racional
x2
g ( x)  2 .
x 1
Resolução: o domínio de g é o conjunto formado por todos os x
que fazem com que x2 – 1 não seja igual a zero.
Comecemos por determinar quando é que x2 – 1 é igual a zero:
x2 – 1 = 0 ⇔ (x – 1)(x + 1) = 0 ⇔ x = –1 ∨ x = 1.
Então x não pode ser 1 e x não pode ser –1. O domínio de g é
dado por
Dg = {x ∈ ℝ: x2 – 1 ≠ 0} = {x ∈ ℝ: x ≠ –1 ∧ x ≠ 1}.
O conjunto anterior também pode ser representado por
ℝ\{-1, 1}. Lê-se ℝ excepto -1 e 1.
Gráfico de g:
Funções exponenciais:
Diz-se que f é uma função exponencial de base a se ela for
definida por
f: 
y  f ( x)  a x ,
x
onde a é um número real positivo diferente de 1.
Nota: repare que a variável é x. A base da função exponencial é
uma constante.
Exemplo:

f:
x
y  f ( x )  3x ,
Gráficos de funções exponenciais:
As funções exponenciais têm domínio ℝ e contrdomínio ℝ+.
São funções injectivas porque não existem dois objectos com a
mesma imagem.
Dentro da família das funções exponenciais, a função exponencial de base e (onde e representa o número de Neper) tem uma
grande importância na modelação de uma conta que rende juros
compostos de uma forma contínua.
Se s0 for o capital investido numa conta que é capitalizada
continuamente com a taxa nominal r (de juros compostos), o
valor da conta passados t anos é dado pela função exponencial
f(t) = s0 × ert.
Se se investir 10.000€ com uma taxa de 3% obtém-se o gráfico:
Considerem-se dois depósitos com taxas 3% e 5% e igual s0:
Considerem-se três depósitos com a mesma taxa e diferente s0:
Funções logarítmicas:
Diz-se que f é uma função logarítmica de base a, e define-se

f:
x

y  f ( x)  log a ( x),
quando ay = x, ou seja, y é o número que se tem que elevar a
base a, para se obter x (a > 0 e a ≠ 1).
A função logarítmica de base a diz-se a função inversa da função
exponencial de base a, uma vez que uma anula o efeito da outra:
Função exponencial
ax
x
Função logarítmica
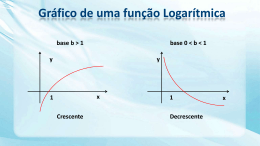
Gráficos de funções logarítmicas:
As funções logarítmicas têm domínio ℝ+ e contrdomínio ℝ.
São funções injectivas porque não existem dois objectos com a
mesma imagem.
Tal como nas funções exponenciais, a função logarítmica de base
e tem uma grande importância. Por isso, representa-se o
logarítmo de base e por f(x) = ln(x), sem se especificar a base. O
logarítmo de base e também é designado por logarítmo natural.
Propriedades dos logarítmos:
1- loga(ax) = x, para qualquer número real x.
2- Como a1 = a, então loga(a) = 1.
3- Como a0 = 1, então loga(1) = 0.
4- a
log a  x 
 x, para qualquer número real positivo x.
5- Sejam x e y dois números reais positivos. Então
loga(x × y) = loga(x) + loga(y).
Demonstração:



log a ( xy )  log a a loga ( x )  a loga ( y )  log a a loga ( x )loga ( y )

 log a ( x)  log a ( y ).
6- Sejam x e y dois números reais positivos. Então
loga(x ÷ y) = loga(x) – loga(y).
7- Seja x um número real positivo e y ∈ ℝ. Então
loga(xy) = y × loga(x).
8- Para fazer cálculos deve-se usar: loga(x) = ln(x) ÷ ln(a).