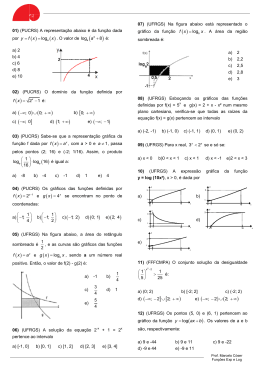
O n ú m e ro "e ": po r qu ê ?
E s t e t ext o foi es cr it o p or E lon La ges Lim a , n o a r t igo “Con ceit os e
con t r ovér s ia s ”, n a Revis t a d o Pr ofes s or d e Ma t em á t ica , 1 9 8 3 , p p .1 0 –1 2 .
As a lt er a ções r ea liza d a s n o t ext o for a m a p en a s à s r efer en t es a m oed a d a
ép oca (1 9 8 3 ) p a r a a m oed a a t u a l (2 0 0 2 ): d e cr u zeir os p a r a r ea is .
A n oçã o d e loga r it m o qu a s e s em p r e n os é a p r es en t a d a , p ela p r im eir a vez, d o
s egu in t e m od o: “0 loga r it m o d e u m n ú m er o y n a b a s e a é o exp oen t e x t a l qu e a x = y”,.
S egu e-s e a ob s er va çã o: “os n ú m er os m a is fr eqü en t em en t e u s a d os com o b a s e d e u m
s is t em a d e loga r it m os s ã o 1 0 , qu e é a b a s e d o n os s o s is t em a d e n u m er a çã o, e o
n ú m er o e = 2 ,7 1 8 2 8 1 8 2 .. .” Is t o n os d eixa in t r iga d os .
De s a íd a , u m a
p er gu n t a
in gên u a : es t a
r egu la r id a d e n a
s eqü ên cia
d os
a lga r is m os d ecim a is d es t e n ú m er o p er s is t e? Nã o. Ap en a s u m a coin cid ên cia n o
com eço. Um va lor m a is p r ecis o s er ia e = 2 ,7 1 8 2 8 1 8 2 8 4 5 9 ...
Nã o s e t r a t a d e u m a fr a çã o d ecim a l p er iód ica . O n ú m er o e é ir r a cion a l, is t o é,
n ã o p od e s er ob t id o com o qu ocien t e e = p / q d e d ois in t eir os . Ma is a in d a : é u m
ir r a cion a l tra n s cen d en te. Is t o s ign ifica qu e n ã o exis t e u m p olin ôm io P(x) com
coeficien t es in t eir os , qu e s e a n u le p a r a x = e.
Por qu e en t ã o a es colh a d e u m n ú m er o t ã o es t r a n h o com o b a s e d e loga r it m os ?
Mes m o d ep ois d e a p r en d er qu e
1

e = lim 1 + 
n
n →∞ 
n
a in d a ga çã o a in d a p er s is t e: o qu e fa z es s e n ú m er o t ã o im p or t a n t e? Is t o é o qu e
p r ocu r a r ei r es p on d er a qu i.
Ta lvez a r es p os t a m a is con cis a s eja qu e o n ú m er o “e” é im p or t a n t e p or qu e é
in evit á vel. S u r ge es p on t a n ea m en t e em vá r ia s qu es t ões b á s ica s .
Um a d a s r a zões p ela s qu a is a Ma t em á t ica é ú t il à s Ciên cia s em ger a l es t á n o
Cá lcu lo (Difer en cia l e In t egr a l), qu e es t u d a a va r ia çã o d a s gr a n d eza s . E u m t ip o d e
va r ia çã o d os m a is s im p les e com u m en t e en con t r a d os é a qu ele em qu e o cr es cim en t o
(ou d ecr es cim en t o) d a gr a n d eza em ca d a in s t a n t e é p r op or cion a l a o va lor d a gr a n d eza
n a qu ele in s t a n t e. E s t e t ip o d e va r ia çã o ocor r e, p or exem p lo, em qu es t ões d e ju r os ,
cr es cim en t o p op u la cion a l (d e p es s oa s ou b a ct ér ia s ), d es in t egr a çã o r a d ioa t iva , et c. E m
t od os os fen ôm en os d es t a n a t u r eza , o n ú m er o e a p a r ece d e m od o n a t u r a l e
in s u b s t it u ível. Veja m os u m exem p lo s im p les .
S u p on h a m os qu e eu em p r es t e a a lgu ém a qu a n t ia d e 1 r ea l a ju r os d e 1 0 0 % a o
a n o. No fin a l d o a n o, es s a p es s oa vir ia p a ga r -m e e t r a r ia 2 r ea is : 1 qu e t om a r a
em p r es t a d o e 1 d os ju r os . Is t o s er ia ju s t o? Nã o. O ju s t o s er ia qu e eu r eceb es s e e
r ea is . Veja m os p or qu e. Há u m en t en d im en t o t á cit o n es s a s t r a n s a ções d e qu e os
ju r os s ã o p r op or cion a is a o ca p it a l em p r es t a d o e a o t em p o d ecor r id o en t r e o
em p r és t im o e o p a ga m en t o. As s im , s e m eu clien t e vies s e m e p a ga r s eis m es es d ep ois
d o em p r és t im o, eu r eceb er ia a p en a s 1
oca s iã o, ele es t a va com 1
1
r ea is . Ma s is t o qu er d izer qu e, n a qu ela
2
1
r ea is m eu s e ficou com es s e d in h eir o m a is s eis m es es , à
2
t a xa d e 1 0 0 % a o a n o, logo d ever ia p a ga r -m e
1
1
1
+
2
2
2
1
1
1

 1
1  = 1 × 1 = 1 +  r ea is
2
2
2

 2
n o fim d o a n o. Is t o m e d a r ia 2 ,2 5 r ea is m a s , m es m o a s s im , eu n ã o a ch a r ia ju s t o. E u
p od er ia d ivid ir o a n o n u m n ú m er o a r b it r á r io n d e p a r t es igu a is . Tr a n s cor r id o o
p r im eir o p er íod o d e
1 ano
1
, m eu ca p it a l em p r es t a d o es t a r ia va len d o 1 +
r ea is . No
n
n
fim d o s egu n d o p er íod o d e
1 ano
 1 ano 
, eu es t a r ia com 

n
 n 
 1 ano 
No fim d o a n o eu d evia r eceb er 

 n 
2
r ea is , e a s s im p or d ia n t e.
n
r ea is . Ma s , com o eu p os s o fa zer es s e
r a ciocín io p a r a t od o n , s egu e-s e qu e o ju s t o e exa t o va lor qu e eu d ever ia r eceb er p elo
m eu cr u zeir o em p r es t a d o s er ia
1

e = lim 1 + 
n
n →∞ 
n
Ma is ger a lm en t e, s e eu em p r es t o c r ea is a ju r os d e k % a o a n o, t r a n s cor r id os t
a n os eu d evo r eceb er d e volt a c.e αt r ea is , on d e α =
k
. Pa r a m a ior es d et a lh es e
100
ou t r os exem p los , r ela t ivos a d es in t egr a çã o r a d ioa t iva , cr es cim en t o p op u la cion a l, et c.,
veja o livr in h o “Loga r it m os ”1 , d e m in h a a u t or ia , p u b lica d o p ela S .B.M.
1
Elon Lages Lima, Logarítmos. Coleção do PROFESSOR DE MATEMÁTICA, Sociedade Brasileira de Matemática
Os loga r it m os qu e t êm b a s e e s ã o à s .vezes im p r op r ia m en t e ch a m a d os d e
“loga r it m os n ep er ia n os ”. Na r ea lid a d e, os loga r it m os or igin a lm en t e in t r od u zid os p or
Na p ier t in h a m p or b a s e o n ú m er o a = (1 -1 0 -7 )7 . Aliá s , p a r a s er m os m a is exa t os , o
ver d a d eir o “loga r it m o n ep er ia n o” d o n ú m er o x er a igu a l a
 x 
 .
1 0 7 . log a 
 10 7 
É m a is a p r op r ia d o ch a m a r loga ritm os n a tu ra is a os loga r it m os d e b a s e e. E u ler os
ch a m a va d e loga ritm os h iperb ólicos , p elo s egu in t e m ot ivo. Con s id er em os a fu n çã o
f: R + → R, d efin id a p or f(x) =
1
. S eu gr á fico é u m r a m o d e h ip ér b ole equ ilá t er a . Pa r a
x
ca d a n ú m er o r ea l a > O, s eja H 1a fa ixa d e h ip ér b ole for m a d a p elos p on t os d o p la n o
cu ja s coor d en a d a s (x, y) s a t is fa zem à s d es igu a ld a d es 0 ≤ y ≤
1
e 1 ≤ x ≤ a (s e a ≥ 1 ) ou
x
a ≤ x ≤ 1 (s e a ≤ 1 ).
A á r ea d e H 1a é igu a l a o loga r it m o n a t u r a l d e a s e for a ≥ 1 e a es s e loga r it m o com
s in a l t r oca d o s e for a ≤ 1 . E m p a r t icu la r , o. n ú m er o e é a a b s cis s a t a l qu e H1e t em
á r ea igu a l a 1 . O fa t o d e qu e a á r ea d a fa ixa d e h ip ér b ole H 1a é igu a l a o loga r it m o
n a t u r a l d e a p od e s er t or n a d o com o d efin içã o d e loga r it m o e p er m it e d es en volver a
t eor ia , a p a r t ir d a í, d e m od o s im p les e elega n t e. E s t a a b or d a gem é a d ot a d a em n os s o
livr o a cim a cit a d o.
“0 loga r it m o h ip er b ólico p od e s er ca r a ct er iza d o p ela igu a ld a d e log (1 + x) = x,
p a r a t od o n ú m er o in fin it a m en t e p equ en o x.” E s t a fr a s e é d e E u ler . E vid en t em en t e,
n a t eor ia h a b it u a l d os n ú m er os r ea is , n ã o h á n ú m er os in fin it a m en t e p equ en os . O
qu e E u ler qu is d izer é qu e log (1 + x) e x s ã o “in fin it és im os equ iva len t es ” ou , d e m od o
m a is p r ecis o, qu e
log(1 + x )
= 1.
x
x →0
lim
E s t a igu a ld a d e s ó é ver d a d eir a qu a n d o a b a s e d o s is t em a d e loga r it m os é o n ú m er o e.
S e t om a r m os loga r it m os n u m a b a s e a t er em os
log(1 + x )
=c,
x
x →0
lim
on d e c é o loga r it m o n a t u r a l d e a . Na ver d a d e, es t a fór m u la é u m ca s o p a r t icu la r d o
fa t o d e qu e a d er iva d a d a fu n çã o log x é igu a l a
c
. Aqu i t om a m os log x n u m a b a s e a
x
qu a lqu er . S e a b a s e for e en t ã o a d er iva d a d e log x s er á
c = log e a .) Ma is u m a vez, vem os qu e a b a s e e é m a is “n a t u r a l”.
1
. (No ca s o ger a l,
x