Nome: _________________________________________
____________________________ N.º: __________
endereço: ______________________________________________________________ data: __________
Telefone:_________________ E-mail: _________________________________________________________
PARA QUEM CURSA A 2 a. SÉRIE DO ENSINO MÉDIO EM 2014
Colégio
Disciplina:
Prova:
MaTeMÁTiCa
desafio
nota:
QUESTÃO 16
3
228 + 230
–––––––––– =
10
28
29
a) –––
5
b) –––
5
c) 28
d) 29
e)
1
––
3
冢 –––
10 冣
258
RESOLUÇÃO
3
228 + 230
–––––––––– =
10
3
1 . 228 + 22 . 228
–––––––––––––––
10
=
3
5 . 228
––––––– =
10
3
3
228
227 =
–––– = 兹苶苶
2
3
(29)3
兹苶苶
= 29
Resposta: D
QUESTÃO 17
A diferença entre o cubo da soma de dois números inteiros e a soma de seus cubos pode ser:
a) 4
b) 5
c) 6
d) 7
e) 8
RESOLUÇÃO
Sendo a Œ e b Œ , temos a . b Œ e a + b Œ , assim:
(a + b)3 – (a3 + b3) = a3 + 3a2b + 3ab2 + b3 – a3 – b3 = 3a2b + 3ab2 = 3 . ab . (a + b) é múltiplo
de 3, podendo ser igual a 6.
Resposta: C
OBJETIVO
1
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 18
Cada um dos cartões abaixo tem de um lado um número e do outro uma letra.
Alguém afirmou que todos os cartões que têm uma vogal numa face têm um número par na
outra.
Para verificar se tal afirmação é verdadeira:
a) é necessário virar todos os cartões.
b) é suficiente virar os dois primeiros cartões.
c) é suficiente virar os dois últimos cartões.
d) é suficiente virar os dois cartões do meio.
e) é suficiente virar o primeiro e o último cartão.
RESOLUÇÃO
Para confirmar a afirmação “todos os cartões que têm uma vogal numa face têm um
número par na outra”, basta virar o primeiro (pois como A é vogal deve aparecer um
número par na outra face), e o último (para confirmar que não há vogal na outra face
do 3 que é ímpar). Observe que, no caso de haver uma consoante, pode aparecer
qualquer número na outra face, já que a afirmação não cita este fato.
Reposta: E
QUESTÃO 19
Uma caixa contém 100 bolas apenas. Destas, 30 são brancas, 30 são verdes, 30 são azuis e,
entre as 10 restantes, algumas são pretas e outras vermelhas. O menor número de bolas que
devemos tirar da caixa, sem lhes ver a cor, para termos certeza de que, pelo menos, 10 delas
são da mesma cor, é:
a) 11
b) 21
c) 33
d) 38
e) 48
RESOLUÇÃO
Retirando-se 9 bolas brancas, 9 verdes, 9 azuis e as 10 restantes entre pretas e
vermelhas, num total de 37 bolas, ainda não temos a garantia de 10 serem da mesma
cor, o que ocorrerá a partir da retirada da 38a. bola.
Resposta: D
OBJETIVO
2
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 20
Um casal tem filhos e filhas. Cada filho tem o número de irmãos igual ao número de irmãs.
Cada filha tem o número de irmãos igual ao dobro do número de irmãs. Qual é o total de filhos
e filhas do casal?
a) 3
b) 4
c) 5
d) 6
e) 7
RESOLUÇÃO
Sendo m e h, respectivamente, o número de filhas e de filhos do casal, temos:
冦
m=h–1

h = 2 . (m – 1)

冦m = 3
h=4
冦
m–h=–1
h = 2m – 2

冦
h–m=1

– h + 2m = 2
冦
h–m=1

m=3
ﬁh+m=4+3=7
Resposta: E
QUESTÃO 21
Na equação ax2 + bx + c = 0, com a. b . c ⫽ 0 e 3b2 = 16ac, tem-se:
a) as raízes são reais e iguais
b) as raízes não têm mesmo sinal
c) uma raiz é o triplo da outra
d) V = Ø
e) V = {1; – 1}
RESOLUÇÃO
3b2
Na equação ax2 + bx + c = 0, tem-se 3b2 = 16ac  –––– = 4ac, então:
4
I) ∆ =
b2
– 4ac =
b2
3b2
b2
4b2 – 3b2
=
=
–––––
––––––––––
––––
–
4
4
4
b
– 2b ± b
– b ± –––
––––––––
∆
– 2b ± b
– b ± 兹苵苵
2
2
II) x = ––––––––– = –––––––––– = ––––––––––– = –––––––– 
4a
2a
2a
2a
–b
– 3b
 x1 = ––––– ou x2 = ––––– ﬁ x2 = 3 . x1
4a
4a
Resposta: C
OBJETIVO
3
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 22
Para dar R$ 1,80 de troco a um cliente, o caixa de um supermercado pretende usar
exatamente 20 moedas. Se ele dispõe apenas de moedas de 5 centavos, 10 centavos e 25
centavos, de quantos modos distintos ele pode compor tal quantia?
a) 3
b) 4
c) 5
d) 6
e) 7
RESOLUÇÃO
Sendo x, y e z as quantidades de moedas de R$ 0,05, R$ 0,10 e R$ 0,25,
respectivamente, tem-se 0,05x + 0,10y + 0,25z = 1,80, com x, y e z Œ .
Assim,
冦 x + y + z = 20
x + 2y + 5z = 36
冦 y + 4z = 16
x + y + z = 20
ﬁ
ﬁ
冦 y = 16 – 4z
x = 4 + 3z
Como y Œ , devemos ter 16 – 4z ≥ 0  z ≤ 4.
Desta forma, as soluções do sistema são (4; 16; 0), (7; 12; 1), (10; 8; 2), (13; 4; 3) e (16;
0; 4).
Portanto, existem 5 modos distintos de compor R$ 1,80 com moedas de R$ 0,05, R$
0,10 e R$ 0,25, usando exatamente 20 moedas.
Resposta: C
QUESTÃO 23
Num grupo de estudantes, 80% estudam inglês, 40% estudam francês e 10% não estudam
nenhuma destas duas línguas. Nesse grupo, a porcentagem de alunos que estudam ambas
as línguas é:
a) 25%
b) 50%
c) 15%
d) 33%
e) 30%
RESOLUÇÃO
I) Representando num diagrama, tem-se:
I
F
80% - x
x
40% - x
10%
II) 80% – x + x + 40% – x + 10% = 100%  x = 30%
Resposta:MAT-0012137-a1pb
E
OBJETIVO
4
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 24
Numa função f tal que f(x + 2) = 3f(x) para todo x real, sabe-se que f(2) + f(4) = 60. Então f(0)
vale:
a) 2
b) 4
c) 5
d) 6
e) 8
RESOLUÇÃO
Se f(x + 2) = 3 . f(x) e f(2) + f(4) = 60, tem-se:
I) Para x = 2 ﬁ f(2 + 2) = 3 . f(2)  f(4) = 3 . f(2)
II) f(2) + f(4) = 60 ﬁ f(2) + 3 . f(2) = 60  4 . f(2) = 60  f(2) = 15
III) Para x = 0 ﬁ f(0 + 2) = 3 . f(0)  f(2) = 3 . f(0)  15 = 3 . f(0)  f(0) = 5
Resposta: C
QUESTÃO 25
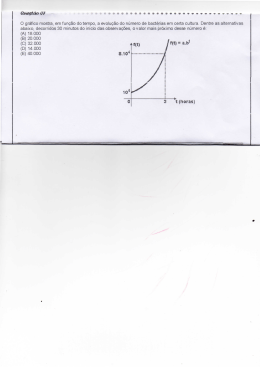
Sabe-se que o número de bactérias num meio, sob certas condições, duplica a cada 10 minutos.
No instante inicial, o número de bactérias era 5000. Qual a expressão que descreve corretamente como varia o número de bactérias, N, em função do tempo, t, em minutos?
t
––––
10
2t
a) N = 5000 . ––––
10
b) N = 5000 . 2
2t
c) N = 5000 + ––––
10
2t
d) N = 5000 + ––––
10
2t
e) N = 5000 . ––––
10
RESOLUÇÃO
Se o número de bactérias dobra a cada 10 minutos, tem-se:
I) Número inicial de bactérias: 5000
II) Após 10 . 1 minutos: 5000 . 21
III) Após 10 . 2 minutos: 5000 . 22
t
⯗
–––
10
Assim, após t minutos, o número de bactérias é dado por N = 5000 . 2
Resposta: B
OBJETIVO
5
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 26
Considere a função invertível f :  definida por f(x) = 2x + b, em que b é uma constante.
Sendo f – 1 a sua inversa, qual o valor de b, sabendo-se que o gráfico de f – 1 passa pelo ponto
A (1, – 2)?
a) – 2
b) – 1
c) 2
d) 3
e) 5
RESOLUÇÃO
I) (m, n) Œ f – 1  (n; m) Œ f, assim, se A(1; – 2) Œ f – 1, então, A’(– 2; 1) Œ f
II) A’(– 2; 1) Œ f  f(– 2) = 1, assim, para f(x) = 2x + b tem-se,
2 . (– 2) + b = 1  – 4 + b = 1  b = 5
Resposta: E
QUESTÃO 27
x–3
O número de soluções inteiras da inequação ——– ≥ 2 é:
x–1
a) 0
b) 1
c) 2
d) 3
e) 4
RESOLUÇÃO
x–3
x – 3 – 2 ⭓ 0  (x – 3) – 2(x – 1) ⭓ 0  x – 3 – 2x + 2 ⭓ 0 
–––––––
⭓ 2  –––––––
–––––––––––––––
–––––––––––––
x–1
x–1
(x – 1)
x–1
–x–1
 –––––––– ⭓ 0  (– x – 1).(x – 1) ⭓ 0 e x ⫽ 1
x–1
As raízes são – 1 e 1 e o gráfico é do tipo
-1
-
+
1
-
x
Logo, – 1 ⭐ x ⬍ 1
As soluções inteiras são – 1 e 0.
MAT-0012026-apb
Resposta: C
OBJETIVO
6
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 28
Em um terreno de formato triangular, deseja-se construir uma casa com formato retangular.
Determine x e y de modo que a área construída seja máxima
a) x = 2,5 e y = 7,5
b) x = 3 e y = 9
c) x = 4,5 e y = 10,5
d) x = 5 e y = 15
e) x = 3 e y = 10
RESOLUÇÃO
I) Por semelhança de triângulos, podemos afirmar que
15 – y
x
––– = –––––––  3x = 15 – y  y = 15 – 3x
15
5
II) A área do retângulo é dada por A = x . y = x . (15 – 3x) = – 3x2+ 15x
III) A área é uma função do 2o. grau cujo gráfico é uma parábola com concavidade para
baixo (a < 0).
Portanto, a área máxima ocorre para
– 15
b
xv = – ––– = –––––– = 2,5
–6
2a
IV) Para x = 2,5, temos: y = 15 – 3 . (2,5) = 15 – 7,5 = 7,5
Resposta: A
QUESTÃO 29
Ao preço de R$ 30,00 por caixa, uma fábrica de sorvete vende 400 caixas por semana. Cada
vez que essa fábrica reduz o preço da caixa em R$ 1,00, a venda semanal aumenta em 20 caixas. Se a fábrica vender cada caixa por R$ 25,00, sua receita semanal será de
a) R$ 14.000,00
b) R$ 13.200,00
c) R$ 12.500,00
d) R$ 11.600,00
e) R$ 11.100,00
RESOLUÇÃO
I) Seja x o preço unitário da caixa e y a quantidade de caixas vendidas por semana.
receita = x . y ﬁ receita = 30 . 400 = 12 000 reais
II) Como a cada 1 real de redução no preço há um aumento de 20 caixas, então na
redução de 5 reais no preço teremos um aumento de 100 caixas.
III) Se o preço da caixa for 25 reais, a quantidade de caixas vendidas será de 500 unidades. Logo, a nova receita passará a ser 25 . 500 = 12 500 reais.
Resposta: C
OBJETIVO
7
MATEMÁTICA – DESAFIO – 2.a SÉRIE
QUESTÃO 30
Uma função real f do 1o. grau é tal que f(0) = 1 + f(1) e f(–1) = 2 – f(0). Então f(3) é igual a:
a) – 3
5
b) – —2
c) – 1
d) 0
7
e) —2
RESOLUÇÃO
f(x) é do 1o. grau, logo f(x) = ax + b.
I) f(0) = 1 + f(1) ﬁ a . 0 + b = 1 + a . 1 + b  a = – 1
II) f(– 1) = 2 – f(0) ﬁ a . (– 1) + b = 2 – (a . 0 + b) 
1
 – a + b = 2 – b  2b = 2 + a ﬁ 2b = 2 + (– 1)  b = –––
2
De I e II, temos:
1
f(x) = – x + –––
2
5
1
Então, f(3) = – 3 + ––– = – –––
2
2
Resposta: B
OBJETIVO
8
MATEMÁTICA – DESAFIO – 2.a SÉRIE