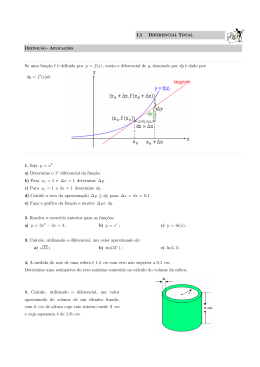
ACRÉSCIMOS E DIFERENCIAIS
Definição: Seja f (x) uma função real de variável real diferenciável em x,
f : x → y = f ( x)
Se ∆x é um acréscimo de x então
a) chama-se diferencial de x e representa-se por dx ao número real
dx = ∆ x
b) chama-se diferencial de f em x e representa-se por dy ao número real
dy = f ′( x)∆ x
NOTA 1: Se ∆x ≈ 0 então ∆y ≈ dy e assim dy pode ser utilizado como
aproximação à variação exacta ∆y da variável dependente.
Exemplo: Considere a seguinte função f ( x) = x 4 − 3 x 2 + 5 x + 4 . Calcule um
valor aproximado para f (1.9) .
Definição: Se f (x) é uma função diferenciável no conjunto A ⊂ D f , então
para um dado acréscimo ∆x podemos considerar a função
df : A → IR
x → dy = f ′( x)dx
Se esta função for diferenciável em x, então podemos considerar a quantidade
d 2 y = d (dy ) que se denomina por segunda diferencial de f em x, dada por
d 2 y = f ′′( x)dx 2