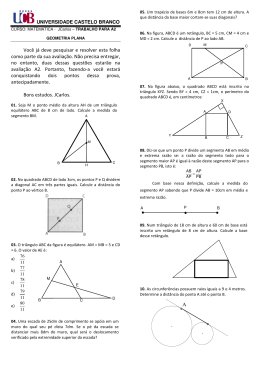
LISTA DE EXERCÍCIOS DE GEOMETRIA PLANA
01) FUVEST - A medida do ângulo ADC inscrito na circunferência de centro O é:
a) 125o
b) 110o
c) 120o
d) 100o
e) 135o
D
A
C
35
B
O
02) Num triângulo ABC de lados AB = 12 , AC = 8 e BC = 10 , a medida do maior segmento que a bissetriz interna
do ângulo  , determina sobre BC é:
a) 4,0
b) 5,5
c) 6,0
d) 6,5
e) 7,0
03) FUVEST - Os lados de um triângulo medem
a)
1
b)
2
c)
3
d)
5
e)
15
5 , 10 e 5 . Qual o comprimento da altura relativa ao lado maior?
04) A área da coroa circular limitada pelas circunferências inscritas e circunscritas a um triângulo eqüilátero de lado 2 , é:
a)  - 1
b) /2
c) 2
d) 
e)  + 1
05) FUVEST - No quadrilátero abaixo, BC = CD = 3 cm , AB = 2 cm , ADC = 60 o E ABC = 90o . A medida, em cm,
do perímetro do quadrilátero é:
D
C
a) 11
b) 12
c) 13
d) 14
e) 15
A
B
06) FUVEST - Na figura abaixo, AD = 2 cm , AB =
ponto do lado AC. A medida do lado BC , em cm, é:
B
a) 3
b) 2
c)
5
d)
6
e)
7
3 cm , a medida do ângulo BÂC é 30o e BD = DC onde D é
A
D
C
07) FUVEST - Considere o triângulo representado na malha pontilhada com quadrados de lados iguais a 1 cm. A área do
triângulo , em cm2, é:
    
a) 2
    
b) 3
    
c) 4
    
d) 5
    
e) 6
08) FUVEST - Os pontos A , B e C são vértices consecutivos de um hexágono regular de área igual a 6. Qual a área do
triângulo ABC ?
A
B
a) 1
b) 2
c) 3
C
d)
2
e)
3
09) FUVEST - No quadrilátero ABCD abaixo, ABC = 150 o , AD = AB = 4 cm , BC = 10 cm , MN = 2 cm , sendo
M e N , respectivamente, os pontos médios de CD e BC . A medida, em cm 2 , da área do triângulo BCD é:
D
a) 10
b) 15
c) 20
d) 30
e) 40
M
C
A
N
B
10) FUVEST - No triângulo ABC , AB = 20 cm , BC = 5 cm e o ângulo ABC é obtuso. O quadrilátero MBNP é um
losango de área 8 cm2 . A medida, em graus, do ângulo BNP é:
A
a) 15
b) 30
c) 45
d) 60
e) 75
M
P
B
N
C
11) FUVEST - No triângulo ABC , AC = 5 cm , BC = 20 cm e cos  = 3/5 . O maior valor possível, em cm2, para a
área do retângulo MNPQ , construído conforme mostra a figura. é:
A
a) 16
b) 18
c) 20
d) 22
e) 24
M
N

B
N
P
C
12) FUVEST - O retângulo ABCD representa um terreno retangular cuja largura é 3/5 do comprimento. A parte hachurada
representa um jardim retangular cuja largura é também 3/5 do comprimento. Qual a razão entre a área do jardim e a área total
do terreno ?
A
B
a) 30 %
b) 36 %
c) 40 %
d) 45 %
e) 50 %
D
C
13) FUVEST - No papel quadriculado da figura abaixo, adota-se como unidade de comprimento o lado do quadrado
hachurado. DE é paralelo a BC.
C
E
A
D
B
Para que a área do triângulo ADE seja a metade da área do triângulo ABC , a medida de AD , na unidade adotada é:
a) 4 2
b) 4
c) 3 3
8 3
3
7 3
e)
2
d)
14) FUVEST - As retas r e s são paralelas. A medida do ângulo x , em graus, é:
a) 30
b) 40
c) 50
d) 60
e) 70
x
r
s
120o
140o
15) FUVEST - No retângulo abaixo, o valor, em graus, de  +  é:
a) 50
b) 90
c) 120
d) 130
e) 220
40o


16) FUVEST - No triângulo acutângulo ABC a base AB mede 4 cm e a altura relativa a essa base também mede 4 cm.
MNPQ é um retângulo cujos vértices M e N pertencem ao lado AB , P pertence ao lado BC e Q ao lado AC. O
perímetro desse retângulo, em cm é :
C
a) 4
b) 8
c) 12
d) 14
e) 16
Q
A
P
M
N
B
17) FUVEST - A figura representa um retângulo ABCD e um losango AECF com E no lado BC e F no lado AD.
A
F
D
Se AB = 15 cm e BC = 25 cm , então a medida, em cm,
de um lado do losango é:
B
E
C
a) 13
b) 14
c) 15
d) 16
e) 17
18) VUNESP - A área de um triângulo retângulo isósceles cujo perímetro é 2 vale:
a) 2  2
b) 2  2
c) 3  2
d) 3  2 2
e) 1  2
19) FUVEST - Numa circunferência de raio 1 está inscrito um quadrado. A área da região interna à circunferência e externa
ao quadrado é:
a) maior que 2
b) igual a área do quadrado
c) igual a 2 - 2
d) igual a  - 2
e) igual a /4
20) FUVEST - Um comício político lotou uma praça semicircular de 130 m de raio. Admitindo-se uma ocupação média de
4 pessoas por m2 , qual é a melhor estimativa do número de pessoas presentes ?
a) dez mil
b) cem mil
c) meio milhão
d) um milhão
e) muito mais que um milhão
21) FUVEST - Aumentando-se os lados a e b de um retângulo de 15 % e 20 % respectivamente, a área do retângulo é
aumentada de:
a) 35 %
b) 30 %
b) 3,5 %
d) 3,8 %
e) 38 %
22) UFMG - Observe a figura.
a) 1,5
b) 1
c) 2
d) 0,5
Nessa figura, está representado um canteiro retangular de 6 m de
largura por 10 m de comprimento, cercado por um passeio de
largura constante. Se a área do passeio é de 36 m2 , a medida de
sua largura, em metros, é:
23) UFMG - Observe a figura abaixo, ABCD é um quadrado de lado 1 , EF = FC = FB e ED = 1/2. A área do triângulo
BCF é:
a) 5/16
b) 1/5
c) 1/6
d) 3/4
D
C
E
F
A
B
24) UFMG - Observe a figura abaixo, onde os segmentos AD e BC são paralelos, AD = 8 , AB = 3 e BC = 7. Sendo
P o ponto de interseção das retas AB e DC , a medida do segmento BP é:
D
C
a) 23
b) 22
c) 24
d) 21
A
B
25) UFMG - Observe a figura abaixo. Nessa figura, o trapézio ABCD tem altura 2 3 e bases AB = 4 e DC = 1 . A
medida do lado BC é:
D
C
a) 14
b) 14
c) 4
d)
13
60
A
B
26) Na figura, os triângulos ABD e ACD estão inscritos na circunferência de raio
e BAC = 29o , então o lado CD , em cm mede:
a) 1
A
b) 2
c) 3/2
d) 3
e) 2
2 cm. Se ABD = 85o , ADB = 21o
X
29
21
B
85
D
29
85
C
27) ABCD é um quadrado. Três retas paralelas, a , b e c passam pelos vértices A, B e C , respectivamente. A distância
entre a e b é 5 cm, e a distância entre b e c é 7 cm. A área desse quadrado, em cm2 , é:
a
a) 64
b) 74
c) 78
d) 81
e) 100
A
b
D
B
C
c
28) Na figura mostra uma placa retangular de cartolina com comprimento igual ao dobro da largura. Corta-se em cada canto
um quadrado de lado 2 cm. Em seguida, as abas são dobradas para cima, ao longo das linhas pontilhadas, formando uma
caixa retangular sem tampa, de volume 140 cm3. A área da cartolina usada, em cm2 , é:
2
a) 158
b) 160
c) 162
d) 164
e) 242
2
2
2
2
2
2
2
29) Na figura, AB é paralelo a CD, ACB = 90 o , AC = BC e AB = BD. Sendo CBD = x , o valor de x , em graus é:
D
a) 10
b) 12
c) 15
d) 18
e) 20
C
X
A
B
30) Arquimedes (287 a.C.) tri-seccionava um ângulo arbitrário DÔC =  usando a figura abaixo. Prove que o ângulo
DÂE = /3 . Dado: BA = OE = R
D
B
C
R
A
c: circunferência de raio R.

O
R
E
31) VUNESP - O segmento AB da figura passa pelo centro do círculo e mede 12 cm. O ângulo BÂC é de 15 o . A área da
C
região sombreada é igual a:
B
a) 1,5.
b) 3.
c) 2.(4 + )
d) 6.(3 + 2.)
e) 3.(3 + )
A
32) VUNESP - A circunferência de centro C da figura tem 8 cm de raio. Se AP = 2 cm , então a medida de AM é:
a) 2 3 cm
M
b) 6 3 cm
c) 8 3 cm
A
P
C
d) 4 2 cm
e) 4 cm
33) Na figura, AC = AB = BD . Pode-se afirmar que, necessariamente,
a) y
b) y
c) y
d) y
e) y
=
=
=
=
=
3x
x + 60o
180o - x
2x
1,5.x
B
Y
X
C
A
D
DESAFIOS
34) VUNESP - No quadrilátero ABCD , representado na figura, os ângulos internos A e C são retos, os ângulos CDB e
ADB medem, respectivamente, 45o e 30o e o lado CD 2 cm. Os lados AD e AB medem respectivamente, em cm:
A
a)
5 e
3
b)
5 e
2
c)
6 e
5
d)
6 e
3
e)
6 e
2
B
D
C
35) VUNESP - Na figura abaixo, consideremos os quadrados de lados x , 6 cm e 9 cm. A área do quadrado de lado x em
cm2 é:
a) 9
b) 12
c) 15
d) 16
e) 18
9 cm
6 cm
X
36) VUNESP - Constrói-se um canteiro retangular aproveitando a parte de uma parede já existente e 24 m de tela de arame.
Nas condições dadas, a área desse canteiro é a maior possível. O valor dessa área em m2 é:
a)576
b) 280
c) 144
d) 72
e) 64
tela
37) UELON - Na figura abaixo, o triângulo ABC é eqüilátero, o triângulo ABD é retângulo em A e BC = CD. Nessas
condições , se S , S1 e S2 são respectivamente, as áreas dos triângulos ABD , ABC e ACD , então :
1
a) S  S
2
3
2
b) S  S
1
3
1
c) S 2  S
2
3
d) S  S
1
4
4
e) S 2  S
5
A
B
C
D
38) A circunferência de raio a é tangente as duas semi-circunferências menores e a semi-circunferência maior. Então se
MN = NP = r , o valor de a é:
a) r/2
b) r/3
c) r/4
d) r/5
e) r/6
M
N
P
39) No interior de um triângulo tomamos três circunferências de mesmo raio e tangentes entre si e aos lados do triângulo,
como mostra a figura. Sendo o triângulo retângulo de catetos iguais a 3 e 4 cm, então o raio dessas circunferências em cm é:
a) 1/2
b) 3/4
c) 2/5
d) 3/2
e) 2/3
40) No retângulo ABCD os segmentos PB , BQ , DR e SD tem a mesma medida. Sendo que AB = 13 cm e BC = 7
cm , então, o valor da área máxima da figura sombreada em cm2 será:
A
a) 25
b) 30
c) 40
d) 50
e) 60
p
B
Q
S
D
R
C
41) Na figura abaixo o quadrado hachurado está inscrito em outro de lado igual a 6 cm. Então a área mínima do quadrado
inscrito em cm2 é:
a) 16
b) 18
c) 20
d) 14
e) 12
42) O pentágono ABCDE abaixo está inscrito em uma circunferência de centro O. O ângulo central CÔD mede 60o . Então
o valor de x + y é:
E
x
a) 180o
b) 190o
A
c) 200o
D
d) 210o
O 60
e) 220o
B y
C
43) ABCD é um quadrado de área igual a 1. São tomados dois pontos P  AB e Q  AD tais que PA + AQ = AD. A área
máxima do triângulo APQ é:
D
a) 1/4
b) 1/6
c) 1/8
d) 1/5
e) 1/7
C
Q
A
GABARITO:
01) a 02) c
15) d 16) b
29) c
31) e
03) a
17) e
32) d
04) d
18) d
33) a
05) b
19) d
34) e
06) a
20) b
35) d
07) a
21) e
36) d
08) a
22) b
37) c
P
09) c
23) a
38) a
B
10) b
24) d
39) a
11) c
25) d
40) d
12) b
26) e
41) b
13) a
27) b
42) d
14) e
28) c
43) c