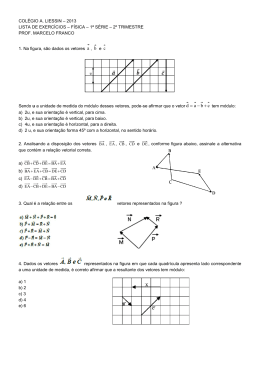
Universidade Estadual de Mato Grosso do Sul
Escola Estadual Presidente Tancredo Neves
Projeto de Extensão: Avaliando o Ensino e a Aprendizagem de Física à
Distância no Ensino Médio: Abordando a Dinâmica
Acadêmica: Ana Paula Langaro, 2ºano do curso de Física.
Orientador: Nilson Oliveira da Silva, Técnico do Laboratório de Física do Curso de Física da
UEMS.
Módulo I - Conceitos de Vetores e Força.
O módulo I tem o objetivo de familiarizar você aluno do ensino médio com vetores, já
falando de um assunto muito importante na Dinâmica que é a Força.
Veja o link a seguir, sobre grandezas vetoriais:
http://efisica.if.usp.br/mecanica/universitario/vetores/intro/
Todos nós estamos acostumados a trabalhar com valores numéricos absolutos que são o
módulo das medidas, o vetor representa medidas que tem além do módulo, direção e sentido. Ele é

representado por uma seta sobre a variável que representa dessa forma: v .

Considere um vetor v de módulo 2u direção horizontal e sentido positivo, ele pode ser
representado da seguinte forma: Veja mais no link:
http://efisica.if.usp.br/mecanica/universitario/vetores/vetores/
Podemos somar dois vetores, veja como:
A
B
Na brincadeira do cabo de guerra um grupo de pessoas se divide em dois grupos iguais, cada
grupo segura a corda em uma de suas extremidades, ninguém pode puxar a corda até que outra
pessoa de um sinal. Quando o sinal é dado todos começam a puxar o grupo A puxa a cora da para a
esquerda e o grupo B puxa a corda para a direita. Enquanto os grupos puxam a corda cada um para
um lado, eles estão aplicando uma força. A direção que os grupos puxam a corda é horizontal, mas
o sentido deve ser escolhido por nós. Vamos supor que o sentido positivo seja da esquerda para a
direita. O grupo A puxa a corda com uma força

F
A

F
e o grupo B puxa a corda com uma força B ,
veja a representação:
A

F
A

F
B
B
Com estas informações podemos saber qual grupo irá vencer a brincadeira, o módulo das
forças é

F
A =5u;

F
e B =5u. Sabendo da direção e do sentido, vamos somar os vetores, a soma do
modulo das forças é chamada de Força resultante. Mas lembre-se que a

F
A
está no sentido negativo,
logo seu módulo será negativo.
Veja:
F = 5− 5
R
F = 0u
R
Quando a Força resultante é zero, significa que a corda não se move, dessa forma ninguém
irá vencer a brincadeira.
Agora vamos supor que no grupo B entra mais um integrante e o módulo de
F
F
R
= 7− 5
R
= 2u

F
A =5u;

F
e B =7u.
Como a Força resultante é 2u o sentido é positivo, na direção horizontal, o grupo B
conseguirá vencer o grupo A.
Veja mais no link: http://efisica.if.usp.br/mecanica/universitario/vetores/oper_vetores/
Agora tente fazer:
Se a

F
A =8u;

F
e B =7u, mostre que grupo irá ganhar:
Veja um vídeo relacionado ao assunto no link a seguir:
http://www.youtube.com/watch?
v=dh_pxkBTekY&feature=PlayList&p=926C7A2858E0FF60&index=5
As crianças que estavam brincando de cabo de guerra, agora resolveram puxar uma caixa
que está cheia de presentes. Cada grupo prendeu uma corda na caixa e a esticou. Começaram a
puxar a caixa cada um para um lado e viram que a caixa se movimenta. Como nós podemos
descobrir para que direção esta caixa irá se movimentar? Qual a intensidade da força com que a
caixa está sendo puxada, e o sentido? O vetor C representa a Força que o grupo C está exercendo
para puxar a caixa, e o vetor D representa a força com que o grupo D está puxando a caixa.
No caso do cabo de guerra a força resultante era a soma das forças, mas neste caso como
existe um ângulo entre as forças teremos que usar a regra do paralelogramo que é a seguinte:
Regra do Paralelogramo:


Uma outra maneira de obter a força resultante entre os vetores C e D , está mostrada na


figura 1. Estes vetores são traçados de modo que suas origens coincidam, como neste caso C e D
,estão representando duas forças aplicadas no ponto 0 (origem). Traçando um paralelogramo que


tenha C e D , como lados a força resultante será dada pela diagonal deste paralelogramo que
parte da origem comum dos dois vetores. A Regra do Paralelogramo nos permite visualizar apenas
a direção e o sentido da força resultante. Veja:

C

D

FR
Figura 1: Representação da
Regra do Paralelogramo
A regra do paralelogramo nos mostra que o sentido da força e a direção, a direção é
apontada pela seta vermelha, isto é, a caixa irá se mover na direção da seta. E o sentido é positivo.


Supondo que o ângulo seja de 60°, e o módulo da Força C seja 5u e o módulo de D seja
8u. Como podemos fazer para encontrar o módulo da Força resultante?
Para isto vamos usar a Lei do Cossenos que estabelece uma relação entre um lado do
triângulo, seu ângulo oposto e os lados que definem este ângulo através da trigonometria.
Veja a equação que devemos usar:
c 2 = a 2 + b 2 − 2ab. cos 60°
Agora vamos calcular o módulo da força resultante:
2
FR = 5 2 + 8 2 − 2 * 8. cos 60
se cos60°=0,5, temos que:
FR =
5 2 + 8 2 − 2 * 8 * 0,5 =
81 = 9u
Assim temos que o módulo da Força resultante é 9u.

Agora tente fazer, supondo que o ângulo seja de 30°, e o módulo da Força C seja 5u e o

módulo de D seja 8u. Como podemos fazer para encontrar o módulo da Força resultante? (dado:
cós 30°=0,86)
Veja mais em: http://efisica.if.usp.br/mecanica/universitario/vetores/