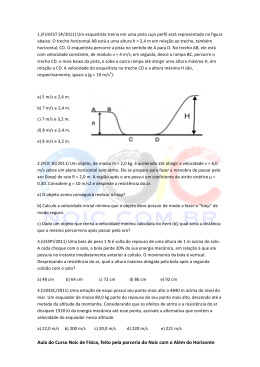
Energia Mecânica – Sistema Não Conservativo
1. (Unicamp 2013) Em agosto de 2012, a NASA anunciou o pouso da sonda Curiosity na superfície de Marte. A
sonda, de massa m = 1000 kg, entrou na atmosfera marciana a uma velocidade v0 = 6000 m/s.
a) A sonda atingiu o repouso, na superfície de Marte, 7 minutos após a sua entrada na atmosfera. Calcule o módulo
da força resultante média de desaceleração da sonda durante sua descida.
b) Considere que, após a entrada na atmosfera a uma altitude h0 = 125 km, a força de atrito reduziu a velocidade da
sonda para v = 4000 m/s quando a altitude atingiu h =100 km. A partir da variação da energia mecânica, calcule o
trabalho realizado pela força de atrito neste trecho. Considere a aceleração da gravidade de Marte, neste trecho,
constante e igual a gMarte = 4 m/s2.
2. (Ufpe 2012) Um objeto de 2,0 kg é lançado a partir do solo na direção vertical com uma velocidade inicial tal que o
mesmo alcança a altura máxima de 100 m. O gráfico mostra a dependência da força de atrito Fa , entre o objeto e o
meio, com a altura. Determine a velocidade inicial do objeto, em m/s. A aceleração da gravidade é g = 10 m/s2.
3. (Pucrj 2010) Um carrinho de montanha-russa percorre um trecho horizontal (trecho 1) sem perda de energia, à
velocidade de v1 = 36 km/h. Ao passar por uma pequena subida de 3,75 m, em relação ao trecho horizontal anterior, o
trem diminui sua velocidade, que é dada por v2 no ponto de maior altitude. Ao descer desse ponto mais alto, o carrinho
volta a se movimentar em um novo trecho horizontal (trecho 2) que é 1,8 m mais alto que o trecho horizontal 1. A
velocidade do carrinho ao começar a percorrer este segundo trecho horizontal é dada por v3. Nesse instante as rodas
do carrinho travam e ele passa a ser freado (aceleração a) pela força de atrito constante com os trilhos. O carrinho
percorre uma distância d = 40 m antes de parar. A aceleração da gravidade é g = 10 m/s2.
a) Calcule v2.
b) Calcule v3.
c) Calcule a aceleração de frenagem a devida ao atrito.
d) Em quanto tempo o carrinho conseguiu parar?
A figura abaixo representa a situação descrita.
4. (Fgv 2008) Ao passar pelo ponto A, a uma altura de 3,5 m do nível de referência B, uma esfera de massa 2 kg, que
havia sido abandonada de um ponto mais alto que A, possui velocidade de 2 m/s. A esfera passa por B e, em C, a 3,0
m do mesmo nível de referência, sua velocidade torna-se zero. A parcela de energia dissipada por ações resistentes
sobre a esfera é, em J,
Dado: g = 10 m/s2
a) 10.
b) 12.
c) 14.
d) 16.
e) 18.
5. (Uepb 2013) Uma família decide ir, no final de semana, ao Beach Park, que está localizado no Município de
Aquiraz, na praia do Porto das Dunas, no Ceará, a 16 km de Fortaleza. Uma das atrações para o público é o
Toboágua Insano, com 40 metros de altura, que tem a dimensão vertical de um prédio de 14 andares.
Em função da sua altura e inclinação, o toboágua proporciona uma descida extremamente rápida. Por essas
características, o Insano é considerado o mais radical dos equipamentos do gênero no planeta.
Numa manhã de domingo, um jovem, membro da família que foi visitar o parque, desce, a partir do repouso, o
toboágua, com altura de 40 metros de altura, e mergulha numa piscina instalada em sua base. Supondo que o atrito
ao longo do percurso dissipe 28% da energia mecânica e considerando a aceleração da gravidade, g = 10 m/s2, a
velocidade do jovem na base do toboágua, em m/s, é
a) 28,2
b) 26,4
c) 20,2
d) 24,0
e) 32,2
6. (Pucrj 2012) Uma bola de borracha de massa 0,1 kg é abandonada de uma altura de 0,2 m do solo. Após quicar
algumas vezes, a bola atinge o repouso. Calcule em joules a energia total dissipada pelos quiques da bola no solo.
Considere g = 10 m/s2.
a) 0,02
b) 0,2
c) 1,0
d) 2,0
e) 3,0
7. (Ucs 2012) O ato de escrever palavras numa folha de papel, usando o grafite de um lápis, e o ato de apagar essas
palavras, usando uma borracha, fisicamente envolvem a ideia de trabalho e força de atrito e, consequentemente, de
energia na forma de calor. Com base apenas na relação entre o grafite e o papel, e entre a borracha e o papel, podese afirmar que
a) escrever absorve calor do ambiente e apagar entrega calor ao ambiente.
b) tanto escrever quanto apagar são processos energeticamente reversíveis.
c) escrever e apagar entregam calor ao ambiente.
d) escrever e apagar absorvem calor do ambiente.
e) o trabalho realizado para escrever envolve força de atrito cinético zero.
8. (Uem 2012) Sobre a energia mecânica e a conservação de energia, assinale o que for correto.
01) Denomina-se energia cinética a energia que um corpo possui, por este estar em movimento.
02) Pode-se denominar de energia potencial gravitacional a energia que um corpo possui por se situar a uma certa
altura acima da superfície terrestre.
04) A energia mecânica total de um corpo é conservada, mesmo com a ocorrência de atrito.
08) A energia total do universo é sempre constante, podendo ser transformada de uma forma para outra; entretanto,
não pode ser criada e nem destruída.
16) Quando um corpo possui energia cinética, ele é capaz de realizar trabalho.
www.nsaulasparticulares.com.br
Página 2
Gabarito:
Resposta da questão 1:
a) Dados: m = 1000 kg; v0 = 6000 m/s; v = 0; Δt = 7 min = 420 s.
Da segunda lei de Newton, para a força resultante tangencial:
v
0  6000
6  106
Fres  m a  Fres  m
 1000


t
420
4,2  102
Fres  1,43  104 N.
b) Dados: m = 1000 kg; h0 = 125 km = 125  103 m; h = 100 km = 100  103 m; v = 4000 m/s; v0 = 6000 m/s; gMarte = 4
m/s2.
Sendo W Fat o trabalho da força de atrito, aplicando o Teorema da Energia Mecânica:

 m v2
  m v 02
final
inicial
WFat  EMec
 EMec
 WFat  
 m gMarteh   
 m gMarteh0  
 2
  2


 

m 2
2
WFat 
v  v 0  m gMarte h  h0  
2
1000
WFat 
40002  60002  1000  4 100  125   1000 
2





WFat  500 2  107

 4  106  25   1 1010  1 108

WFat  1,01 1010 J.
Resposta da questão 2:
Como há atuação da força de atrito, haverá energia dissipada no sistema. Devido a isso, podemos concluir que a
energia mecânica inicial será igual à energia mecânica final somada ao módulo do trabalho da força de atrito, que
representa a energia dissipada.
Eminicial  Emfinal  | τatrito |
- No momento inicial:
Eminicial  Ep  Ec  Eminicial  m.g.h 
h  0  Eminicial 
m.V02
2
m.V02
2
- No momento final:
Emfinal  Ep  Ec  Emfinal  m.g.h 
m.V 2
2
V  0  Emfinal  m.g.h
- Trabalho da força de atrito:
τatrito  área sob a curva do gráfico.
A figura sob a curva do gráfico é um triângulo e sua área será:
b.a 100.10
área 

 500
2
2
| τatrito | 500J
Eminicial  Emfinal  | τatrito |
m.V02
 m.g.h  500
2
Substituindo os valores:
m.V02
2.V02
 m.g.h  500 
 2.10.100  500
2
2
V0  50m / s
www.nsaulasparticulares.com.br
Página 3
Resposta da questão 3:
Dados: v1 = 36 km/h = 10 m/s; h2 = 3,75 m; h3 = 1,8 m; d = 40 m; g = 10 m/s2.
A figura abaixo representa a situação descrita.
a) Pela conservação da energia mecânica:
A
B
EMec
 EMec
v2 =

m v12 m v 22

 m g h2  v12  v22  2 g h2 
2
2
v2  v12  2 g h2 
102  2(10)(3,75)  25  v2 = 5 m/s.
b) Usando novamente a conservação da energia mecânica:
A
c
EMec
 EMec
v3 =

m v12 m v32

 m g h3  v12  v32  2 g h3 
2
2
v3  v12  2 g h3 
102  2(10)(1,8)  64  v3 = 8 m/s.
c) Como o carrinho para em D, v4 = 0.
Aplicando a equação de Torricelli no trecho CD, vem:
v 24  v 32  2 a d  0 = 8 + 2 a 40  – 80 a = 64  a = – 0,8 m/s .
2
2
d) Da função horária da velocidade:
v4 = v3 + a t  0 = 8 – 0,8 t  t 
8
 t = 10 s.
0,8
Resposta da questão 4:
[C]
Tomando B como referência:
1
1
mV 2  2x10x3,5  x2x22  74J
2
2
 mghB  2x10x3,0  60J
EtA  mghA 
EtB
Energia dissipada = 74 - 60 = 14J.
www.nsaulasparticulares.com.br
Página 4
Resposta da questão 5:
[D]
Se 28% da energia mecânica são dissipados na descida, a energia mecânica final é 72% da energia mecânica inicial.
Pelo Teorema da Energia Mecânica para sistemas não-conservativos:
final
incial
EMec
 0,72 EMec

m v2
 0,72 m g h  v  2  0,72  10  40  576 
2
v  24,0 m / s.
Resposta da questão 6:
[B]
A energia total dissipada é igual a energia potencial gravitacional inicial da bola.
Edissip  Epot  m g h  0,1 10  0,2  Edissip  0,2 J.
Resposta da questão 7:
[C]
Tanto escrever como apagar envolvem dissipação de energia mecânica, liberando energia na forma de calor para o
meio ambiente.
Resposta da questão 8:
01 + 02 + 08 + 16 = 27.
01) Correta. Energia cinética é energia mecânica associada ao movimento.
02) Correta. Energia potencial gravitacional é energia mecânica de posição, dependendo, portanto, da altura em
relação ao plano horizontal de referência.
04) Incorreta. A força de atrito pode atuar tanto como força dissipativa (transformando energia mecânica em térmica)
ou como força incrementativa (transferindo energia mecânica ao corpo).
08) Correta. É o que afirma o princípio da conservação da energia.
16) Correta. De acordo com o teorema da energia cinética, o trabalho da resultante é igual à variação da energia
cinética. OBS: nessa afirmativa há uma imprecisão, pois em Física o trabalho é realizado pela força que o corpo aplica
e não pelo corpo.
www.nsaulasparticulares.com.br
Página 5