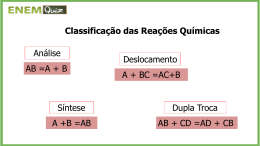
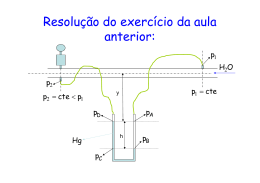
Segunda aula de
laboratório
27/08/2008
Para que ocorra um bom aproveitamento é
fundamental que não se tenha nenhuma
dúvida do passado.
re s trição do
capítulo
contínuo
f luido
incompressív el
em repouso
pressão
peso específ ico
conce ito
pressão em um
ponto f luido
escala ef etiv a
escala absoluta
Síntese da 1ª aula
27/8/2008 - v2
det. a v ariação de
pressão no trecho
de A = cte e com L
e xe rcício
te ore m a de Ste vin
Resolução do exercício:
determinação da diferença
de pressão entre as seções
(1) e (2), que para a foto a
seguir tem vazão igual a
zero.
Para a vazão nula tem-se:
p1  p2  0
p2
p1
Ao se colocar a vazão máxima, cria-se um
desnível como mostra o excelente esboço
elaborado pelo Bruno Oliveira Chen
Resoluçãopelo teoremade Stevin:
p3  p1  H2O  x  h  (A)
p3  p4  0  p3  p4  (B)
p4  p5  H g  h  (C)
p5  p2  H2O  x  (D)
De (C )  (D)  p4  p2  H g  h  H2O  x  (E)
De (B) em (E)  p3  p2  H g  h  H2O  x  (F)

De (f) - (A)  p1  p2  h  H g  H2O

Existe uma maneira bem
mais simples de se resolver
o exercício anterior, é pela
equação manométrica
É a equação que aplicada nos
manômetros de coluna de líquidos,
resulta em uma diferença de pressão
entre dois pontos fluidos, ou na
pressão de um ponto fluido.
Para se obter a equação manométrica,
deve-se adotar um dos dois pontos
como referência. Parte-se deste ponto,
marcando a pressão que atua no
mesmo e a ela soma-se os produtos
dos pesos específicos com as colunas
descendentes (+S*hdescendente), subtraise os produtos dos pesos específicos
com as colunas ascendentes (S*hascendente) e iguala-se à pressão que
atua no ponto não escolhido como
referência.
Aplicando-se a equação manométrica ao
esboço elaborado pelo Bruno Oliveira Chen
Adotando- se como referênciao ponto (1) :
p1  x * H2O  h * H2O  h * H g  x * H2O  p2

p1  p2  h * H g  H2O

Exemplo de aplicação
Gabarito
a) p1abs  H2O * 0,3  H g * 0,3  p2abs
p1abs  2,622 * 104  13600 * 0,3  1000 * 0,3
p1abs  30000
kgf
2
(abs)
m
patm  p1abs  p1efetiva  30000  20000
kgf 10000
patm  10000

 1000  735,3mmHg
2
13600
m
b) V1 
V1 
m1  R  T1 0,21  287  313

 0,064165m3
p1
30000  9,8
  D12
4
 0,5  D1 
4  0,064165
 0,4042m  404,2mm
  0,5
Outro exemplo de aplicação
Gabarito
Exercícios propostos do livro
do Prof. Franco Brunetti
2.5 (pg. 50 e 51), 2.6 (pg.
51), 2.8 (pg. 51 e 52), 2.10
(pg. 52), 2.11 (pg. 52 e 53)
e 2.16 (pg. 54 e 55)