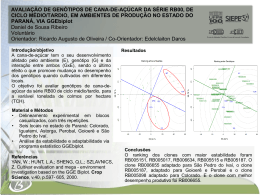
Modelagem da interação genótipos × ambientes com múltiplos
atributos
Lúcio Borges de Araújo1
Mirian Fernandes Carvalho Araújo1
Carlos Tadeu dos Santos Dias2
1 Introdução
Os ensaios multiambientais são conduzidos para estimar a estabilidade genotípica,
avaliar a performance dos genótipos em diferentes condições ambientais e quantificar e
interpretar a interação genótipo × ambiente (IGA), para que seja possível selecionar os
melhores genótipos que serão recombinados e plantados em outros anos e outros ambientes
no próximo ciclo de seleção. Vários modelos estatísticos são usados para avaliar o
comportamento dos genótipos; entre os mais recentemente propostos, estão os baseados na
decomposição em termos multiplicativos dos resíduos da IGA. Entre esses modelos
estatísticos, destaca-se o modelo com efeitos principais aditivos e efeito de interação
multiplicativa (AMMI)[4]
Uma descrição do ajuste de mínimos quadrados dos modelos AMMI é feito por [3].
Este autor estimou primeiramente os efeitos aditivos do modelo e depois fez a decomposição
em valores singulares da matriz (Z) de resíduos de interação. Os resultados podem ser
apresentados e interpretados por meio de um gráfico Biplot que reflete em dimensão reduzida
os aspectos mais relevantes da interação genótipo × ambiente.
Na maioria dos ensaios multiambientais, o geneticista faz avaliações de múltiplos
atributos e precisa selecionar os melhores genótipos levando em conta sua adaptabilidade e
performance no conjunto de variáveis. Com os modelos AMMI é possível estudar o
comportamento dos genótipos levando em conta um único atributo. No entanto, para obter
uma resposta completa, que considera todos os atributos, é preciso aplicar uma técnica
estatística que permita trabalhar com dados com uma estrutura tridimensional.
A Análise de Componentes Principais de três modos (ACP3) foi proposta inicialmente
por [7] ara estudos psicométricos, mas este procedimento também foi usado para estudar a
IGA com múltiplos atributos ([1] e [2]). Outras aplicações destes métodos foram feitas por
1
2
FAMAT – UFU. e-mail: [email protected]
LCE – ESALQ/USP.
1
[8] e por [9] para estudar a interação tripla em experimentos agrícolas onde os genótipos são
testados em diferentes locais durante vários anos.
Neste trabalho usa-se a Análise de Componentes Principais de três modos para
representar em dimensão reduzida as características mais importantes dos dados num ensaio
com 36 genótipos de milho, testados em 4 regiões do Brasil e onde foram avaliados 10
atributos. Primeiramente foi estudada a IGA com múltiplos atributos, usando o modelo
AMMI com múltiplos atributos como descrito.
2 Material e métodos
Os dados são provenientes de um experimento com 36 genótipos de Milho (primeiro
modo) (i=1,...,36), avaliados em 4 locais de Brasil (S1: Rio Branco-AC, S2: Milagres-CE, S3:
Linhares-ES, no solo Latossolo Amarelo Coeso, S4: Linhares-ES, no solo LVA-DistroficoLVD11) (segundo modo) (j=1,...,4). Em cada um dos ensaios foram avaliadas 10 variáveis:
X1: Florescimento (dias), X2: Altura da planta (cm), X3: Tamanho da espiga (cm), X4:
Porcentagem de plantas acamadas, X5: Porcentagem de plantas quebradas, X6: Stand final,
X7: Número de espigas, X8: porcentagem de espigas doentes, X9: Peso das espigas (kg/ha),
X10: Peso de grãos (kg/ha) (terceiro modo K=1.....10).
Para cada variável (atributo) foram calculadas as estimativas de resíduos de interação
dupla para o modelo AMMI (yij. – yi..- y.j. + y...), em que yij. representa a média da variável para
o genótipo i no local j; yi.. representa a média da variável para o genótipo i; y.j. representa a
média da variável no local j e y... representa a média geral dos dados. Logo foi formado um
arranjo de três entradas Zijk com os resíduos obtidos, em que o valor zijk representa o resíduo
para o genótipo i e local j, para a variável k. Então foi aplicada uma Análise de Componentes
Principais de três modos.
O método consiste em encontrar estimativas de mínimos quadrados do modelo de
P
Q
R
Tucker: z ijk .   aip b jq c kr g pqr , em que aip , bjq e ckr são os elementos das matrizes de
p 1 q 1 r 1
Componentes Principais (A, B e C) associada a cada modo respectivo, sendo que para o
conjunto de dados utilizado neste trabalho, A representa a matriz de componentes principais
para o modo genótipo, B representa a matriz de Componentes Principais para o modo local e
C representa a Matriz de Componentes Principais para o modo variável. G é um arranjo de
três entradas em que o elemento gpqr representa a relação entre o p-ésimo componente do
primeiro modo com o q-ésimo componente do segundo modo com o r-ésimo componente r do
2
terceiro modo. P é o posto da matriz Z1, 23 . Nesta matriz as linhas representam os níveis dos
genótipos e as colunas representam combinações dos níveis de locais e variáveis . Da mesma
maneira definem-se os valores Q e R como o posto das matrizes Z 2,13 e Z 3,1 2 .
Para a seleção do número de componentes principais a serem retidas em cada modo foi
utilizado o algoritmo proposto por [6], que se baseia em eliminações sucessivas até encontrar
a solução ótima.
A visualização do resultado foi feita por meio do gráfico joint biplot, que é uma
representação simultânea de dados contidos num arranjo de três entradas. Para obter este
gráfico é preciso projetar as componentes de dois fatores sobre as componentes principais de
outro fator. Este procedimento é descrito por [5].
3 Resultados e discussões
A solução 6 × 2 × 3, obtidos ao aplicar uma Análise de Componentes Principais de
três modos ao arranjo de três vias, explica 44,92 % da variabilidade total dos dados. Os
componentes do modo genótipo explicam respectivamente 12,85 %, 11,70 %, 6,37 %, 6,22
%, 4,93 % e 2,84 %, as componentes do modo locais explicam respectivamente 25,49 % e
19,44 % e as componentes do modo atributo explicam 22,6 %, 11,6 % e 11,0 % da
variabilidade total.
O componente 1 do modo Local está caracterizado por todos os locais com pesos
relativamente altos (Matriz C tabela 1). Este componente contrapõe-se aos locais S1 e S2 (Rio
Branco-AC e Milagres-CE) dos locais S3 e S4 (Linhares-ES solo Latossolo Amarelo Coeso e
Linhares-ES solo LVA- distrófico -LVD11).
O gráfico da Figura 1 mostra as interações mais importantes entre genótipos × locais
para o conjunto dos atributos avaliados; as mesmas apresentam-se na variável X4
(porcentagem de plantas acamadas). O genótipo 19 interatua positivamente nos locais S1 e S2
e negativamente nos locais S3 e S4 para esta variável. Os genótipos 18 e 31 têm um
comportamento totalmente contrário ao genótipo 19, ou seja interatuam positivamente nos
locais S3 e S4 e interatuam negativamente nos locais S1 e S2 para o atributo X4. Em relação à
variável X2 (Altura da planta) o comportamento destes genótipos é totalmente contrário a
variável X4); ou seja, o genótipo 19 interatua negativamente nos locais S1 e S2 e positivamente
nos locais S3 e S4 para a variável X2.
3
Figura 1: Biplot de projeção sobre a primeira Figura 2: Biplot de projeção sobre a segunda
componente do modo local para modelo componente do modo local para modelo
AMMI.
AMMI.
Na Figura 1 destaca-se também, a contraposição entre os genótipos 9 e 12 dos
genótipos 17, 24 e 32. O primeiro grupo interatua positivamente nas variáveis X6, X9 e X10
para os locais S1 e S2 e negativamente nestes mesmos atributos para os locais S3 e S4. Os
genótipos 17, 24 e 32 têm interação positiva nos atributos X1 e X8 nas locais S1 e S2 mais tem
interação negativa nos locais S3 e S4 nestes mesmos atributos.
Na Figura.2 apresentam-se o Biplot de projeção sobre o segundo componente dos
locais caracterizado pela contraposição entre os locais S1 e S2 com pesos respectivos (-0.75 e
0.64) (Matriz C, tabela.1). Então nesta representação gráfica é possível estudar as interações
duplas genótipos × locais nos diferentes atributos para os locais S1 e S2. O genótipo 15
interatua positivamente no local S1 para a variável X7 e interatua negativamente na local S2
para este mesmo atributo. Destacam-se além disso a contraposição dos genótipos 4 e 18 do
genótipo 26, o genótipo 26 tem interação positiva no atributo X4 para a local S1 e tem
interação negativa no local S2 para este mesmo atributo. Podem ser observadas também a
contraposição dos genótipos 5 e 14 dos genótipos 6 e 36 para as variáveis X6, X9 e X10. O
primeiro grupo interage positivamente no local S2 e negativamente no local S1.
4 Conclusões
Baseados na Análise de Componentes Principais de Três Modos é possível trabalhar
simultaneamente com múltiplos atributos no ajuste dos modelos AMMI; por tanto pode-se
estudar de forma multivariada os aspectos mais importantes da interação genótipo ambiente e
da resposta dos genótipos nas diferentes condições ambientais.
4
No caso de ter muitas combinações de níveis nos fatores, os Biplots de projeções
constituem uma poderosa ferramenta para representar três matrizes de marcadores, permitindo
dar uma interpretação mais esclarecedora dos aspectos mais importantes da resposta dos
genótipos.
Foi possível detectar as combinações de genótipos × locais × variáveis responsáveis da
interação e da resposta diferenciada permitindo identificar os melhores genótipos tendo em
conta sua adaptabilidade e performance.
5 Referências
[1] BASFORD, K.E.; KROONENBERG, P.M.; DELACY, I.H.; LAWRENCE, P.K.
Multiattribute evaluation of regional cotton variety trials. Theoretical and Applied Genetics,
v.79, p.225-324, 1990.
[2] CROSSA, J.; BASFORD, K.E.; TABA, S.; DELACY, I.H; SILVA, E. Three mode
analysis of maize using morphological and agronomic attributes measured in multilocation
trials. Crop Science, v.35, p.1483-1491, 1995.
[3] GABRIEL, K.R. The Biplot graphic display of matrices with applications to principal
components analysis. Biometrika, v.58, p.453-467, 1971.
[4] GAUCH, H.G. Model Selection and Validation for Yield Trials with Interaction.
Biometrics, v.44, p.705-715, 1988.
[5] KROONENBERG, P.M.; DE LEEUW, J. Principal Component Analysis of Three-Mode
Data by means of Alternating Least Squares Algorithms. Psychometrika, v.45, p.69-97,
1980.
[6] TIMMERMAN, M.E.; KIERS, H.A.L. Three-mode principal components analysis.
Choosing the number of components and sensitivity to local optima. British Journal of
Mathematical and Statistical Psychology, v.53: p.1-16, 2000.
[7] TUCKER, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika,
v.31, p.279-311, 1966.
[8] VAN EEUWIJK, F.A.; KROONENBERG, P.M. Multiplicative Models for Interaction in
Three-Way ANOVA, with Applications to Plant Breeding. Biometrics, v.54, p.1315-1333,
1998.
[9] VARELA, M., CROSSA, J.; JADISH, R.; ARUN, K.; TRETHOWAN, R. Analysis of
three way interaction including multi-attributes. Australian Journal of Agricultural
Research, v.57, p.1185-1183, 2006.
5