7. Medida de associação entre duas variáveis quantitativas
Considere duas variáveis aleatórias X e Y observadas
conjuntamente. Então, uma amostra bivariada de tamanho n, de
pares (X, Y), é dada por:
(x1, y1), (x2, y2), (x3, y3), . . . , (xn, yn).
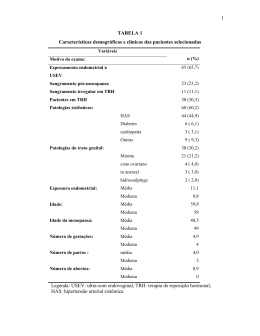
Uma forma de representar graficamente os valores observados
é através de um gráfico de pontos no plano cartesiano, por meio
do qual podemos verificar se existe alguma relação entre X e Y,
como por exemplo, uma relação linear (uma reta), conforme
Figura 7.1.
Figura 7.1: Plano cartesiano com pares de pontos (x, y), com
relação linear aproximada.
Muitas vezes, na análise de dados, temos o interesse em
avaliar o comportamento linear da associação entre duas variáveis
quantitativas.
Uma forma de medir o grau da associação linear entre duas
variáveis quantitativas é dada pelo coeficiente de correlação de
Pearson, denotado por  xy e definido por
 xy  Cor ( X , Y ) 
Cov ( X , Y )
,
Var( X )Var(Y )
em que, Cov( X , Y ) é uma medida de variação conjunta de X e Y,
chamada de covariância.
7.1. O coeficiente de correlação amostral
Sejam duas variáveis aleatórias X e Y, observadas
conjuntamente. Para definirmos o coeficiente de correlação
amostral, primeiramente vamos definir a covariância amostral
entre X e Y:
sxy 
 ( xi  x )( yi  y ) .
n 1
Com um pouco de álgebra, mostra-se que a expressão acima
pode ser escrita como
sxy 
 xi yi  n x y .
n 1
Desta forma, o coeficiente de correlação amostral rxy é
definido por:
rxy 
rxy 
 ( xi  x )( yi  y )
,
2
2
 ( xi  x )  ( yi  y )
 xi yi  n x y
( xi2  nx 2 ) ( yi2  ny 2 )
Ou seja,
sxy
,
rxy 
sx s y
em que s x e s y são os desvios padrões amostrais de X e Y,
respectivamente.
Exemplo 7.1: Sejam os dados:
x
y
2
11
3
15
5
13
5
18
7
17
8
16
Logo, n = 6 e
i)
x
30
 5,
6
2
 xi  176 e
2
2
 xi  nx  176  6  25  26

sx2 
26
 5.2
5
ii) y 
90
 15
6
2
 yi  1384 e
2
2
 yi  ny  1384  6  225  34
iii)  xi yi  469
sxy 

s y2 
34
 6.8
5
 xi yi  n x y  469  6  5 15  19 e
19
 3.8
5
Desta forma:
rxy 
3.8

5.2  6.8
19
 0.639
26  34
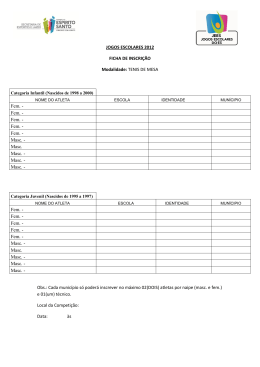
Figura 7.2: Representação dos dados do exemplo.
Comandos no R:
> x <- c(2,3,5,5,7,8)
> y <- c(11,15,13,18,17,16)
> sum(x)
[1] 30
> mean(x)
[1] 5
> sum(x^2)
[1] 176
> var(x)
[1] 5.2
> sum(y)
[1] 90
> mean(y)
[1] 15
> sum(y^2)
[1] 1384
> var(y)
[1] 6.8
> sum(x*y)
[1] 469
> cov(x,y)
[1] 3.8
> rxy <- cov(x,y)/sqrt(var(x)*var(y))
> rxy
[1] 0.6390392
> cor(x,y)
[1] 0.6390392
Notas:
i) O coeficiente de correlação varia ente −1 e 1;
Se a relação entre X e Y é linear, do tipo Y = aX + b, então
 rxy é igual a 1 se a > 0 (inclinação positiva);
 rxy é igual a −1 ser a < 0 (inclinação negativa);
ii) quanto mais os pontos se aproximam de uma linha reta, mais
rxy se aproxima de 1 (ou −1).
iii) Assim, podemos classificar a relação entre X e Y em função
da magnitude do coeficiente de correlação amostral:
Valor de rxy
| rxy | = 1
0.90 ≤ | rxy | < 1
0.70 ≤ | rxy | < 0.90
0.40 ≤ | rxy | < 0.70
0.20 ≤ | rxy | < 0.40
0 ≤ | rxy | < 0.20
Classificação
correlação perfeita
correlação muito forte
correlação forte
correlação moderada
correlação fraca
correlação muito fraca
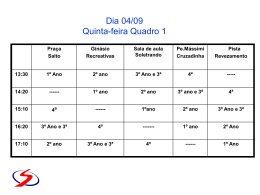
Exemplo 7.2: Coeficiente de correlação linear para n = 200 pares
de pontos (x, y), calculado no R.
rxy  1.0
rxy  0.939
rxy  0.770
rxy  0.528
rxy  0.331
rxy  0.048
7.2. Interpretação geométrica do coeficiente de correlação
amostral
Considere n, de pares (x1, y1), (x2, y2), (x3, y3), . . . , (xn, yn).
Então, x = (x1, x2, x3, . . . , xn) e y = (y1, y2, y3, . . . , yn) podem
ser considerados dois vetores no espaço n-dimensional.
Seja o ângulo entre os vetores x e y, mostra-se por meio do
produto escalar entre x e y, corrigidos pelas suas respectivas
médias amostrais x e y , que o cosseno de  é dado por:
cos() 
 ( xi  x )( yi  y )
,
2
2
 ( xi  x )  ( yi  y )
ou seja, cos()  rxy .
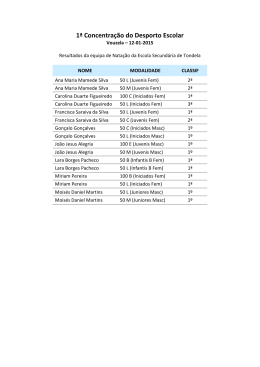
Exemplo 7.3: Sejam os dados (2, 6), (4, 8), (6, 7), então, x  4 e
y  7 . Logo (x  x)  (2, 0, 2) e (y  y )  (1, 1, 0) .
Como, o cosseno do ângulo entre os vetores x  (2, 4, 6) e
y  (6, 8, 7) é dado por:
Figura 7.3: Representação dos vetores x e y no espaço 3D.
cos() 
( x  x) t ( y  y )
.
t
t
(x  x) ( x  x) ( y  y ) ( y  y )
Mas: (x  x)t (y  y )   ( xi  x )( yi  y )
(x  x)t (x  x)   ( xi  x )2
(y  y )t (y  y )   ( yi  y )2
Então, cos() 
 ( xi  x )( yi  y )
 rxy
2
2
 ( xi  x )
 ( yi  y )
No exemplo, temos que:
(2, 0, 2)t (2, 0, 2)  8
(1, 1, 0)t (1, 1, 0)  2
(2, 0, 2)t (1, 1, 0)  2
Portanto, cos() 
2
1

8 2
2
  arcos(0.5)  60
De fato, cor(X, Y) = 0.5
## cálculo da correlação no R
#############################
x <- c(2,4,6)
y <- c(6,8,7)
cor(x,y)
[1] 0.5
Comandos do Maple para representação dos vetores.
with(plots):
x := arrow(`<,>`(2, 4, 6), shape = arrow, color = red);
y := arrow(`<,>`(6, 8, 7), shape = arrow, color = red);
display(x, y, scaling = CONSTRAINED);
Exemplo 7.4: Considere as medidas da qualidade do ar no
aeroporto de Nova Iorque.
Medidas diárias da qualidade do ar em Nova Iorque entre maio e
setembro de 1973.
O conjunto de dados é formado por 154 observações em 6
variáveis. Excluindo-se os dados perdidos (missing) este número
caiu para 111.
Descrição dos dados:
Leituras diárias das seguintes medidas de qualidade do ar no
período de 1 de maio a 30 de setembro de 1973.
i) Ozone: ozônio, em partes por bilhão;
ii) Solar.R: radiação solar em Langleys, na banda de frequência
de 4000–7700 Angstroms;
iii) Wind: velocidade media do vento em milhas por hora;
iv) Temp: tempartura máxima diária em graus Fahrenheit.
Fonte: Os dados foram obtidos do Departamento de Conservação
(Department of Conservation) e do Serviço Nacional de
Meteorologia (National Weather Service) de Nova Iorque.
require(graphics)
attach(airquality)
clima <- na.omit(data.frame(Solar.R,Ozone,Temp,Wind))
attach(clima)
cor(Temp,Ozone)
[1] 0.6985414
cor(Wind,Ozone)
[1] -0.6124966
cor(Wind,Solar.R)
[1] -0.1271835
7.3. Relações não lineares
O coeficiente de correlação linear é uma medida da
correlação linear entre duas variáveis X e Y, não sendo indicado
quando a relação não for linear (como por exemplo, quadrática).
No entanto, devido à disposição dos pontos no plano
cartesiano, uma relação não linear pode resultar num coeficiente
de correlação alto, indicando falsamente a existência de uma
relação linear entre as variáveis.
Exemplo 7.4: Considere os dois casos abaixo.
Caso 1: relação quadrática.
x
y
x
y
26.03 26.79 27.02 27.58 25.19 24.37 24.77 25.01 27.40
2330.4 2434.0 2650.5 4784.2 1208.1 1210.6 1087.1 1492.8 4291.2
22.40 25.82
868.1 1843.2
23.66 25.81 27.12 26.88
964.5 1429.7 4403.6 4273.6
22.82
711.3
23.25 25.52
753.0 1308.8
Apesar da associação quadrática, o coeficiente de correlação
linear é muito alto: rxy  0.8506 .
x <- c(26.03,26.79,27.02,27.58,25.19,24.37,24.77,
25.01,27.40,22.40,25.82,23.66,25.81,27.12,
26.88,22.82,23.25,25.52)
y <- c(2330.4,2434.0,2650.5,4784.2,1208.1,1210.6,
1087.1,1492.8,4291.2, 868.1,1843.2, 964.5,
1429.7,4403.6,4273.6, 711.3, 753.0,1308.8)
cor(x,y)
[1] 0.8506397
Caso 2: relação exponencial:
x 90.0 92.1 148.4 315.0 286.3
y
8
5
3
1
2
x 142.6 190.7 145.3 76.4 228.7
y
4
2
5
9
2
72.6
7
91.7
6
184.7 249.1
3
1
244.0 232.1
2
1
70.5
8
94.2
7
Apesar da associação exponencial, o coeficiente de
correlação linear é muito alto: rxy  0.9068
x <- c( 90.0, 92.1,148.4,315.0,286.3, 72.6,184.7,
249.1, 70.5,142.6,190.7,145.3, 76.4,228.7,
91.7,244.0,232.1, 94.2)
y <- c(8,5,3,1,2,7,3,1,8,4,2,5,9,2,6,2,1,7)
cor(x,y)
[1] -0.9068605
74. Matriz de correlações amostrais
Quando temos várias variáveis para serem analisadas e
pretendemos calcular todas as correlações duas-a-duas, uma
forma bastante prática de representa-las é através de uma matriz.
A matriz de correlações amostrais é denotada por R,
tendo as correlações representadas nos cruzamentos das linhas
com as colunas.
A matriz de correlações amostrais R apresenta as seguintes
características:
i) os elementos da diagonal de R são iguais a 1 uma vez que a
correlação de uma variável consigo mesma é 1;
ii) a matriz R é simétrica, pois para duas variáveis quaisquer Xi
e Xj :
cor ( X i , X j )  cor ( X j , X i ) ;
iii) os elementos de R fora da diagonal são valores entre −1 e 1.
Exemplo: matriz de correlações 44.
1
R = cor(X2, X1)
cor(X3, X1)
cor(X4, X1)
cor(X1, X2)
1
cor(X3, X2)
cor(X4, X2)
cor(X1, X3)
cor(X2, X3)
1
cor(X4, X3)
cor(X1, X4)
cor(X2, X4)
cor(X3, X4)
1
Exemplo 7.5: Dados da qualidade do ar em Nova Iorque.
# criando uma matriz de dados
#############################
clima <- cbind(Solar.R,Temp,Ozone,Wind)
cor(clima)
Solar.R
Temp
Ozone
Wind
Solar.R 1.0000000 0.2940876 0.3483417 -0.1271835
Temp
0.2940876 1.0000000 0.6985414 -0.4971897
Ozone
0.3483417 0.6985414 1.0000000 -0.6124966
Wind
-0.1271835 -0.4971897 -0.6124966 1.0000000
Exemplo 7.6: Dados dos alunos de Estatística 1 no primeiro
semestre de 2015. Calcular as correlações amostrais das variáveis
Tempo para chegar na UFScar, Idade, Peso e Altura.
dados <- read.table(choose.files(), head=T)
attach(dados)
# criando um data frame
#######################
dados.q <- data.frame(Tempo,Idade,Peso,Altura)
cor(dados.q, use="na.or.complete")
Tempo
Idade
Peso
Altura
Tempo
1.00000000 -0.09145379 0.01523087 0.04526220
Idade -0.09145379 1.00000000 0.18756244 0.09099185
Peso
0.01523087 0.18756244 1.00000000 0.66086059
Altura 0.04526220 0.09099185 0.66086059 1.00000000
8. Associação entre variáveis quantitativas e qualitativas
Sejam duas variáveis X e Y, observadas conjuntamente, sendo
uma delas quantitativa e a outra qualitativa. A associação
entre variáveis X e Y pode ser medida basicamente de duas
maneiras:
8.1. Categorizando a variável quantitativa
Categoriza-se a variável quantitativa em classes,
adequadamente escolhidas, e cruzam-se as duas variáveis numa
tabela de dupla entrada.
Neste caso, a associação é medida pelo 2 de Pearson e das
medidas de associação (coeficiente de contingência, coeficiente V
de Cramér, coeficiente ).
Exemplo 7.7: Levantamento da dados sobre o tipo de crimes pela
da idade do praticante (dados fictícios).
Variáveis observadas: idade (anos), crime (tipo de crime).
A variável idade foi categorizada nas seguintes faixas etárias:
 de 15 a 25 (incompletos);
 de 25 a 35 (incompletos);
 35 anos ou mais.
idade
21,
28,
35,
50,
22,
28,
37,
54,
<- c(16, 17, 17, 18, 18, 18, 18, 18, 19, 19, 19, 21, 21,
22, 22, 23, 23, 23, 23, 23, 24, 25, 25, 26, 26, 27, 27,
28, 29, 29, 29, 30, 30, 31, 31, 32, 33, 33, 34, 34, 34,
37, 37, 38, 39, 40, 40, 41, 42, 42, 43, 44, 45, 46, 48,
54)
crime <- c("Furto ou Roubo", "Furto ou Roubo", "Furto ou Roubo",
"Furto ou Roubo", "Latrocínio", "Latrocínio", "Latrocínio",
"Sequestro relâmpago", "Furto ou Roubo", "Furto ou Roubo",
"Sequestro relâmpago", "Furto ou Roubo", "Furto ou Roubo",
"Latrocínio", "Latrocínio", "Sequestro relâmpago", "Sequestro
relâmpago", "Furto ou Roubo", "Latrocínio", "Sequestro relâmpago",
"Sequestro relâmpago", "Estelionato", "Furto ou Roubo", "Furto ou
Roubo", "Estelionato", "Latrocínio", "Estupro", "Latrocínio",
"Estupro", "Latrocínio", "Sequestro relâmpago", "Receptação",
"Furto ou Roubo", "Latrocínio", "Receptação", "Estupro",
"Receptação", "Estupro", "Estelionato", "Latrocínio",
"Latrocínio", "Sequestro relâmpago", "Furto ou Roubo", "Sequestro
relâmpago", "Estupro", "Sequestro relâmpago", "Furto ou Roubo",
"Estupro", "Estelionato", "Furto ou Roubo", "Receptação", "Furto
ou Roubo", "Receptação", "Estupro", "Receptação", "Receptação",
"Estupro", "Furto ou Roubo", "Estupro", "Estelionato",
"Receptação", "Estupro", "Estelionato", "Estelionato")
fx_etar <- c("15 a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15
a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15 a 25", "15 a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15
a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15 a 25-", "15 a 25", "15 a 25-", "15 a 25-", "25 a 35-", "25 a 35-", "25 a 35-", "25
a 35-", "25 a 35-", "25 a 35-", "25 a 35-", "25 a 35-", "25 a 35", "25 a 35-", "25 a 35-", "25 a 35-", "25 a 35-", "25 a 35-", "25
a 35-", "25 a 35-", "25 a 35-", "25 a 35-", "25 a 35-", "25 a 35", "25 a 35-", "25 a 35-", "35 ou mais", "35 ou mais", "35 ou
mais", "35 ou mais", "35 ou mais", "35 ou mais", "35 ou mais", "35
ou mais", "35 ou mais", "35 ou mais", "35 ou mais", "35 ou mais",
"35 ou mais", "35 ou mais", "35 ou mais", "35 ou mais", "35 ou
mais", "35 ou mais", "35 ou mais")
Tabelas de frequências das variáveis crime e faixa etária.
Crime
Furto ou roubo
Latrocínio
Estupro
Sequestro relâmpago
Receptação
Estelionato
Total
ni
17
12
10
10
8
7
64
Faixa etária
15 a 2525 a 3535 anos ou mais
Total
ni
23
22
19
64
# Histograma da variável idade (anos)
#####################################
br <- seq(15,57,by=6)
hist(idade, breaks=br, col="lightcoral", main="Idade
(anos)", xlab="", ylab="", axes=FALSE)
axis(2)
axis(1,br)
> tab <- table(crimes,fx_etar)
> tab
+----------------------------------+
|
fx_etar
|
+---------------------+----------+----------+------------+
| crimes
| 15 a 25- | 25 a 35- | 35 ou mais |
+---------------------+----------+----------+------------+
| Furto ou Roubo
|
10 |
3 |
4 |
| Latrocínio
|
6 |
6 |
0 |
| Sequestro relâmpago |
6 |
3 |
1 |
| Estelionato
|
1 |
2 |
4 |
| Estupro
|
0 |
5 |
5 |
| Receptação
|
0 |
3 |
5 |
+---------------------+----------+----------+------------+
> chisq.test(tab)
# Cálculo do X2
Pearson's Chi-squared test
data: tab
X-squared = 26.378, df = 10, p-value = 0.003264
Warning message:
In chisq.test(tab) : Chi-squared approximation may be
incorrect
Devido ao número excessivo de caselas da tabela com
frequências muito pequenas (menores do que 5), a análise pelo
quiquadro (X 2) não é válida (ver advertência, ou Warning
message).
Neste caso, podemos verificar uma evidência de associação
pelo gráfico de colunas, indicando que os crimes de furto ou
roubo, latrocínio e sequestro relâmpago são mais comuns na
faixa etária mais baixa e, os crimes de estelionato, estupro e
receptação são mais frequentes na faixa etária mais alta, vamos
calcular as medidas de associação.
Vamos utilizar o R para calcular os coeficientes de
contingência e V de Cramér. Para isso, é necessário carregar o
pacote vcd com o comando require(vcd).
require(vcd)
# carregando o pacote vcd
assocstats(tab) # commando para as medidas de associação
X^2 df
P(> X^2)
Likelihood Ratio 35.192 10 0.00011578
Pearson
26.378 10 0.00326359
Phi-Coefficient
: 0.642
Contingency Coeff.: 0.540
Cramer's V
: 0.454
Apresentação dos cálculos:
i) Coeficiente de contingência: t = min(6, 3) = 3
C
26.378

26.378  64
C*  0.540 
26.378

90.378
0.2919  0.540
3
 0.662
(3  1)
ii) Coeficiente V de Cramér:
V
26.378

2  64
79.134

128
0.2061  0.454
8.2. Comparando cada classe da variável qualitativa
Avalia-se a variável quantitativa individualmente para cada
uma das categorias da variável qualitativa, comparando-se os
resultados. A análise pode ser feita através das medidas
descritivas e graficamente (histogramas, box-plot’s, gráficos de
pontos).
Exemplo 7.8: Num estudo sobre a eficácia de inibidores de
ferrugem, quatro marcas (A, B, C, D) foram testadas. Ao todo, 40
corpos de prova foram distribuídos entre as quatro marcas, sendo
10 unidades para cada uma. Os 40 corpos de prova passaram por
um tratamento pelo respectivo inibidor e foram expostos à
severas condições de tempo. Os resultados são apresentados na
tabela 7.1: quanto maior o valor mais avaliado, mais eficaz é o
inibidor de ferrugem.
Tabela 7.1: Inibidores de ferrugem de 4 marcas.
Unidade Marca A
Marca B
Marca C
Marca D
43.9
59.8
53.4
36.2
1
39.0
57.1
54.3
45.2
2
46.7
62.7
53.5
40.7
3
43.8
60.6
51.4
40.5
4
44.2
57.7
55.0
39.3
5
47.7
62.4
53.1
40.3
6
43.6
56.1
55.6
43.2
7
38.9
58.1
50.2
38.7
8
43.6
60.8
48.8
40.9
9
40.0
59.1
54.2
39.7
10
Fonte: Neter, Wasserman, Kutner - Applied Linear Statistical Models,
IRWIN, 3rd Ed. (dados modificados).
A) No Minitab
Descriptive Statistics: Y
Variable
Corrosao
Marca
A
B
C
D
N
10
10
10
10
Mean
43.14
59.44
52.95
40.47
Variable
Corrosao
Marca
A
B
C
D
Skewness
-0.19
0.09
-0.87
0.39
Variance
9.00
4.92
4.70
5.94
CoefVar
6.95
3.73
4.10
6.02
Q1
39.75
57.55
51.10
39.15
Median
43.70
59.45
53.45
40.40
Kurtosis
-0.81
-1.08
-0.07
1.24
Marca
Gráfico de pontos de Corrosão x Marca
A
B
C
D
38.5
42.0
45.5
49.0
52.5
56.0
59.5
Corrosão
Boxplot de Corrosão
65
60
Corrosão
55
50
45
40
35
A
B
C
Marca
D
63.0
Q3
44.825
61.200
54.475
41.475
B) No R
Corrosao <- c(43.9,
43.6, 38.9, 43.6,
57.7, 62.4, 56.1,
53.5, 51.4, 55.0,
36.2, 45.2, 40.7,
40.9, 39.7)
39.0,
40.0,
58.1,
53.1,
40.5,
46.7,
59.8,
60.8,
55.6,
39.3,
43.8,
57.1,
59.1,
50.2,
40.3,
44.2,
62.7,
53.4,
48.8,
43.2,
47.7,
60.6,
54.3,
54.2,
38.7,
Marca <- factor(c(rep("A",10), rep("B",10),
rep("C",10), rep("D",10)))
boxplot(Corrosao ~ Marca, main="Box-plot de Corrosão
x Marca", xlab="Marca", ylab="Corrosão", pch=19,
col=c("red","blue","green","yellow2"), cex.main=1)
# construindo a matriz mCorrosao com os dados
#############################################
y1 <- Corrosao[which(Marca=="A")]
y2 <- Corrosao[which(Marca=="B")]
y3 <- Corrosao[which(Marca=="C")]
y4 <- Corrosao[which(Marca=="D")]
mCorrosao <- cbind(y1,y2,y3,y4)
dimnames(mCorrosao)[[2]] <- c("Marca A", "Marca B",
"Marca C", "Marca D")
mCorrosao
Marca A
[1,]
43.9
[2,]
39.0
[3,]
46.7
[4,]
43.8
[5,]
44.2
[6,]
47.7
[7,]
43.6
[8,]
38.9
[9,]
43.6
[10,]
40.0
Marca B
59.8
57.1
62.7
60.6
57.7
62.4
56.1
58.1
60.8
59.1
Marca C
53.4
54.3
53.5
51.4
55.0
53.1
55.6
50.2
48.8
54.2
Marca D
36.2
45.2
40.7
40.5
39.3
40.3
43.2
38.7
40.9
39.7
# calculando as medidas descritivas
###################################
xbar <- apply(mCorrosao, 2, mean)
vari <- apply(mCorrosao, 2, var)
cf.var <- 100*apply(mCorrosao, 2,
sd)/apply(mCorrosao, 2, mean)
Q1 <- apply(mCorrosao, 2, quantile)[2,]
mediana <- apply(mCorrosao, 2, median)
Q3 <- apply(mCorrosao, 2, quantile)[4,]
skew <- apply(mCorrosao, 2, skewness)
kurt <- apply(mCorrosao, 2, kurtosis)
# colocando as medidas descritivas numa tabela
##############################################
Descritivas <- rbind(xbar, vari, cf.var, Q1,
mediana, Q3, skew, kurt)
round(Descritivas,3)
# medidas descritivas calculadas no R
#####################################
Marca A
Marca B
Marca C
xbar
43.140
59.440
52.950
vari
9.000
4.920
4.703
cf.var
6.954
3.732
4.096
Q1
40.900
57.800
51.825
mediana
43.700
59.450
53.450
Q3
44.125
60.750
54.275
skew
-0.134
0.063
-0.628
kurt
-1.384
-1.506
-1.045
Marca D
40.470
5.936
6.020
39.400
40.400
40.850
0.282
-0.440
Exemplo 7.9: Analisar a associação entre as variáveis Altura e
Sexo dos alunos das turmas A e B de Estatística 1, primeiro
semestre de 2015.
Análises feitas pelo R:
Altura <- c(1.52,
1.60, 1.61, 1.63,
1.68, 1.68, 1.68,
1.72, 1.72, 1.73,
1.75, 1.75, 1.76,
1.79, 1.79, 1.80,
1.89, 1.90, 1.95)
1.55,
1.63,
1.69,
1.73,
1.77,
1.80,
1.57,
1.64,
1.70,
1.73,
1.77,
1.80,
1.58,
1.65,
1.70,
1.73,
1.78,
1.83,
1.59,
1.65,
1.70,
1.74,
1.78,
1.83,
1.60,
1.65,
1.70,
1.74,
1.78,
1.83,
1.60,
1.67,
1.70,
1.74,
1.79,
1.83,
Sexo <- c("Fem", "Fem", "Fem", "Fem", "Fem", "Fem",
"Fem", "Fem", "Fem", "Fem", "Masc", "Fem", "Fem",
"Masc", "Masc", "Fem", "Fem", "Fem", "Fem", "Fem",
"Masc", "Masc", "Fem", "Fem", "Masc", "Fem", "Masc",
"Fem", "Masc", "Fem", "Fem", "Masc", "Masc", "Masc",
"Masc", "Fem", "Masc", "Masc", "Masc", "Masc", "Masc",
"Fem", "Masc", "Masc", "Masc", "Masc", "Masc", "Masc",
"Masc", "Masc", "Masc", "Masc", "Masc", "Masc", "Masc")
Histograma de Altura.
1ª. Possibilidade:
A seguir vamos analisar a variável Altura comparando-a para
classe da variável Sexo.
# calculando as medidas descritivas
###################################
require(e1071)
# pacote para cálculo de
# assimetria e curtose
y1 <- Altura[which(Sexo=="Fem")]
y2 <- Altura[which(Sexo=="Masc")]
xbar <- c(mean(y1),mean(y2))
desv.pad <- c(sd(y1),sd(y2))
cf.var <- 100*desv.pad/xbar
Q1 <- c(quantile(y1)[2], quantile(y2)[2])
mediana <- c(median(y1),median(y2))
Q3 <- c(quantile(y1)[4], quantile(y2)[4])
skew <- c(skewness(y1), skewness(y2))
kurt <- c(kurtosis(y1), kurtosis(y2))
# colocando as medidas descritivas numa tabela
##############################################
Descritivas <- rbind(xbar, desv.pad, cf.var, Q1,
mediana, Q3, skew, kurt)
dimnames(Descritivas)[[2]] <- c("Feminino",
"Masculino")
round(Descritivas,4)
# medidas descritivas por Sexo, calculadas no R
###############################################
Feminino
Masculino
xbar
1.6552
1.7713
desv.pad
0.0681
0.0725
cf.var
4.1165
4.0945
Q1
1.6000
1.7325
mediana
1.6700
1.7750
Q3
1.7000
1.8000
Skew
-0.1238
0.2280
kurt
-1.0748
-0.0314
Podemos observar pelas médias amostrais dos dois grupos e
ainda, pelas medidas de posição (mediana e quartis) que os
homens apresentam uma altura cerca de 10cm superior às
mulheres. Resultado este, que pode ser visualizado pelos
diagramas de box-plots dos sexos feminino e masculino.
boxplot(Altura ~ Sexo, main="Box-plot de Altura x
Sexo", xlab="Sexo", ylab="Altura (m)", pch=19,
col=c("tomato", "lightseagreen"), cex.main=1)
2ª. Possibilidade:
Para os mesmos dados, vamos categorizar a variável Altura
numa variável qualitativa Estatura, cruzando-a com a variável
Sexo numa tabela de dupla entrada.
A variável Estatura será criada pela seguinte categorização da
variável Altura:
 Estatura Baixa: abaixo de 1.65m;
 Estatura Mediana: entre 1.65m e 1.80 m;
 Estatura Alta: 1.80 m ou mais.
Estatura <- c("Baixa", "Baixa", "Baixa", "Baixa",
"Baixa", "Baixa", "Baixa", "Baixa", "Baixa", "Baixa",
"Baixa", "Baixa", "Mediana", "Mediana", "Mediana",
"Mediana", "Mediana", "Mediana", "Mediana", "Mediana",
"Mediana", "Mediana", "Mediana", "Mediana", "Mediana",
"Mediana", "Mediana", "Mediana", "Mediana", "Mediana",
"Mediana", "Mediana", "Mediana", "Mediana", "Mediana",
"Mediana", "Mediana", "Mediana", "Mediana", "Mediana",
"Mediana", "Mediana", "Mediana", "Mediana", "Mediana",
"Alta", "Alta", "Alta", "Alta", "Alta", "Alta", "Alta",
"Alta", "Alta", "Alta")
# Cruzando Estatura com Sexo
############################
tab <- table(Estatura,Sexo)
tab
+--------------+
|
Sexo
|
+----------+------+-------+
| Estatura | Fem | Masc |
+----------+------+-------+
| Baixa
|
11 |
1 |
| Mediana |
14 |
19 |
| Alta
|
0 |
10 |
+----------+------+-------+
> chisq.test(tab)
# Cálculo do X2
Pearson's Chi-squared test
data: tab
X-squared = 18.792, df = 2, p-value = 8.307e-05
Warning message:
In chisq.test(tab) : Chi-squared appraximation may be
incorrect
Novamente, devido à restrições quanto a configuração da
tabela, a análise pelo quiquadro (X2) não é válida (ver
advertência, ou Warning message).
Também aqui, podemos observar pelo gráfico de colunas uma
forte evidência de associação, indicando que o sexo feminino
apresenta as menores estaturas enquanto que o sexo masculino as
maiores.
require(vcd)
# carregando o pacote vcd
assocstats(tab) # commando para as medidas de associação
X^2 df
P(> X^2)
Likelihaad Ratia 23.920 2 6.3958e-06
Pearsan
18.792 2 8.3069e-05
Phi-Caefficient
: 0.585
Cantingency Caeff.: 0.505
Cramer's V
: 0.585
Apresentação dos cálculos:
i) Coeficiente de contingência: t = min(3, 2) = 2
C
18.792

18.792  55
C*  0.505 
18.792

73.792
0.2547  0.505
2
 0.718
(2  1)
ii) Coeficiente V de Cramér:
V
18.792

(2  1)  55
18.792

55
0.3417  0.585
Como podemos observar pelos valores de C, C* e V-Cramér, a
associação entre Sexo e Estatura é forte.
Desta forma, temos forte evidência de que as alunas de
Estatística 1, turma 2015, são mais baixas do que os alunos 10cm,
em média.