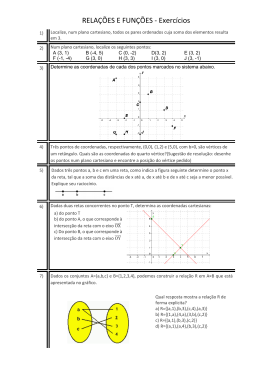
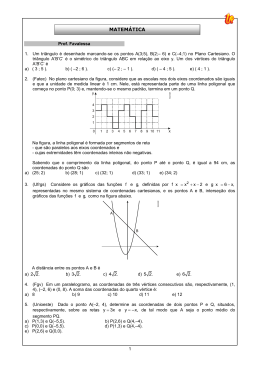
CEEJA “MAX DADÁ GALLIZZI”
PRAIA GRANDE - SP
BIBLIOGRAFIA
Os textos e os exercícios foram retirados e/ ou pesquisados nos
seguintes livros:
MATEMÁTICA
DANTE, Luiz Roberto. Tudo é Matemática. São Paulo: Ática,
2002. (5a a 8a séries)
DI PIERRO NETTO, Scipione. Matemática Conceitos e
Histórias. São Paulo: Scipione, 1998. ( 5a a 8a séries)
GIOVANI, José Rui. Et all. A Conquista da Matemática. São
Paulo: FTD, 1998. (5a a 8a séries).
13
MORI, Iracema. ONAGA, Dulce Satiko. Matemática Idéias e
Desafios. São Paulo: Saraiva, 1996. (5a a 8a séries)
LEIA COM ATENÇÃO!!!
A matemática é uma das mais importantes ferramentas
da sociedade moderna. Apropriar-se dos conceitos e
procedimentos matemáticos básicos contribui para a
formação do cidadão engajando-o no mundo do
trabalho, das relações sociais, culturais e políticas.
Para exercer plenamente a cidadania, é preciso saber
contar, comparar, medir, calcular, resolver problemas,
construir estratégias, comprovar e justificar resultados,
argumentar logicamente, conhecer formas geométricas,
organizar, analisar e interpretar criticamente as
informações, conhecer formas diferenciadas de abordar
problemas.
Nesta U.E. abordaremos o uso dos números associados
à reta numérica e ao plano, formando o sistema
chamado de Plano Cartesiano, que nos possibilita
localizar objetos, pontos, pessoas, países. Conforme a
área de interesse onde estiver inserido.
Resolva os exercícios no caderno e não nesta apostila.
Estes exercícios servirão de apoio para o Ensino
Médio, que, com certeza, você seguirá conosco.
Procure-nos assim que surgirem as primeiras dúvidas
estamos aqui para ajuda-lo a superar os desafios.
COORDENADAS E PLANO CARTESIANO
Coordenadas são informações que nos são fornecidas, em
alguma situação, para localização de objetos, pessoas ou pontos.
Essas informações podem vir em diversas formas, como por
exemplo: endereços, CEP’s, em geral com a associação de
números.
Geograficamente as coordenadas são apresentadas pela
associação de números com círculos imaginários chamados
meridianos e paralelos.
Cotidianamente as coordenadas são usadas em guias (mapas) de
cidades associando-se nomes com números, ou seja, os
endereços.
Basicamente necessitamos de 2 informações para localizarmos
um determinado ponto ou objeto.
Para facilitar essa localização, em matemática, utilizamos o
Plano Cartesiano.
Num jogo de xadrez, você pode indicar a localização de uma
peça por um código que indique a coluna e a linha da casa onde
ela está; e é por isso que muitas partidas de campeonatos
internacionais de xadrez podem ser disputadas à distância.
Plano Cartesiano é aquele que contém duas retas numeradas
(retas reais) que se cruzam no ponto zero das duas, formando
um ângulo de 90o, como veremos a seguir.
Pontos no plano:
Quando precisamos localizar pontos sobre um plano, que
pode ser um mapa ou um gráfico, utilizamos duas retas
numeradas que tenham a mesma origem e formem um ângulo
reto. Essas retas são denominadas eixos, e a unidade de medida
utilizada para marcar os números inteiros é a mesma para os
dois eixos.
Veja:
Simplificando nosso trabalho damos nomes a essas duas retas. A
horizontal é a X (abscissa), a vertical é a Y (ordenada).
Reta numerada
- 01 -
- 02 -
Quando caminhamos sobre o eixo horizontal, partindo do zero
para a direita, encontramos os números positivos. E quando, ao
contrário, partimos do zero para a esquerda, encontramos os
números negativos.
Sobre o eixo vertical, partindo da origem (zero) para cima,
encontramos os números positivos; para baixo, os números
negativos.
No eixo vertical, também chamado eixo das ordenadas,
para cima da origem marcamos os números positivo e, para
baixo, os números negativos.
As coordenadas são indicadas por um par ordenado de
números: o primeiro é a abscissa e o segundo é a ordenada,
sempre partindo da origem.
Você seria capaz de localizar os pontos colocados nesse plano
(desenho abaixo)?
Resumindo:
Localizar um ponto no plano é determinar suas
coordenadas. Para isso, usamos dois eixos perpendiculares com
a mesma origem e a mesma unidade de medida de comprimento.
No eixo horizontal, também chamado eixos das
abscissas, para a direita da origem estão os números
positivos e, para a esquerda, os números negativos.
Você não deve ter conseguido escrever uma localização para os
pontos dados pois não havia informações suficientes para isso.
Por isso associamos os números a essas duas retas.
Esses números têm o nome de coordenadas. As coordenadas
são sempre associadas a um plano cartesiano. As coordenadas
têm uma organização própria: em primeiro lugar o número
localizado na reta x e depois, separado por vírgula, o número
localizado na reta y.
- 03 - 04 -
Exemplos de pares ordenados:
reta x
reta y
Exemplo 2
reta x
reta y
A
(3,8)
(4,1)
B
Exemplo 1:
Os pontos A e B estão localizados no Plano Cartesiano, suas
coordenadas podem ser dadas olhando-se as linhas tracejadas e
contando os pontos onde cortam cada reta. Lembrando que a
horizontal é x e esse é o número que deve aparecer em 1o lugar.
Assim as coordenadas do ponto A são: 2 na reta x e 4 na reta y,
escrevemos (2,4); as coordenadas do ponto B são –2 na reta x e
2 na reta y, escrevemos (-2,2).
Para localizarmos determinado ponto no plano, localizamos o 1º
número (da reta x) e traçamos uma reta por ele. Depois,
localizamos o 2o número (da reta y) e traçamos outra reta. Onde
as duas retas se encontram é a localização do ponto que
procuramos.
- 05 –
Outro uso do sistema de Coordenadas é em geografia na
localização de ruas cidades país e outro ponto de interesse em
um mapa.
A posição geográfica de uma cidade em um mapa é obtida
tomando-se como referência a linha do equador e o meridiano
de Greenwich.
Equador
- 06 -
a) poltrona A
b) poltrona B
Exercício 1:
4
3
2
1
c) poltrona C
d) poltrona D
D
A
B
1
2
3
C
4
5
6
PALCO
Exercício 3:
Em cidades planejadas é mais fácil localizar um ponto qualquer.
Vamos supor que o mapa abaixo represente o centro de uma
cidade planejada. Três amigos, Ana, Beto e Carlos, combinaram
de se encontrar no centro da praça XV de Novembro. Ana está
na esquina indicada pela letra A, Beto na esquina indicada pela
letra B e Carlos na esquina indicada pela letra C.
Tomando como referência o centro da praça, como podemos
localizar cada amigo.
Dica: use esquerda e direita; acima e abaixo. Sempre tendo
como referência a praça.
A)
Exercício 2:
Em um auditório as poltronas estão dispostas em 6 colunas e 4
linhas, conforme mostra o desenho abaixo. Sabendo que o
primeiro número do par indica a coluna e o segundo número
indica a linha, escreva o par ordenado que corresponde a:
- 07 –
Observe a localização da torre da igreja na maquete. Esta
localização pode ser representada pelo par ordenado (B,7).
Dê a localização do:
a)restaurante
B)
b) chafariz
c)menino de bicicleta
O que você encontra em:
a) (L,5)
b) (B,4)
- 08 -
c) (E,2)
Exercício 4:
Em seu caderno, ou peça uma folha de papel quadriculado ao
professor, desenhe as retas numeradas e localize os seguintes
pontos, conforme as coordenadas dadas:
a) A (3,2)
f) F (-1,5)
b) B (1,5)
g) G (5,-1)
c) C (5,2)
h) H (4,-3)
d) D (-3,1)
i) I (2,3)
e) E (-4,4)
j) J (4 3)
X
-2
-1
0
1
2
3
4
Y
7
6
5
4
3
2
1
Vemos que com esta tabela organizamos pares
ordenados, ou seja, todas equações podem ser
representadas em um Plano Cartesiano.
Chamamos essa representação de resposta
gráfica ou geométrica dessa equação.
No caso das equações de 1o grau podemos observar que os
pontos ficam alinhados, formando uma linha reta. Observe o
modelo:
SISTEMAS DE EQUAÇÕES DO 1O GRAU
Vamos considerar a equação x + y = 5, o que esta equação quer
dizer?
A resposta seria: quais os números que somados têm como
resultado o número 5?
Existem infinitos números, mas alguns exemplos são:
-2 + 7 = 5
-1 + 6 = 5
0+5=5
1+4=5
2+3=5
3+2=5
4+1=5
5+0=5
6–1=5
7–2=5
Estas equações são chamadas de Equações do 1o grau pois não
temos nenhuma “letra” com uma potência diferente de 1.
Podemos colocar esses números em forma de tabela:
Vimos que uma equação pode ser representada num Plano
Cartesiano. Agora veremos outra forma de resolver essas
equações. Obteremos os resultados algebricamente, ou seja,
através de operações matemáticas.
As equações nos ajudam a descobrir respostas para situações
cotidianas, como por exemplo:
- 09 –
- 10 -
Exemplo 1:
Exemplo 2:
Situações que podem ser resolvidas com o
auxílio de sistema.
A soma entre dois números é 26 e a diferença entre eles é 4.
Quais são esses números?
Digamos que x e y sejam os números procurados, teremos as
seguintes equações:
 x  y  26

x  y  4
Esta é a representação equacionada do
Podemos elaborar o seguinte sistema
problema.
Vejamos como encontrar os números que são solução do
problema.
O método mais utilizado é o da ADIÇÃO.
Somaremos as duas equações ordenadamente, ou seja, x com x,
y com y e número com número.
 x  y  26
+

x  y  4
2x
= 30
x=
30
2
x = 15
Antônio e Carlos ganham juntos R$ 1 500,00. Sabendo que
Antônio ganha R$ 300,00 a mais que Carlos, quanto ganha cada
um?
No lugar
do x colocamos o valor
encontrado, ou seja , 15. Escolhendo uma
das equações do sistema.
Assim temos: x + y = 26
15 + y = 26
y = 26 - 15
y = 11
Encontrando o valor de y que é 11.
- 11 -
 A  C  1500

 A  C  300
Resolvendo o sistema pelo método da adição:
 A  C  1500
+

A

C

300

2A
= 1 800
A=
1800
2
Substituindo o valor de A em
qualquer das equações, temos:
A + C = 1500
900 + C = 1500
C = 1500 - 900
A = 900
C = 600
Resposta: Antonio ganha R$ 900,00 e Carlos ganha R$ 600,00.
- 12 -
Exemplo 3 :
Exercício 05:
Observe os pontos situados no quadriculado da figura onde estão
indicados os eixos horizontal e vertical:
Mais um tipo de sistema para ser resolvido pelo método da
adição:
Quais são as coordenadas dos sete pontos: E, F, G, H, I, J e K?
 x  3 y  1

5 x  3 y  17
 x  3 y  1
+

5
x

3
y

17

4x
= 16
16
x=
4
No lugar do x colocamos o valor
encontrado, ou seja , 15. Escolhendo
uma das equações do sistema.
Assim temos: -x - 3 y = - 1
- 4 - 3 y = -1
- 3y = - 1 + 4
-3 y = 3
x= 4
y=
3
3
y = -1
Encontrando o valor de y que é -1.
- 13 –
Exercício 06:
Desenhe um quadriculado e assinale os pontos:
A
B
C
D
E
(a; 1)
(2; 2)
(2; 0)
(0; 4)
(5; - 2)
F (- 3; - 4)
G (0; - 5)
H (- 1; 0)
I (- 4; - 3)
J (5; - 4)
- 14 -
Exercício 7
SITUAÇÕES QUE ENVOLVEM SISTEMAS
Resolva os sistemas:
a)
x  y  1

x  y  9
Exercício 8
f)
 x  y  14
b) 
x  y  6
g)
 x  y  23

 x  y  59
h)
c)
3x  y  8

7 x  y  42
A soma de dois números é 40 e a sua diferença é 32. Quais são
esses números?
3x  2 y  10

5 x  2 y  22
A soma de dois números é 15 e a diferença entre eles é 3. Quais
são esses números?
 a  2b  7

a  3b  9
Exercício 9
Exercício 10
A diferença de dois números é 4 e a soma desses números é 20.
Quais são esses números?
 x  y  20
d) 
 x  y  10
a  3b  5
i) 
2a  3b  8
Exercício 11
x  y  8

x  y  2
 x  3 y  1
j) 
5 x  3 y  17
Exercício 12
e)
A soma de dois números é 45. O maior tem 5 unidades a mais
que o menor. Quais são esses números?
Um comerciante comprou 70
canetas e 100 lápis por R$
325,00. Uma caneta e um lápis juntos custam R$ 4,00. Quanto
custa cada lápis e cada caneta?
Exercício 13
Numa granja, entre galinhas e coelhos, existem 175 cabeças e
500 patas. Quantas são as galinhas e quantos são os coelhos?
- 15 -
- 16 -
Exercício 14
Exercício 04
Em um estacionamento havia carros e motocicletas num total de
43 veículos e 150 rodas. Calcule o número de carros e de
motocicletas estacionados.
 Consulte o professor
Exercício 05
E (4,2)
F (1,5)
G (-2,3)
H (-4, 1)
I (-3,-3)
J (1,-3)
K (1,-1)
GABARITO
Exercício 06
 Consulte o professor
Exercício 01
Exercício 07
A – 4 direita e 2 para cima
C – 1 direita e 2 para baixo
B – 5 esquerda e 3 para baixo
Exercício 02
a)5ª coluna e 3ª linha
b)3ª coluna e 2ª linha
c) 4ª coluna e 1ª linha
d) 1ª coluna e 3ª linha
Exercício 03
a) (5,4)
b) (10,4)
c) (41,18)
d) (15,5)
e) (5,3)
f) (5,7)
g) (4,1)
h) (-3,2)
i) (-1,2)
j) (4,-1)
Exercício 08
Resp.: 36 e 4
A – a) (F,8)
b) (F, 5)
B – a) açougue
b) Posto de Gasolina
- 17 -
c) ( G,7)
c) Estátua
Exercício 09
Resp.: 9 e 6
- 18 -
Exercício 10
Resp.: 12 e 8
Exercício 11
Resp.: 25 e 20
Exercício 12
Resp.: Caneta R$ 2,50 e Lápis R$ 1,50
Exercício 13
Resp.: 100 galinhas e 75 coelhos
Exercício 14
Resp.: 32 carros e 11 motos
- 19 -