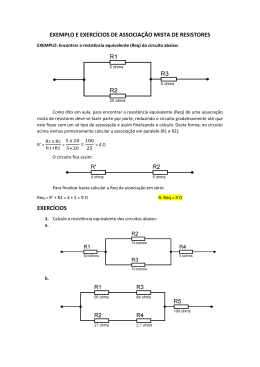
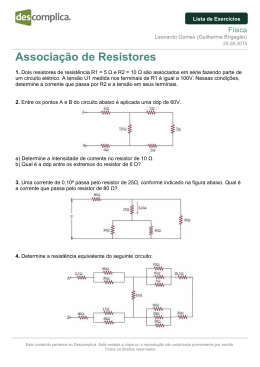
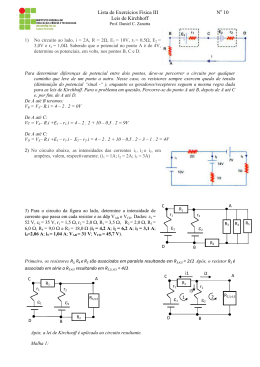
Prof. Fernando Buglia
Exercícios – Associação de resistores
1. (Cesgranrio) Um resistor A tem o valor de sua resistência expresso por 1 – x, enquanto um outro resistor B tem o
valor de sua resistência expresso por 1 + x, com 0 < x < 1. R1 e R2 são, respectivamente, as resistências
equivalentes obtidas quando A e B são associados em série e em paralelo. As expressões que representam R 1 e R2,
nessa ordem, são
a) 1  x2 e
b) 1  x2 e
c) 2 e 1 – x
d) 2 e
e) 2 e
1  x2
2
2
1  x2
2
1  x2
2
2
1  x2
2. (Ufrgs) Considere o circuito abaixo.
Neste circuito, todos os resistores são idênticos, e C1 e C2 são dois interruptores que podem estar abertos ou
fechados, de acordo com os esquemas numerados a seguir.
C1 C2
aberto
fechado X
(1)
X
C1 C2
aberto
X
fechado
(2)
X
C1 C2
aberto
X
fechado
(3)
X
C1 C2
aberto
fechado X
(4)
X
Assinale a alternativa que apresenta corretamente o ordenamento dos esquemas de ligação, em ordem crescente da
corrente elétrica que passa no resistor R 4 .
Página 1 de 4
Prof. Fernando Buglia
a) (4) – (2) – (3) – (1)
b) (1) – (3) – (2) – (4)
c) (2) – (4) – (3) – (1)
d) (2) – (3) – (4) – (1)
e) (3) – (2) – (1) – (4)
3. (Epcar (Afa)) O esquema abaixo mostra uma rede elétrica constituída de dois fios fase e um neutro, alimentando
cinco resistores ôhmicos.
Se o fio neutro se romper no ponto A, a potência dissipada irá aumentar apenas no(s) resistor(es)
a) R1 e R3
b) R2 e R5
c) R3
d) R 4
Página 2 de 4
Prof. Fernando Buglia
Gabarito:
Resposta da questão 1:
[D]
R1  RA  RB  1  x  1  x  2
R2 
RA.RB
(1  x)(1  x) 1  x 2
.


RA  RB 1  x  1  x
2
Resposta da questão 2:
[C]
A corrente em R4 será maior quando a resistência do restante do circuito for menor.
R
.
2
(2) R2 ligada R3 desligada  (Req )2  (R1  R2 )  2R .
(1) R2 em curto, R3 ligada  (Req )1  (R1 / /R3 ) 
(3) As duas ligadas  (Req )3  (R1  R2 ) / /R3 
(4) As duas desligadas  (Req )4  R1  R .
2RxR 2R
.

2R  R
3
A ordem crescente de corrente será a ordem decrescente de resistência. Portanto, (2), (4), (3) e (1).
Resposta da questão 3:
[C]
Quando o fio neutro se rompe, alteram-se as tensões apenas nos resistores R3 e R4. No circuito original a tensão em
cada um deles é U1 = 110 V.
Calculemos, então, as respectivas potências (P3 e P4) dissipadas nesses dois resistores nessa situação original.

U12 1102
P


 3
R3
220


2
2
P  U1  110
 4 R
110
4

 P3  55 W.
 P4  110 W.
Com o fio neutro rompido, esses dois resistores ficam associados em série e a associação submetida à tensão U =
220 V e percorridos pela mesma corrente (i), como mostra a figura a seguir.
Para calcular as novas potências ( P3' e P4' ) nesses resistores, precisamos primeiramente calcular as novas tensões a
que eles ficam submetidos (U3 e U4), respectivamente.
U3  U4  U
 U3  U4  220 V.
I
Página 3 de 4
Prof. Fernando Buglia
Mas:

U3  R3 i  U3  220 i


U4  R4 i  U4  110 i

U3 220 i

 2  U3  2 U4 . (II)
U4 110 i
Substituindo (II) em (I):
2U4  U4  220  U4 
220
V.
3
Voltando em II:
440
 220 
U3  2 
 U3 
V.

3
 3 
Assim:

  440 


2
3
U
P'  3  
3

R3
220


  220 


2
3
P4'  U4  

R4
110
2


  880
3
 P3'  293 W.
2


  440
3
 P4'  49 W.
Comparando as duas situações:
P3'  P3 e P4'  P4 .
Portanto, a potência dissipada aumenta apenas no resistor R3.
Página 4 de 4