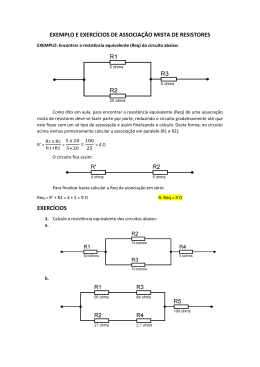
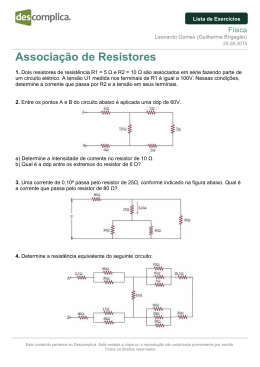
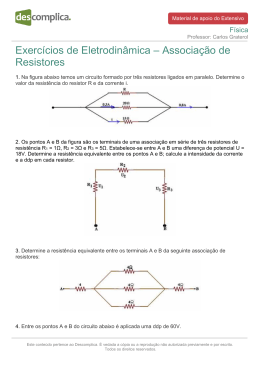
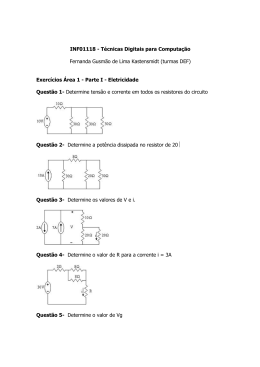
No 10
Lista de Exercícios Física III
Leis de Kirchhoff
Prof. Daniel C. Zanotta
No circuito ao lado, i = 2A, R = 2Ω, E1 = 10V, r1 = 0,5Ω, E2 =
3,0V e r2 = 1,0Ω. Sabendo que o potencial no ponto A é de 4V,
determine os potenciais, em volts, nos pontos B, C e D.
1)
Para determinar diferenças de potencial entre dois pontos, deve-se percorrer o circuito por qualquer
caminho que leve de um ponto a outro. Nesse caso, os resistores sempre exercem queda de tensão
(diminuição do potencial “sinal -“ ), enquanto os geradores/receptores seguem a mesma regra dada
para as leis de Kirchhoff. Para o problema em questão, Percorre-se do ponto A até B, depois de A até C
e, por fim, de A até D.
De A até B teremos:
VB = VA– R.i = 4 – 2 . 2 = 0V
De A até C:
Vc = VA– R.i +E1 – r1.i = 4 – 2 . 2 + 10 – 0,5 . 2 = 9V
De A até C:
VD = VA– R.i +E1 – r1.i - E2 – r2.i = 4 – 2 . 2 + 10 – 0,5 . 2 – 3 – 1 . 2 = 4V
2) No circuito abaixo, as intensidades das correntes i1, i2 e i3, em
ampères, valem, respectivamente. (i1 = 1A; i2 = 2A; i3 = 3A)
C
3) Para o circuito da figura ao lado, determine a intensidade de
corrente que passa em cada resistor e as ddp VAB e VCD. Dados: 1 =
52 V, 2 = 35 V, r1 = 1,5 , r2 = 2,0 , R1 = 3,5 , R2 = 2,0 , R3 =
6,0 , R4 = 9,0  e R5 = 18,0  (i1 = 4,2 A; i2 = 6,2 A; i3 = 3,1 A;
i4=2,06 A; i5 = 1,04 A; VAB = 31 V; VCD = 45,7 V).
A
R1
r1
r2
1
D
R3
2
R4
R2
B
Primeiro, os resistores R3, R4 e R5 são associados em paralelo resultando em R3,4,5 = 2. Após, o resistor R5 é
associado em série a R3,4,5 resultando em R2,3,,4,5 = 4.
i1
i2
A
C
A
C
R1
R1
r1
r2
r1
r2
i3
R2,3,4,5
2
1
R
1
D
B
R2
Após, a lei de Kirchooff é aplicada ao circuito resultante.
Malha 1:
1
3,4,5
2
D
2
B
R5
Partindo de D: + E2 – r2 . i3 +r1 . i1 – E1 = 0
35 – 2 . i3 +1,5 . i1 – 52 = 0
Malha 2:
Partindo de B: - R2345 . i2 +r2 . i3 – E2 = 0
- 4. i2 + 2 . i3 – 35 = 0
Lei dos nós:
i1 + i2 = i3
A corrente que passa em R1 é i1. A corrente que passa em R2 é i2. Aa corrente que passa em R3,4,5 é i2
também. Nota-se que este resistor é resultante de uma associação em paralelo. Para saber quanto vale a
corrente que passa individualmente em cada um, é necessário saber qual é a d.d.p V3,4,5 em R3,4,5, que
é a mesma que cada um dos resistores R3, R4 e R5. Após, deve-se aplicar V = R . i para cada um deles
com a tensão V3,4,5 para encontrar iR3, iR4, iR5.
4) Determine o valor de R para que i seja igual a 3 A. Dados: 1 = 85 V, 2 = 25 V, r1 = 2  e r2 = 1  (10
).
r1
1
2
r2
11

i
9
A
10 
B
R
Para resolver este problema é necessário saber qual é a tensão que chega nos terminais A e B. Para
tanto, basta partir de um dos pontos que formam a ligação em paralelo de resistores (A ou B) e chegar no
outro. Saindo de A:
(Como fizemos em 1)
VB = VA -11.i +E1-r1 . i – r2 . i – E2
VB – VA = -11.i +E1-r1 . i – r2 . i – E2 = 18V
Com VBA = 18V aplicada na associação de resistores, tem-se para o Req a essa associação:
VBA = Req . i
18 = Req . 3
Req = 6
E o resistor equivalente:
1 / Req = 1 / 9 + 1/ (10+R)
R = 10 
1 / 6 = 1 / 9 + 1/ (10+R)
5) No circuito indicado, determine i, R e  (4 A; 10 ; 52 V). 4 
6A
10 A
i
2

R
100 V
6)
Para o circuito da figura ao lado, as baterias têm fem 1 =
4 V e 2 = 2 V, e ambas têm resistência interna r1 = r2 = 1
. a) Para que valor devemos ajustar o reostato R para que
a lâmpada L não acenda ? (1 ); b) Com a lâmpada L
apagada, qual o valor da corrente que passa por R ? (2 A).
r1
r2
R
2
L
1
7) No circuito, quando o cursor é colocado no ponto C, o
amperímetro A não acusa passagem de corrente. a) Qual a
ddp entre os pontos C e B ? (6 V); b) Se R vale 20 , qual
o valor da corrente que passa por ela ? (0,5 A); c) Qual o
valor da resistência entre B e C ? (12 ).
10 V
B
R
A
C
A
2
4V
50 
8)
No trecho do circuito ao lado, determine os valores
das correntes i3, i4, i5.
Formulário
R
 L
A
V  R.i
i
q
t
P  V .i
P
V2
R
Este documento está disponível online no endereço:
academico.riogrande.ifrs.edu.br/~daniel.zanotta