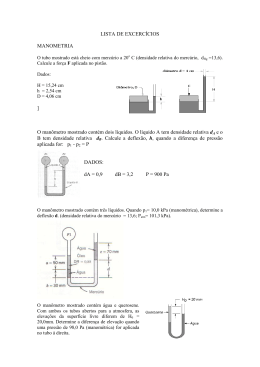
Capítulo 2 – Estática dos
Fluidos
ME4310 e MN5310
02/09/2009
Reflexões sobre o
que foi estudado
na aula anterior.
é uma grandeza escalar
pressão em um ponto
fluido pertecente a um
fluido
medidores de pressão
contínuo
incompressível
repouso
unidades de pressão
Pressão
01/09/2009 - v9
escalas de pressão
carga de pressão
teorema de Stevin
lei de Pascal
Exercício proposto na aula anterior
Sabendo-se que o esquema abaixo se encontra em equilíbrio em um
local onde a pressão barométrica é 700 mmHg, pede-se:
a) a pressão no fundo do recipiente na escala efetiva (pF);
b) a pressão pF na escala absoluta;
c) a cota x.
Equaçãomanométrica de (1) a pF
ado tando (1) com origem:
patm  5  H2O  1  r  padrão  1,5  H2O  pF
Trabalhando na escala efetiva:
0  5  10000  1  10  1000  9,8  1,5  10000  pF
pF  163000
N
m2
(ou Pa)  (a)
pFabs  pF  patmloc al
 700  101234
pFabs  163000  

760


N
pFabs  256241,8
(ou Pa)  (b)
m2
Equaçãomanométrica de (1) a (5) :
patm  5  H2O  1  r  padrão  1  H2O  xH2O  p5
0  50000  98000  10000  x10000 
x  13,79 m
50  4
  0,79792
Outro exemplo do capítulo 2 e que
caiu na prova em 03/10/2007
Primeira situação
p1  0,4    h  m  2  h    p2
1,9  1,36  105  0,4  800  10  h  110000  2  h  800  10  114000
258400  3200  h  110000  16000  8000  h  114000
131600  h  102000  h  1,29 m
Segunda situação
p1'  (0,4  x)    (h  2x)  m  2  h  x     p2
2,28  1,36  105  (0,4  x)  800  10  (h  2x)  110000  2  h  x   800  10  114000
310080  3200  8000x  1,29  110000  220000x  16000  8000  1,29  8000x  114000
51700  x  204000  x  0,253 m
resposta h  x  1,29  0,253  1,543 m
VAMOS NOS DETER MAIS NOS
MEDIDORES DE PRESSÃO.
MANÔMETROS DE TUBO RETO COM RESERVATÓRIO
O Projeto de um manômetro de coluna pode ser definido sob
diferentes formas com o objetivo de atender aos requisitos de
vários serviços. O manômetro de tubo reto com reservatório é
um destes casos.
O manômetro de tubo reto com reservatório difere do
manômetro de tubo em “U” por causa da relação entre as
áreas dos dois sendo que uma dela é muitas vezes maior do
que a outra. Como resultado deste aspecto construtivo, a
altura do líquido no reservatório muda pouco, enquanto que
no outro ramo a mudança é bastante sensível.
Vdesceu  Vsubiu
A1  h  A2  H
Manômetro metálico do tipo
Bourdon
pm  pint e rna  pe x te rna
pex terna
É comum se considerar:
pm como pressãoefetiva
Só escalapositiva  manômetro
Só escalanegativa  vacuômetro
Escalas positivas e negativas manovacuômetro
pmanométric
a  pm
pint erna
Exercício de prova que foi baseado no exercício 2.15 do
livro do professor Franco: no manômetro da figura são
indicados os níveis dos fluidos antes e depois de ser
ligado ao reservatório A. Qual a leitura em Pa do
manômetro metálico instalado em A. Dados: 1 =
10000 N/m³ e 2 = 9200 N/m³
Resolução
2
2
D2 h d2
h d
300  4 
h 
 
 h     

  1,5 mm
4
2
4
2 D
2
 40 
pgás  2  h  2  0,3  1  0,3  2  patm
Na escala efetiva :
pgás  0,3  9200  0,3  10000  2  0,0015  9200  267,6 Pa
pm  pint  pe x t  0  (267,6)  267,6 Pa
ATIVIDADE: FAZER O
EXERCÍCIO 2.14; 2.16 E
2.17 DO LIVRO DO
PROFESSOR FRANCO
BRUNETTI.