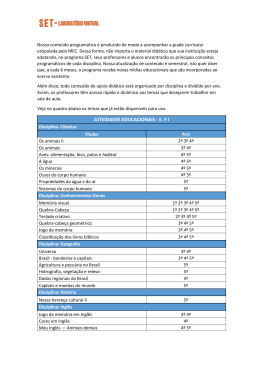
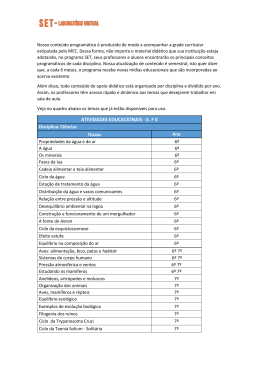
A TABUADA
Ernesto Rosa
− É preciso saber de cor a tabuada? − SIIIMM...
− É preciso ficar decorando a tabuada? − NÃÃÃÕO...!
Não é para se trancar em um quarto e ficar gritando: 6 vezes 1, 6; 6 vezes 2, 12; 6
vezes 3, 18... Da frente para trás, de trás para frente e salteado. O que é preciso é construir a
tabuada a partir de exercícios interessantes, o que, claro, levará à memorização. Mas não é
esse o objetivo.
Cada aluno segue um caminho próprio na construção da tabuada. O problema é dele e
não há como ajudá-lo com coisas prontas. A única coisa que o professor deve fazer é dizer:
4×6 é 6+6+6+6, quatro vezes. O resto é com o aluno! E ele começa a tabuada assim mesmo
com somas repetidas; depois, vai evoluindo. Um problema como “quantas rodas têm três
bicicletas?”, começa sendo resolvido assim: 2 + 2 + 2. Depois são criadas outras soluções.
Veja o caminho de um aluno, que pude acompanhar:
A tabuada do 2 foi fácil. O aluno bem cedo a construiu fazendo dobros. No cotidiano
há muitos pares, duplas e casais. Trabalhou simetrias, jogou par ou ímpar, formando os pares.
Aprendeu a contar de 2 em 2 e o conceito de números pares e ímpares. Assim, aprendeu a
dobrar um número.
A do 3 foi um pouco mais difícil, mas o próprio ambiente forneceu o que ele
precisava: trios e ternos; no relógio, as horas 3, 6, 9 e 12 ocupam lugar de destaque; a noção
de dúzia e meia dúzia ajudou um pouco. Essas coisas, juntas com muitas outras, levaram-no à
contagem de 3 em 3 e, em seguida, a formar os triplos.
A tabuada do 4 foi feita com o dobro do dobro, aliado a outras noções: 4×7 é o dobro
de 7, 14, e o dobro de 14, 28. Cada vez mais rápido, até ir diretamente ao 28. 4×9, 18, 36.
A comutatividade já estava sendo usada calculando, por exemplo, 7×3 como 3×7.
A tabuada do 5 me pareceu ter sido construída assim:
1º momento: 5×6 = 6+6+6+6+6 = 30.
Portanto, usou as somas repetidas, fazendo as contas como podia, às vezes, nos dedos
ou com palitinhos.
2° momento: Passou a inverter, porque é mais simples somar 5: 5×6 = 6×5 =
5+5+5+5+5+5, e, logo, passou a contar de 5 em 5: 6×5 = 5, 10, 15, 20, 25, 30. Isso envolve
os múltiplos de 5, ficando claro que terminam em 0 ou 5, já construindo a divisibilidade por 5.
3º momento: Usando a propriedade associativa, transformava pares de 5 em dezenas:
6×5 = (5+5) + (5+5) + (5+5) = 10+10+10 = 30.
4º momento: Usou que, formando pares de 5, ficava com a metade das parcelas:
6×5 = 10+10+10 = 3×10 = 30. Isso ele já sabia da tabuada do 2.
5º momento: Continuou com as abstrações reflexivas, passando a fazer:
1
6×5 = 3... 30, 8×5 = 4... 40. 7×5, como o 7 é ímpar, fazia 6×5 + 5 = 30+5 = 35.
Isso se associava a outro método: 7×5 é a metade de 7×10.
6º momento: As abstrações levaram a resultados mais interiorizados: 6×5 = 30, 8×5 =
40 etc.
Essa construção interagia com o olhar horas: se o ponteiro grande está no 4, são 20
minutos (4×5) etc. Saber ver horas em relógio de ponteiros, implica a tabuada do 5. Assim,
cada vez que acomodava uma nova maneira de fazer, passava a construir outra.
A tabuada do 6 foi construída com o dobro do triplo:
No primeiro momento, fazia 6×7 = 7+7+7+7+7+7.
Num segundo momento, depois de tentar 14 três vezes, passou a 21 duas vezes:
6×7, 21, 42 (3×7 e 2×21). Do mesmo modo: 6×4, 12, 24 (3×4 e 2×12) etc.
Esse modo de pensar interagia com as noções de dúzia e meia dúzia: 6×8 são 8 meias
dúzias, que valem 4 dúzias, e 4 dúzias são 48. Muitas informações se combinam fechando a
construção da tabuada. E é emocionante acompanhar essa demonstração da pujança humana.
São as compensações da sala de aula. É bonito ver um criança, com atrevimento, fazer: 6×7,
21, 42.
A tabuada do 9 foi relativamente fácil, usando o 10−1. Assim: 9 vezes 7 era 10 vezes 7
menos 1 vez 7, que era 70−7 ou 63. O que ele fazia de cabeça pode ser escrito assim: 9×7 =
(10−1)×7 = 10×7 − 1×7 = 70−7 = 63. Essa escrita, mostra quantas propriedades estão sendo
usadas e como a cabeça está sendo bem estruturada... por ela mesma. Mais tarde, ele deverá
escrever essas propriedades, caminhando para a Álgebra.
Para terminar, as tabuadas do 7 e do 8 foram mais difíceis, porém, de 7×1 até 7×6, ele
construiu com a comutatividade. O mesmo se deu com o 8, restando apenas 7×7, 7×8 e 8×8.
Às vezes, com o 8, tentava o dobro do dobro do dobro: 8×7... 14, 28, 56 ou então fazendo 8×7
como o dobro de 4×7, ou então com a distributividade: 8×7 = 8×5 + 8×2 = 40 + 16. O
trabalho com números quadrados levava a 7×7 e 8×8. Esse final foi mais difícil de passar ao
resultado decorado. Passou por um momento em que ele sabia os resultados: 56, 49, 64, mas
não sabia de quais eram e, então usava os métodos que construíra.
Multiplicar é formar múltiplos, exatamente isso. 4 vezes a parcela 6, é 6+6+6+6, é o
quarto múltiplo positivo de 6. O que queremos do aluno não é a tabuada, mas a formação de
múltiplos de 2 em 2, de 3 em 3, dobro do triplo, comutatividade, distributividade,
associatividade e outros componentes da estrutura dos números. O mais interessante é que
muitas dessas propriedades são construídas por todas as pessoas, mesmo as que não passaram
pela escola. Essas propriedades são necessárias no cotidiano. A escola deve apenas oferecer
oportunidades para o aluno verbalizá-las, escrevê-las e estruturá-las, caminhando para o
formal.
É muito empobrecedor apenas decorar os resultados! Apenas resultados a calculadora
faz melhor. Decorar resultados impede a criação, por isso, quanto mais o aluno ganha em
informação mais perde em ousadia, arrojo, atrevimento intelectual.
2
As contas não são mais necessárias, depois do advento das calculadoras. O que
permanece importante são as estruturas, que levarão diretamente à Álgebra. Sem as
propriedades das operações aritméticas o aluno não estará com base para a Álgebra.
7×5
35
35
35
Ver o site:
www.matinterativa.com.br
3