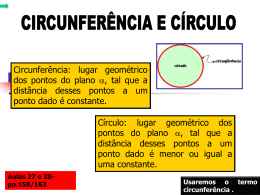
LUGARES GEOMÉTRICOS
3.º Ciclo do Ensino Básico
8.º ANO
Lugares Geométricos

Um lugar geométrico é uma região do
plano ou do espaço com determinadas
propriedades comuns.
O objectivo desta unidade é o estudo mais aprofundado
de alguns lugares geométricos de que já ouviste falar.
2
Circunferência e círculo
Um jardineiro quer construir um canteiro com a forma
de uma circunferência. Para isso coloca uma estaca
num ponto do terreno e prende nela uma corda. Na
outra ponta da corda coloca um objecto e vai fazendo,
com a corda totalmente esticada, um sulco no chão.
O jardineiro está a desenhar uma
circunferência sobre o chão. Todos
os pontos estão situados à mesma
distância do ponto onde se encontra
espetada a estaca (o centro da
circunferência).
3
Circunferência e círculo
Uma circunferência é o lugar geométrico dos pontos
do plano que são equidistantes de um ponto fixo
chamado centro da circunferência.
À distância de qualquer
ponto da circunferência ao
seu centro dá-se o nome de
raio da circunferência.
Na figura, o raio da
circunferência corresponde
ao
comprimento
do
segmento de recta [PC].
4
Circunferência e círculo
Os pontos A e B da figura abaixo estão situados no
interior da circunferência. A distância destes pontos ao
centro da circunferência é menor do que o raio.
Um círculo é formado por todos os pontos interiores à
circunferência e pela circunferência.
Assim, o círculo é o lugar
geométrico
dos
pontos
pertencentes
a
uma
circunferência ou ao seu
interior.
5
Circunferência e círculo
Na figura abaixo estão representados os pontos D e E.
A distância destes pontos ao centro da circunferência é
maior do que o raio da circunferência. Os pontos D e E
são pontos exteriores à circunferência.
O exterior de uma
circunferência é o lugar
geométrico dos pontos do
plano que distam do centro
da circunferência mais do
que o seu raio.
6
Circunferência e círculo
Considerando duas circunferências concêntricas (com o
mesmo centro) e raios diferentes, podemos definir um
lugar geométrico do plano situado entre as duas
circunferências. Essa região do plano designa-se por
coroa circular.
A
região
assinalada
a
amarelo
representa uma coroa circular. Os seus
pontos encontram-se a uma distância
do ponto C igual ou maior do que BC e
igual ou menor do que AC.
7
Mediatriz de um segmento de recta
Exemplo 1:
• Pretende-se construir uma
igualmente de duas localidades.
estrada
que
diste
A estrada vai ter de
corresponder à mediatriz do
segmento de recta que une
as duas localidades.
Desta forma, qualquer ponto
da estrada é equidistante
das duas localidades.
8
Mediatriz de um segmento de recta
9
Mediatriz de um segmento de recta
Propriedades:
• Um ponto qualquer da mediatriz de um segmento de
recta é equidistante dos extremos desse segmento.
• O ponto médio do segmento de recta é o ponto da
mediatriz desse segmento que se encontra à menor
distância dos extremos desse segmento de recta.
10
Mediatriz de um segmento de recta
Exemplo 2:
• O Professor de Educação Física quer que o João se
coloque num lugar que seja equidistante de três
colegas, de acordo com o que mostra a figura. Em que
lugar se deve colocar o João?
O João deve ficar colocado
na posição indicada. O ponto
assinalado
chama-se
circuncentro do triângulo e
corresponde à intersecção
das mediatrizes dos lados
do triângulos (mediatrizes
dos lados do triângulo).
11
Bissectriz de um ângulo
Considerando a recta r e o ponto P, não
pertencente à recta, a menor distância
entre o ponto P e a recta r é dada pelo
comprimento do segmento de recta [PA],
perpendicular à recta r, no ponto A.
A bissectriz de um ângulo é
uma semi-recta que divide o
ângulo em outros dois
ângulos
geometricamente
iguais.
12
Bissectriz de um ângulo
Para
construires
a
bissectriz de um ângulo
começas por desenhar o
arco [AB], centrando o
compasso no ponto V
(vértice do ângulo).
De seguida, abres o compasso com raio igual ao comprimento do
segmento de recta [AB]. Centras o compasso em A e depois em B,
traçando os arcos que se encontram a verde. Esses arcos interceptam-se
num ponto.
Traçando a semi-recta que passa por esse ponto e pelo vértice do
ângulo, obténs a bissectriz do ângulo.
13
Bissectriz de um ângulo
Cada um dos pontos da
bissectriz de um ângulo é
equidistante dos lados do
ângulo.
Por exemplo:
AP = BP e
CQ = DQ
Podemos agora definir a bissectriz como o lugar geométrico dos pontos
do plano equidistantes dos lados de um ângulo.
14
Bissectriz de um ângulo
Exemplo:
Se pretendermos colocar
candeeiros entre duas ruas
de modo a que cada um
deles esteja a igual distãncia
de ambas as ruas, teremos
de determinar a bissectriz
do ângulo formado pelas
duas ruas (linha a amarelo).
Como a figura ilustra, os candeeiros deveriam ficar segundo a bissectriz
do ângulo cujos lados são representados pelas duas ruas A e B.
15
Lugares geométricos no espaço
Superfície esférica e esfera
O vidro do qual é feito o abat-jour do
candeeiro de tecto (a amarelo) pode
imaginar-se como sendo uma região do
espaço cujos pontos se encontram todos a
igual distância de um ponto central fixo.
Ao lugar geométrico dos pontos do espaço
equidistantes de um ponto fixo chamado
centro, dá-se o nome de superfície
esférica.
O abat-jour
esférica.
representa
uma
superfície
16
Lugares geométricos no espaço
Superfície esférica e esfera
Se considerares agora todos os pontos da
superfície esférica e todos aqueles que
lhe são interiores, tens um novo lugar
geométrico denominado esfera.
Assim, a esfera é o lugar geométrico de
todos os pontos do espaço que se
encontram a igual ou menor distância
de um ponto fixo chamado centro.
A distância do centro da esfera a um
qualquer ponto da superfície esférica,
chama-se raio da esfera.
17
Lugares geométricos no espaço
Plano mediador
Supõe que tens dois candeeiros no
chão da tua sala, como se
representa na figuar ao lado.
Pretendes saber quais são os
lugares
da
sala
que
estão
equidistantes dos dois candeeiros.
Considerando o segmento de recta
cujos extremos são as bases dos
dois candeeiros, os pontos do plano
representado
a
verde
são
equidistantes das bases.
18
Lugares geométricos no espaço
Plano mediador
O plano representado a verde
denomina-se Plano Mediador do
segmento de recta.
O plano mediador de um
segmento de recta é o lugar
geométrico dos pontos do espaço
equidistantes dos extremos do
segmento de recta.
O plano mediador é perpendicular
ao segmento de recta e contém o
ponto médio desse segmento de
recta.
19
Bom trabalho!
FIM
20