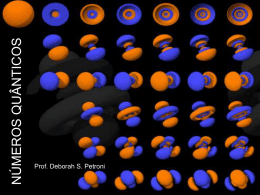
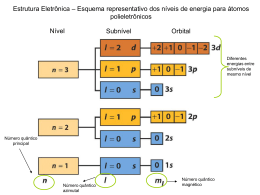
O Átomo e o Mundo Quântico
Surgimento da Mecânica Quântica: Século XX
Natureza ondulatória da Luz
Modelo de Bohr - 1913
Relacionou as idéias quânticas de Planck e Einstein e
explicou os espectros dos átomos excitados e acrescentou 3
postulados ao modelo atômico de Rutherford.
* O átomo é formado por
um núcleo e níveis de
energia quantizada, nos
quais os elétrons estão
distribuídos.
Surgimento da Mecânica Quântica
Natureza da Luz
(radiação eletromagnética)
Consiste de campos
elétricos e magnéticos
oscilantes
λ.ν = c
2 ciclos completos
3x108m/s (c-velocidade da luz).
Exercícios
1. Duas ondas eletromagnéticas são representadas abaixo:
(I)
(II)
(a) Qual a onda tem a maior freqüência?
(b) Se uma onda representa a luz visível e a outra, a radiação infravermelha,
qual é uma e qual é outra?
Resposta
(a) A onda (I) tem comprimento de onda mais longo (maior distância entre os
picos).
-
Quanto maior o comprimento de onda, menor a frequência (ν=c/λ).
Portanto a onda (I) tem frequência menor e a onda (II) tem
frequência maior.
(b) O espectro eletromagnético indica que a radiação IV tem
comprimento de onda mais longo do que a luz visível. Assim, a
onda (I) seria a radiação infravermelho.
Exercício
2. A Luz amarela emitida por uma lâmpada de vapor de sódio usada para
iluminação pública tem um comprimento de onda de 589 nm.
a) Qual é a freqüência dessa radiação (dados: velocidade da luz =
3x108m/s).
b) Quantos fótons de luz amarela são gerados pela lâmpada em 1 s?
Resposta
C = 3x108m/s).
ν=c/λ
ν= 3x108m/s /589 nm
Grandezas com unidades diferentes
Converter λ em namometro (nm) para metro (m)
ν= ((3x108m/s)/589 nm)(1nm/10-9m)
ν = 5,09 x 1014 s-1
Exercício
3. Calcule os comprimentos de onda (em nm) das luzes de trânsito. Suponha
que as frequências sejam: Verde (5,75 x 1014 Hz); amarelo (5,15 x 1014 Hz);
vermelho (4,27 x 1014 Hz).
Resposta
ν=c/λ
Verde (5,75 x 1014 Hz); amarelo (5,15 x 1014 Hz); vermelho (4,27 x 1014 Hz)
1Hz = 1s-1
C = 3x108m/s
Verde = 521 nm
Amarelo = 582 nm
Vermelho = 702 nm
Evolução da Teoria Atômica Quântica
Postulados de Planck:
A energia só pode ser liberada (ou absorvida) por átomos em certos
pedaços de tamanhos mínimos, chamados quantum.
A relação entre a energia e freqüência é dada por:
E = hν
onde h é a constante de Planck (6,626 x 10-34 J s).
E, de acordo com a teoria de Planck, a energia é sempre emitida e
absorvida pela matéria em múltiplos inteiros de hν, 2hν, 3hν e
assim sucessivamente.
Exemplo:
Se a quantidade de energia emitida por um átomo for 3hν, dizemos que foram
emitidos 3 quanta de energia.
E, que as energias permitidas são quantizadas, isto é, seus valores são restritos
a determinadas quantidades.
Quantização de energia
Para entender a quantização, considere a subida em uma rampa
versus a subida em uma escada:
na rampa, há uma alteração constante na altura (aumenta de
maneira uniforme e contínua).
enquanto na escada, há uma alteração gradual e quantizada na
altura.
Evolução da Teoria Atômica Quântica
O efeito fotoelétrico e fótons
O efeito fotoelétrico fornece evidências
para a natureza de partícula da luz “quantização”.
Einstein supôs que a luz trafega em pacotes de energia
denominados fótons.
A energia do fóton é dada por:
E = hν
Evidências do Comportamento Quântico do Átomo
Espectro da Luz Branca Emitida por um Filamento Aquecido
Espectro de um Tubo de descarga preenchido com Hidrogênio
Evidências do Comportamento Quântico do Átomo
Espectros de Emissão Atômica do H, Hg e Ne
Os elementos gasosos excitados emitem luz, cujos espectros são
únicos para aquele átomo (impressão digital do átomo).
Técnica poder ser usada para identificação de elementos.
Os Espectros Atômicos
• Balmer: descobriu que as linhas no espectro de linhas visíveis do
hidrogênio se encaixam em uma simples equação matemática.
• Mais
para:
tarde,
Rydberg
generalizou
1  RH
=
λ  h
a
equação
de
Balmer
 1 − 1 
 2
 n1 n22 
onde RH é a constante de Rydberg (1,096776 x 107 m-1), n1 e n2 são números
inteiros (n2 > n1).
Diagrama de níveis de energia do hidrogênio: transições de Paschen,
Balmer e Lyman
O Modelo Atômico de Bohr - 1913
Um elétron, enquanto em movimento em uma órbita
fechada, não absorve nem emite radiação. Bohr admitiu que para
cada elétron existe mais de uma órbita estável correspondente a
um nível energético diferente.
Somente são permissíveis as órbitas eletrônicas para as
quais o momento angular do elétron é um múltiplo inteiro de
h/2π, em que h é a constante de Planck.
O momento angular de uma partícula movendo-se em órbita circular é dado por mvr,
em que m é a massa, v a velocidade e r o raio do círculo. O segundo postulado requer
que as órbitas estacionárias satisfaçam a condição mvr = nh / 2π
O Modelo Atômico de Bohr - 1913
O elétron pode saltar de uma órbita para outra, desde que a
passagem seja acompanhada da emissão ou absorção de um quantum
de energia radiante, cuja freqüência é determinada pela relação:
h.ν = Ei - Ef
onde Ei - Ef representam os valores da energia do átomo no estado inicial e final,
respectivamente .
Como os estados de energia são quantizados,
a luz emitida por átomos excitados deve ser
quantizada e aparecer como espectro de
linhas. Bohr mostrou que:
(
E = − 2 . 18 × 10
−18
)
 1 
J

2
n 
onde n é o número quântico principal (por
exemplo, n = 1, 2, 3, … )
O Modelo Atômico de Bohr - 1913
• A primeira órbita tem n = 1, é a mais
próxima do núcleo e convencionou-se que
ela tem energia negativa.
• A órbita mais distante no modelo de Bohr
tem n próximo ao infinito e corresponde à
energia zero.
• Os elétrons no modelo de Bohr podem se
mover apenas entre órbitas através da
absorção e da emissão de energia em
quantum (hν).
∆E = hν =
hc
λ
(
= − 2 . 18 × 10
− 18
 1
1
J  2 −f
2
n
n
i
f
 f
i
)




Quando ni > nf, a energia é emitida.
Quando nf > ni, a energia é absorvida
Exercício
Calcule o comprimento de onda (em nm) de um fóton emitido pelo átomo de
hidrogênio quando um elétron decai de um estado onde o n = 5 para um estado
onde o n = 3. Este fóton encontra-se em qual região do espectro
eletromagnético?
h= 6,63 x 10-34J.s
Resposta
∆E = hν =
hc
λ
(
= − 2 . 18 × 10
− 18
 1
1
J  2 −f
2
n
n
f
 fi
i
)




1
1
Efóton = -2,18 x
( n2
)
2
ni
f
Efóton = - 2,18 x 10-18 J x (1/9 - 1/25)
10-18 J
Efóton = ∆E = -1,55 x 10-19 J
(negativo para indicar que libera energia)
Efóton = h x c / λ
λ = h x c / Efóton
λ = 6,63 x 10-34 (J•s) x 3,00 x 108 (m/s)/1,55 x 10-19J
λ = 1280 nm
Região do Infravermelho
Comportamento Ondulatório da Matéria
Sabendo que a luz pode se comportar como partícula,
será que a matéria pode apresentar natureza
ondulatória?
L. de Broglie
(1892-1987)
De Broglie, utilizando as equações de Einstein e de Planck,
mostrou que se os objetos são pequenos os conceitos de onda e
partículas podem ser resumidos como:
h
λ=
mv
O momento, p= mv, é uma propriedade de partícula, enquanto λ é
uma propriedade ondulatória.
Partícula
Função de onda
Exercício
Qual é o comprimento de onda (em nm) de De Broglie associado ao movimento
de uma bolinha de pingue-pongue de 2,5 g viajando a 15,6 m/s?
h= 6,63 x 10-34 J.s
1J = Kg. m2.s-2
Resposta
λ = h/m.v
λ = 6,63 x 10-34 / (2,5 x 10-3 x 15,6)
λ = 1,7 x 10-32 m = 1,7 x 10-23 nm
Comprimento de onda muito pequeno para ser detectado
O Princípio da Incerteza de Heisenberg
Na escala de massa de partículas atômicas, não podemos
determinar exatamente a posição, a direção do movimento e a
velocidade simultaneamente.
• Para os elétrons: não podemos determinar seu momento e sua
posição simultaneamente.
• Se ∆x é a incerteza da posição e ∆mv é a incerteza do momento,
então:
h
∆x·∆mv ≥
4π
W. Heisenberg
1901-1976
O Modelo Atômico Quântico
Em 1926, Schröndinger escreveu uma equação que
descrevia o comportamento partícula/onda do elétron no
átomo de Hidrogênio:
Η Ψ = EΨ
E. Schrödinger
1887-1961
A função de onda (Ψ) descreve a energia de um determinado elétron e a
probabilidade de encontrá-lo em um determinado volume do espaço.
Essa equação resulta em inúmeras soluções matemáticas,
chamadas de função de onda. Para cada FUNÇÃO DE ONDA existe
uma ENERGIA associada.
A equação só pode ser resolvida exatamente para o átomo de
hidrogênio. Para átomos multi-eletrônicos, a solução é aproximada.
O Modelo Atômico Quântico
•
Somente certas vibrações podem ser observadas numa corda
vibrante. Por analogia o comportamento do elétron no átomo é
descrito da mesma forma – somente são permitidas certas
funções de onda. Quantização surge naturalmente....(analogia
com as cordas)
•
Cada função de onda (Ψ) corresponde a energia permitida para o
elétron e concorda com o resultado de Bohr para o átomo de H.
•
Cada função de onda (Ψ) pode ser interpretada em termos de
probabilidade e (Ψ2) dá a probabilidade de encontrar o elétron
numa certa região do espaço.
•
A solução da equação ou função de onda (Ψ) descreve um estado
possível para o elétron no átomo denominado de ORBITAL.
•
Cada função de onda, ou seja, cada Orbital, é descrito por
NÚMEROS QUÂNTICOS, que nos informam ENERGIA, FORMA E
TAMANHO
Os Números Quânticos
A equação de Schrödinger necessita de quatro números
quânticos:
Ψ = fn (n, l, ml, ms)
1 - Número quântico principal, n.
Este é o mesmo n de Bohr. À medida que n aumenta, o
orbital torna-se maior e o elétron passa mais tempo mais distante
do núcleo.
n = 1, 2, 3, 4, 5 ...
n=1
n=2
n=3
n=4
Os Números Quânticos
2 - O número quântico azimutal, l.
Esse número quântico depende do valor de n e representa a
forma espacial da subcamada do orbital.
Os valores de l começam de 0 e aumentam até n-1.
Normalmente utilizamos letras para designar o l (s, p, d e f para l =
0, 1, 2, e 3).
Valor de l
símbolo da subcamada
nº elétrons
0
s (sharp)
2
1
p (principal)
6
2
d (diffuse)
10
3
f (fundamental)
14
Os Números Quânticos – Formatos dos Orbitais s
l = 0 (orbital s)
• Todos os orbitais s são esféricos.
• À medida que n aumenta, os
orbitais s ficam maiores.
• À medida que n aumenta,
aumenta o número de nós.
• Um nó é uma região no espaço
onde a probabilidade de se
encontrar um elétron é zero.
• Em um nó, Ψ2 = 0
• Para um orbital s, o número de
nós é n-1.
Os Números Quânticos – Formatos dos Orbitais p
l = 1 (orbital p)
Quando l = 1, existe um plano
NODAL que passa pelo núcleo.
Plano Nodal: Ψ passa pelo zero
• Existem três orbitais p, px, py, e
pz.
• Os três orbitais p localizam-se
ao longo dos eixos x-, y- e z- de
um sistema cartesiano.
• As letras correspondem aos
valores permitidos de ml, -1, 0,
e +1.
• Os orbitais têm a forma de
halteres.
• À medida que n aumenta, os
orbitais p ficam maiores.
• Todos os orbitais p têm um nó
no núcleo
Os Números Quânticos – Formatos dos Orbitais d
l = 2 (orbital d)
Quando l = 2, existem dois planos NODAIS
que passam pelo núcleo
• Existem cinco orbitais d
• Três dos orbitais d encontram-se em um plano bissecante aos eixos x-, y- e z.
• Dois dos orbitais d se encontram em um plano alinhado ao longo dos eixos x-,
y- e z.
• Quatro dos orbitais d têm quatro lóbulos cada.
• Um orbital d tem dois lóbulos e um anel.
Os Números Quânticos – Formatos dos Orbitais f
l = 3 (orbital f)
Os Números Quânticos
3 - O número quântico magnético, ml.
Esse número quântico depende de l. O número quântico
magnético tem valores inteiros entre -l e +l.
Fornecem a
orientação do orbital no espaço.
Existem 2l+1 valores diferentes de ml para cada valor de l
e, portanto, 2l+1 orbitais em uma subcamada de número
quântico l.
Ex:
l = 1 – ml = +1, 0, -1
l = 2 – ml = +2, +1, 0, -1, -2
Orbitais e Números Quânticos
Os Números Quânticos
4 - O número quântico de spin, ms.
Experimentos mostraram que as linhas espectrais do H e
outros elementos se desdobravam quando submetidos a um campo
magnético. O elétron se comportava como se tivesse uma rotação
(spin) própria em torno do seu eixo
ms = +½
ms = -½
Paramagnetismo e Diamagnetismo
•Sal de cozinha, giz,
tecidos
–
são
repelidos
pela
aproximação de um
imã: Diamagnéticos
Paramagnético
Elétrons desemparelhados
2p
Diamagnético
Todos elétrons emparelhados
2p
•Metais
–
são
atraídos
pela
aproximação de um
imã:
Paramagnéticos
Os Números Quânticos - Resumo
A Energia dos Orbitais
• Um orbital pode ser ocupado por no máximo 2 elétrons
• Pelo princípio da exclusão de Pauli: dois elétrons não podem ter a
mesma série de 4 números quânticos. Portanto, dois elétrons no
mesmo orbital devem ter spins opostos.
• De acordo com as regras de Hund:
- Os orbitais são preenchidos em ordem crescente de n.
- Dois elétrons com o mesmo spin não podem ocupar o mesmo
orbital (Pauli).
- Para os orbitais degenerados (de mesma energia), os elétrons
preenchem cada orbital isoladamente antes de qualquer orbital
receber um segundo elétron (regra de Hund).
A Energia dos Orbitais em um Átomo Monoeletrônico
Energia depende apenas do número quântico n
n=3
n=2
En = -RH (
n=1
1
n2
)
SINAL NEGATIVO:
significa que a energia do elétron
em um átomo é MENOR que a
energia do elétron livre
A Energia dos Orbitais em um Átomo Polieletrônico
Energia depende de n e l
n=3 l = 2
n=3 l = 1
n=3 l = 0
n=2 l = 0
n=1 l = 0
n=2 l = 1
A Energia dos Orbitais em um Átomo Polieletrônico
A que se deve essa ordem de energia dos orbitais
em átomos polieletrônicos?
1 - Efeito de penetração dos orbitais:
s > p > d > f .......
Quanto maior a
probabilidade de
encontrar o elétron
perto do núcleo, mais
ele é atraído pelo
núcleo, maior o poder
de penetração do
orbital
2 - Efeito de blindagem: elétrons mais
internos blindam os elétrons mais
externos da atração pelo núcleo
Quanto maior o poder de penetração do orbital,
os seus elétrons exercem maior blindagem sobre
os elétrons mais externos
Ordem de Preenchimento dos Orbitais
Diagrama de Pauling (Aufbau)
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s
Notação da Configuração Eletrônica
Notação spdf - espectroscópica
Notação em caixa
Ex: H, Z = 1
1
1s
Valor de n
Ex: He, Z = 2
no. de elétrons
Valor de l
1s
Configuração eletrônica:
• descreve o arranjo dos elétrons em um átomo
• o arranjo do estado fundamental é aquele que
apresenta a menor energia possível
• o arranjo de menor energia é o mais estável
Direção das
setas indicam a
orientação do
spin dos
elétrons
Configuração Eletrônica na Tabela Periódica
L tio - Li
Lítio
Grupo 1A
Z=3
1s22s1 ---> 3 elétrons
3p
3s
2p
2s
1s
Ber lio - Be
Berílio
Grupo 2A
Z=4
1s22s2 ---> 4 elétrons
3p
3s
2p
2s
1s
Boro -B
Grupo 3A
Z=5
1s2 2s2 2p1 ---> 5 elétrons
3p
3s
2p
2s
1s
Carbono -C
Grupo 4A
Z=6
1s2 2s2 2p2 ---> 6 elétrons
3p
3s
2p
2s
1s
Por quê não emparelhar o elétron?
Regra de HUND
Nitrogênio - N
Grupo 5A
Z=7
1s2 2s2 2p3 ---> 7 elétrons
3p
3s
2p
2s
1s
Oxigênio -O
Grupo 6A
Z=8
1s2 2s2 2p4 ---> 8 elétrons
3p
3s
2p
2s
1s
Fluor - F
Grupo 7A
Z=9
1s2 2s2 2p5 ---> 9 elétrons
3p
3s
2p
2s
1s
Neônio - Ne
Chegamos no final do
segundo período!!!!!
Grupo 8A
Z = 10
1s2 2s2 2p6 ---> 10 elétrons
3p
3s
2p
2s
1s
Sódio - Na
Grupo 1A
Z = 11
1s2 2s2 2p6 3s1 or
“elétrons internos do Ne” + 3s1
[Ne] 3s1 (notação de gás nobre)
Iniciou-se um novo período
Todos os elementos do grupo 1A tem a configuração [elétrons
internos] ns1.
Elétrons de valência
Alumínio - Al
Grupo 3A
Z = 13
1s2 2s2 2p6 3s2 3p1
[Ne] 3s2 3p1
Elétrons de valência
3p
3s
2p
2s
1s
Fósforo - P
Grupo 5A
Z = 15
1s2 2s2 2p6 3s2 3p3
[Ne] 3s2 3p3
3p
3s
2p
2s
1s
Formação de Cátions e Ânions – Elementos Representativos
Na [Ne]3s1
Na+ [Ne]
Ca [Ar]4s2
Ca2+ [Ar]
Al [Ne]3s23p1
Al3+ [Ne]
Átomo ganha elétrons
de modo que o ânion
venha a ter
configuração de gás
nobre
Átomo perde elétrons de
modo que o cátion venha a
ter uma configuração
eletrônica de gás nobre.
H 1s1
H- 1s2 ou [He]
F 1s22s22p5
F- 1s22s22p6 ou [Ne]
O 1s22s22p4
O2- 1s22s22p6 ou [Ne]
N 1s22s22p3
N3- 1s22s22p6 ou [Ne]
Metais de transição
Todos os elementos do 4º período tem configuração [Ar]nsx(n - 1)dy e, portanto,
são elementos do bloco d.
Orbitais 3d usados do Sc-Zn
Distribuição Eletrônica para Metais de Transição
Z=21 - [Ar] 4s2 3d1 -------Sc
Z=22 - [Ar] 4s2 3d2 -------Ti
Por quê o orbital 4s é
preenchido antes do 3d?
O orbital s é mais penetrante e,
conseqüentemente, os elétrons sentem menos
a presença dos outros. Por estar mais próximo
ao núcleo, a energia é mais baixa (mais
negativa), fazendo com que um elétron 4s
tenha energia menor do que um 3d.
Z=23 - [Ar] 4s2 3d3 --------V
Z=24 - [Ar] 4s1 3d5 --------Cr
Z=25 - [Ar] 4s2 3d5 -------Mn
Z=26 - [Ar] 4s2 3d6 --------Fe
Z=27 - [Ar] 4s2 3d7 --------Co
Z=28 - [Ar] 4s2 3d8 --------Ni
Z=29 - [Ar] 4s1 3d10 -------Cu
Z=30 - [Ar] 4s2 3d10 -------Zn
Por quê o orbital 4s do Cr e Cu
é semi-preenchido ?
Distribuição Eletrônica para Metais de Transição
A resposta à esta questão está na estabilidade extra que
uma camada cheia (ou semi-cheia) proporciona.
Camada semi-cheia d5
Ocupação
simétrica
Camada cheia d10
O emparelhamento de elétrons em um
mesmo orbital envolve repulsão a qual
aumenta a energia do orbital.
Estabilidade extra
Por essa razão, o elétron ocupa os orbitais d vazios, gerando uma
camada semi-cheia (ou cheia) e, assim, ganha estabilidade extra devido a
diminuição de energia.
Distribuição Eletrônica para Metais de Transição
Na formação de cátions, inicialmente são removidos elétrons da camada
ns e depois elétrons da camada(n - 1).
Ex: Fe [Ar] 4s2 3d6
perde inicialmente 2 elétrons ---> Fe2+ [Ar] 4s0 3d6
Fe2+
Fe
4s
3d
4s
3d
Fe3+
4s
3d
Distribuição Eletrônica para Lantanídeos
Todos estes elementos tem configuração [elétrons internos]nsx(n - 1)dy(n - 2)fz e
são chamados de elementos do bloco f
Orbitais 4f usados para
Ce - Lu e 5f para Th - Lr
Configuração Eletrônicas dos Elementos