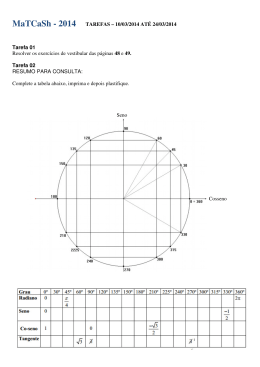
Matemática II
AULA
Prof. Sérgio Tambellini
12
Arcos côngruos na circunferência
Expressão geral dos arcos trigonométricos:
Para representar todas as medidas reais dos arcos côngruos
de uma sequência usa-se a expressão:
Tópicos da aula
 Medidas positivas e negativas
 Arcos côngruos
 Expressão geral dos arcos trigonométricos
x    k.r , k  Z
Resumo teórico
Medidas positivas e negativas:
As medidas dos arcos tomadas no sentido anti horário, a
partir da origem, assumem sinais positivos para suas
medidas.
2o quadrante
100o
onde,
x : é a medida real de qualquer uma das medidas dos arcos
côngruos.
 : é a primeira medida não negativa dos arcos côngruos.
k : é um contador inteiro de razões.
r : é a razão, ou seja, a distância entre duas medidas
consecutivas da sequência dos arcos côngruos.
1o quadrante
0o (origem)
195o 
3o quadrante
Exemplo:
4o quadrante
A
270o  630o  - 90o  - 450o  ...
As medidas dos arcos tomadas no sentido horário, a partir
da origem, assumem sinais negativos para suas medidas.
Colocando em ordem crescente as extremidades dos arcos
côngruos com vértices em A , tem-se:
2o quadrante
- 195o
1o quadrante


( ... , - 450o , - 90o , 270o , 450o , ... )
0o (origem)
r = 360o
- 100 
o
3o quadrante
A expressão geral dos arcos côngruos em A é dada por
4o quadrante
x = 270o + k.360o , k  Z
Arcos côngruos:
Arcos côngruos são os arcos cujas extremidades são
coincidentes, quer sejam tomadas no sentido anti horário
como no sentido horário.
Exercícios de aula
1) Escreva a expressão geral dos arcos côngruos ao arco de
medida 30o.
80o  440o  800o  - 280o  ...

 30

270o  630o  - 90o  - 450o  ...
26
o
2) Escreva a expressão geral dos arcos côngruos ao arco de
medida - 60o.
5) Escreva a expressão geral dos arcos que têm
extremidades em Eou em F, simétricos com relação ao
eixo vertical.
(135o) F

E (45o)
- 60o
3) Escreva a expressão geral dos arcos que têm
extremidades em A ou em B, separados diametralmente.
6) Escreva a expressão geral dos arcos que têm
extremidades em um dos vértices do triângulo equilátero
inscrito na circunferência, dado na figura abaixo.
A (60o)
(240o) B
270o
4) Escreva a expressão geral dos arcos que têm
extremidades em C ou em D, simétricos com relação ao
eixo horizontal.
7) Escreva as expressões obtidas nos exercícios (1), (2),
(3), (3), (4), (5) e (6) com as medidas em radianos,
C (20o)
D (340o)
27
8) Escreva a expressão geral dos arcos que têm
extremidades em um dos vértices do retângulo inscrito na
circunferência abaixo, sabendo que os arcos são arcos
simétricos com relação aos eixos horizontal e vertical.
Tarefa de casa
 5

1) (PUC) Sendo  um ângulo, então 
   pertence ao
2


a) 1o quadrante.
d) 4o quadrante.
b) 2o quadrante.
e) n.d.a.
c) 3o quadrante.
30o
2) (Fund. Educ, Serra dos Órgãos) Marcando no círculo
trigonométrico as extremidades dos arcos da forma k.50o,
k inteiro, obtemos os vértices de um polígono regular cujo
número de lados é igual a
a) 7.
d) 29.
b) 8.
e) 36.
c) 16.
3) Representar no círculo trigonométrico as imagens dos
números reais x, tais que x = 210o + k.360o , k  Z.
4) Representar no círculo trigonométrico as imagens dos
2
 k. , k  Z .
números reais x, tais que x 
3
5) Representar no círculo trigonométrico as imagens dos
números reais x, tais que x =  45o + k.360o , k  Z.
6) Representar no círculo trigonométrico as imagens dos
2
, kZ .
números reais x, tais que x  k.
5
9) Escreva a expressão geral dos arcos (em radianos) que
têm extremidades em um dos vértices do triângulo
equilátero inscrito na circunferência, dado na figura
abaixo.

Questão de raciocínio lógico
Em torno de uma mesa quadrada, encontram-se sentados
quatro sindicalistas. Oliveira, o mais antigo entre eles, é
mineiro. Há também um paulista, um carioca e um baiano.
Paulo está sentado à direita de Oliveira. Norton, à direita
do paulista. Por sua vez, Vasconcelos, que não é carioca,
encontra-se à frente de Paulo. Assim,





a) Paulo é paulista e Vasconcelos é baiano.
b) Paulo é carioca e Vasconcelos é baiano.
c) Norton é baiano e Vasconcelos é paulista.
d) Norton é carioca e Vasconcelos é paulista.
28