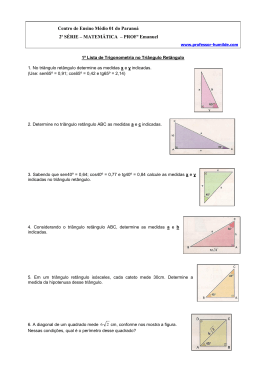
AULA 09 - TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
1. No triângulo retângulo determine as medidas x e y indicadas.
(Use: sen65º = 0,91; cos65º = 0,42 e tg65º = 2,14)
2. Determine no triângulo retângulo ABC as medidas a e c indicadas.
3. Sabendo que sen40º = 0,64; cos40º = 0,77 e tg40º = 0,84 calcule as medidas x e y indicadas no triângulo retângulo.
4. Considerando o triângulo retângulo ABC, determine as medidas a e b indicadas.
6. A diagonal de um quadrado mede 6 2 cm, conforme nos mostra a figura.
Nessas condições, qual é o perímetro desse quadrado?
-1-
 Aula 09 Trigonometria no Triângulo retângulo – Prof. Cirço Mancilla
5. Em um triângulo retângulo isósceles, cada cateto mede 30cm. Determine a medida da hipotenusa desse triângulo.
AULA 09 - TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
7. Uma pipa é presa a um fio esticado que forma um ângulo de 45º com o solo. O comprimento do fio é 80m. Determine a
altura da pipa em relação ao solo. Dado
2 = 1,41
8. Qual é o comprimento da sombra de uma árvore de 5 m de altura quando o sol está 30º acima do horizonte?
Dado
3 = 1,73
9. Determine a altura do prédio da figura seguinte:
10. Para determinar a altura de um edifício, um observador coloca-se a 30m de distância e assim o observa segundo
-2-
3=
 Aula 09 Trigonometria no Triângulo retângulo – Prof. Cirço Mancilla
um ângulo de 30º, conforme mostra a figura. Calcule a altura do edifício medida a partir do solo horizontal. Dado
1,73
AULA 09 - TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
11. Observe a figura e determine:
a) Qual é o comprimento da rampa?
b) Qual é a distância do inicio da rampa ao barranco?
12. A uma distância de 40m, uma torre é vista sob um ângulo
α = 30º.
α , como mostra a figura. Determine a altura h da torre se
13. Em um triângulo ABC, retângulo em A, o ângulo B mede 30º e a hipotenusa mede 5cm. Determine as medidas dos
catetos AC e AB desse triângulo.
a) 44,7
b) 48,8
c) 54,6
d) 60,0
e) 65,3
15. (PUCCAMP) Uma pessoa encontra-se num ponto A, localizado na base de um prédio, conforme mostra a figura
adiante. Se ela caminhar 90 metros em linha reta, chegará a um ponto B, de onde poderá ver o topo C do prédio, sob
um ângulo de 60°. Quantos metros ela deverá se afastar do ponto A, andando em linha reta no sentido de A para B,
para que possa enxergar o topo do prédio sob um ângulo de 30°?
a) 150
b) 180
c) 270
d) 300
e) 310
-3-
 Aula 09 Trigonometria no Triângulo retângulo – Prof. Cirço Mancilla
14. (VUNESP) Uma pessoa, no nível do solo, observa o ponto mais alto de uma torre vertical, à sua frente, sob o
ângulo de 30º. Aproximando-se 40 metros da torre, ela passa a ver esse ponto sob o ângulo de 45º. A altura
aproximada da torre, em metros, é
AULA 09 - TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
16. (PUCCAMP) A figura a seguir é um corte vertical de uma peça usada em certo tipo de máquina. No corte aparecem
dois círculos, com raios de 3cm e 4cm, um suporte vertical e um apoio horizontal. A partir das medidas indicadas na
figura, conclui-se que a altura do suporte é:
a) 7cm
b) 11cm
c) 12cm
d) 14cm
e)16 cm
17. (UFRS) Um barco parte de A para atravessar o rio. A direção de seu deslocamento forma um ângulo de 120° com a
margem do rio. Sendo a largura do rio 60m, a distância, em metros,
percorrida pelo barco foi de:
a) 40 2
b) 40 3
c) 45 3
d) 50 3
e) 60 2
18. Um observador vê um edifício, construído em terreno plano, sob um ângulo de 60º. Se ele se afastar do edifício
mais 30m, passará a vê-lo sob ângulo de 45º. Calcule a altura do edifício.
(
)
3
20. (FUVEST) A raiz da equação cos 2 α x 2 − (4 cos α .senβ ) x +   senβ = 0 é x = 1, sendo α e β os ângulos indicados
2
no triângulo retângulo da figura.
Calcule as medidas de α e β.
-4-
 Aula 09 Trigonometria no Triângulo retângulo – Prof. Cirço Mancilla
19. Determine na figura a área do triângulo BCD e a medida do segmento AD .