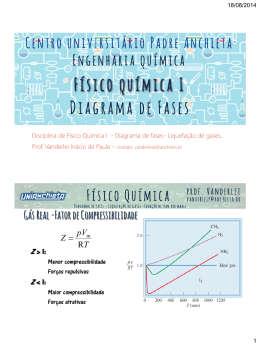
LOQ - 4007 Físico-Química
Capítulo 1: Propriedades dos Gases
Gases Reais
Atkins & de Paula (sétima edição)
Profa. Dra. Rita de Cássia L.B. Rodrigues
Departamento de Biotecnologia – LOT
E-mail: [email protected] ou [email protected]
Fone: 3159-5027
Aula 2 - Gases Reais
»
»
»
1. Interações moleculares
(a) O fator de Compressibilidade
(b) Coeficientes do virial
(c) Condensação
(d) Coordenadas críticas
2. Equação de van der Waals
(a) A fidedignidade da equação
(b) As características da equação
3. O princípio dos estados correspondentes
LISTA DE EXERCÍCIOS
Capítulo 1 – Atkins (sétima edição)
Gases Reais
Conceitos importantes: abordagem

Fator de compressibilidade

Coeficientes do virial

Equação de estado do virial

Temperatura Boyle do gás

Pressão de vapor

Coordenadas críticas

Ponto crítico

Temperatura crítica, Tc

Pressão crítica, Pc

Volume molar crítico, Vc

Fluido supercrítico

Equação de van der Waals

Constantes de van der Waals

Ondulações de van der Waals

Construção de Maxwell

Fator de compressibilidade
no ponto crítico, Zc

Coordenadas reduzidas

Princípio dos estados
correspondentes
Gases Reais

Os gases reais não obedecem exatamente
à lei dos gases perfeitos.

Os desvios são particularmente notáveis
nas pressões elevadas e nas temperaturas
baixas, especialmente quando o gás está a
ponto de se condensar num líquido.
Visualizar nas figuras a seguir...
Gases Reais
As linhas retas sugerem
que, a pressão constante, o
volume de um gás é
diretamente proporcional à
sua temperatura, desde que
a temperatura seja expressa
nas unidades adequadas.
Gases Reais

1.
2.
Equação do gás ideal é válida para gases
que têm as seguintes propriedades:
As moléculas do gás têm um volume
desprezível
não existe interação atrativa ou repulsiva
entre as moléculas
ESTES GASES NÃO EXISTEM
Apesar disto a equação: PV=nRT é bastante útil para
muitos gases em temperaturas altas e pressão
moderadamente baixa (≤ 10 atm)
1. Interações Moleculares

Gases reais exibem desvios em relação à lei
dos gases perfeitos em virtude das
INTERAÇÕES MOLECULARES

As forças repulsivas entre as moléculas
contribuem para EXPANSÕES e

As forças atrativas para COMPRESSÕES
1. Interações Moleculares
Forças repulsivas:

Notáveis somente quando as
moléculas estão quase em contato.

Interações de curto alcance, mesmo
numa escala medida em diâmetros
moleculares (Figura ao lado). Assim,
só se tornam significativas quando as
distâncias entre as moléculas é
pequena.
Ex. um gás sob pressão elevada, em que
um grande número de moléculas
ocupa volume relativamente pequeno.
1. Interações Moleculares
Forças atrativas:

Têm alcance relativamente grande
e se manifestam a distâncias de
diversos diâmetros moleculares.

São importantes quando as
moléculas estão relativamente
próximas umas das outras, mas
não necessariamente se tocando
(figura ao lado).

Não são efetivas quando as
moléculas estão muito separadas
1. Interações Moleculares
Forças intermoleculares podem ser importantes:
 Temperatura tão baixa = as moléculas se
movem com velocidades médias pequenas e
uma pode ser capturada por outra.
Forças intermoleculares insignificantes:
 Pressões baixas = quando a amostra de gás
ocupa um volume grande, as moléculas estão
tão afastadas umas das outras. O gás se
comporta como gás perfeito
1. Interações Moleculares
Forças atrativas X Forças repulsivas

Pressões médias = moléculas afastadas por
alguns poucos diâmetros moleculares, as
forças atrativas dominam as repulsivas. Neste
caso, gás mais compressível que o gás
perfeito, pois as forças contribuem para
aproximação das moléculas.

Pressões elevadas = moléculas estão muito
próximas umas das outras e o gás é menos
compressível que o gás perfeito, em virtude
da ação que tende a afastar as moléculas.
Quando um gás se desvia
apreciavelmente do
comportamento ideal?
Quando o gás é comprimido porque
suas moléculas se aproximam muito
uma das outras
Qual a forma de medir esse
desvio da condição ideal?
Deve-se fazer um gráfico do fator de
compressibilidade (Z) do gás em
função de sua pressão)
a) O fator de compressibilidade
Nas mesmas pressão e temperatura
volume molar do gás
Vm
Z
 0
volume molar de um gás perfeito Vm
PVm  RTZ
como
RT
V 
P
o
m
Volume molar de um gás perfeito
PVm
Z
RT
Expressão equivalente ao volume molar de um gás perfeito
a) O fator de compressibilidade
Gráfico de Z contra a pressão = investigar a
dependência das forças intermoleculares
em relação à distância

Gás perfeito = Z=1 (quaisquer condição)
O desvio de Z em relação a 1 é uma medida
do afastamento do gás em relação ao
comportamento ideal.
Depende da pressão:
a) O fator de compressibilidade
Depende da pressão:



Z≈1 (pressões muito baixas) todos
os gases comportam-se como
perfeitos.
Z>1 (pressões elevadas) mostra que
tem um volume molar maior que um
gás perfeito. As forças repulsivas
são dominantes.
Z<1 (pressões intermediárias)
indica que as forças atrativas estão
reduzindo o volume molar em
comparação com o de um gás
perfeito.
Qual é a outra forma de
representar a não idealidade
de um gás?
Equação virial de estado: onde o fator de
compressibilidade (Z) é expresso como
uma expansão em série de potências
inversas do volume molar Vm
 B C

pV  RT 1 

 .......
 V V

m
2
m
m
EQUAÇÃO DE ESTADO DO VIRIAL =
Este nome vem da palavra latina para força (intermolecular)
b) Coeficientes do virial
»
Esta expressão é um exemplo comum em físicoquimica, em que se transforma uma expressão
simples (no caso a expressão pV=nRT) no primeiro
termo de uma série de potências de uma variável
(no caso o Vm)
 B C

pV  RT 1 

 .......
 V V

m
2
m
m
B, C, D...1º, 2º...coeficientes do virial
1º coeficiente = 1
1º, 2º...e os mais altos são todos dependentes da Temperatura
Para um gás ideal o 2º e os coeficientes viriais mais altos
são zero (Pv=nRT)
b) Coeficientes do virial
»
Outra alternativa da equação do virial é dada por
uma expansão em série do fator de
compressibilidade em termos da pressão, P:
pVm  RT (1  B' p  C ' p 2  ...)
Como P e V são relacionados, não é surpreendente que
existam relações entre B e B´, C e C´ e assim por diante
Em cada equação, os valores dos coeficientes descrescem
rapidamente B´>>C´>>D´…De forma que passa para
pressões, digamos entre zero e 10 atm e precisamos incluir
somente o segundo termo, sob a condição de que a T não
seja muito baixa.
Como são determinados esses
coeficientes viriais?
Para determinado gás, eles são
calculados a partir de um conjunto PV-T de dados do gás por meio de um
procedimento de ajuste de curvas
usando um computador
(experimentalmente)
b) Coeficientes do virial
Isotermas do dióxido de carbono
levantadas experimentalmente.
» Nas temperaturas elevadas
(>50°C) e volumes molares
grandes (Vm > 0.3 L/mol), as
isotermas reais pouco diferem
das isotermas do gás perfeito.
» As pequenas diferenças
sugerem que a lei do gás
perfeito, seja, de fato, a
primeira parcela de uma
expressão da forma:
pVm  RT (1  B' p  C ' p 2  ...)
CO2
b) Coeficientes do virial (continuação)

Coeficientes determinados experimentalmente (see Atkins, Table 1.3)
»
30 coeficiente tem menor importância do que o 20, etc.
 B/Vm

>> C/Vm2
Para misturas, coeficientes dependem da fração molar
»
B = x12B11 + 2 x1x2B12 + x22B22
»
x1x2B12 representa a interação entre gases
2nd Virial Coefficients
Equimolar Mixtures of CH4 and CF4
K
273.15
298.15
373.15
B1(CH4)
(cm3/mol)
-53.35
-42.82
-21.00
B1(CH4)
(cm3/mol)
-111.00
-88.30
-43.50
B12
(cm3/mol)
-62.07
-48.48
-20.43
b) Coeficientes do virial (continuação)

O fator de compressibilidade, Z, é uma função de p (veja figura anterior) e T
»
Para gás ideal dZ/dp (coeficiente angular da curva) = 0

»
Porque?
Para gás real, dZ/dp pode ser determinado utilizando a equação do virial

Substituindo Vm por (Vm = Z Vm°); e Vm°=RT/p

Coeficiente angular = B’ + 2pC’+ ….

Como
p o
, dZ/dP
B’, que não é necessariamente 0. Então a
inclinação da curva de Z em função de p não se aproxima,
necessariamente de 0 (o valor correspondente ao gás ideal). Como muitas
propriedades do gás dependem das derivadas (veremos a diante), as
propriedades dos gases reais nem sempre coincidem com as do gás ideal
nas pressões baixas (

p o
).
Raciocínio semelhante mostra que
quando Vm
dZ
B
d( 1
Vm )
 correspondendo a
p o
b) Coeficientes do virial (continuação)
»
Como os coeficientes do virial só dependentem da temperatura,
pode haver uma temperatura em que Z
1 com o coeficiente
angular nulo em pressões baixas ou volumes molares grandes
(próxima figura ).
»
Nesta temperatura, chamada de TEMPERATURA BOYLE do gás,
TB , as propriedades do gás real coincidem com as do gás perfeito
nas pressões baixas ( p  o ).
»
De acordo com a equação
nulo
dZ
B
d( 1
Vm )
o coeficiente angular de Z será
Quando p  o
e se o B for nulo, podemos concluir que B=0 na
TEMPERATURA BOYLE . Segue então, de acordo com a equação
 B C

pV  RT 1 

 .......
 V V

m
2
m
»
m
Que pVm≈RTB sobre uma faixa de pressões mais amplas do que em
qualquer outra temperatura, pois o primeiro termo da equação do virial
depois do 1 (B/Vm) é nulo e as parcelas seguintes C/Vm2,...., são
desprezívelmente pequenas
 Na TB , B’
0 e, desde que os termos remanecentes na equação do
virial são pequenos , p Vm = RT para o gás real
b) Coeficientes do virial (continuação)

Em baixas T: inicialmente dZ/dp < 0,
B é negativo

Em elevadas T: inicialmente dZ/dp > 0,
B é positivo
(corresponde ao coeficiente de primeira
ordem B nestas temperaturas)

A temperatura na qual o coeficente angular
é zero corresponde a TEMPERATURA
BOYLE, TB, onde B = 0 (gás real
corresponde a um gás ideal)
c) Condensação
CO2
Análise de uma amostra de gás, inicialmente no ponto A
após sua compressão a uma temperatura constante
(ação de um pistão)
(movimento no gráfico á esquerda do ponto A)
Na vizinhança de A, P se eleva seguindo aprox. a lei de
Boyle. Desvios grandes nesta lei aparecem quando o volume atinge o
do ponto B.
»
Em C (60 atm para o CO2) desaparece qualquer semelhança
com um gás perfeito, pois abruptamente o pistão se desloca sem
provocar aumento de pressão. Este comportamento representado
pelo seguimento CDE.
»
No vaso em que se faz a compressão á esquerda de C aparece
uma gota de líquido e há duas fases separadas por uma fronteira
nítida.
Quando o volume diminiu de C passando D até E, a
quantidade de líquido aumenta. Não há resistência do pistão, o
gás condensa e o volume diminui.
»
A pressão correspondente ao seguimento da reta CDE (líquido e
vapor em equilíbrio) =PRESSÃO DE VAPOR do líquido na
temperatura da experiência.
»
Em E, amostra inteiramente liquefeita e o pistão encostado
na superfície do líquido, e para redução de volume é necessário
exercer uma pressão muito grande (seguimento ascendente em E
para F)
»
2 phases
d) Coordenadas críticas
CO2
Na teoria dos estados da matéria, a isoterma
na temperatura Tc tem relevância especial
(no caso do CO2 =Tc= 304,19 K ou 31,04 °C)

Numa isoterma pouco abaixo de Tc, o
comportamento do gás é semelhante ao
que descrevemos: a uma certa pressão,
2 phases
há condensação do gás em líquido e as
duas fases são bem separadas por uma
fronteira nítida.
d) Coordenadas críticas

Mas, se a condensação for feita na própria
Tc, não aparece a fronteira que separa as
duas fases e os volumes, em cada
extremidade do seguimento horizontal da
isoterma, se confundem e definem um
único ponto, o PONTO CRÍTICO do gás.

A temperatura, a pressão e volume molar
no ponto crítico são chamados pc, Vc e Tc
são as coordenadas críticas da
substância.

Na Tc ou acima dela, a amostra tem uma
única fase que ocupa todo o volume do
recipiente. Esta fase por definição é um
gás.
CO2
2 phases
d) Coordenadas críticas
Analise o caso do oxigênio que tem Tc = 154,8 K.
É possível produzir oxigênio líquido pela simples
compressão do gás acima desta temperatura?
O que seria necessário fazer para liquefazer o oxigênio?

Para liquefazer o oxigênio, ou seja, obter uma fase fluida que não
ocupe todo o volume do recipiente será preciso inicialmente resfriálo abaixo de 154,8 K e depois então comprimi-lo isotermicamente.

A única fase que enche todo o volume do recipiente que
contém a substância quando T>Tc pode ser muito mais
densa do que a fase que consideramos, usualmente,
como sendo gasosa.
Por isso, talvez seja mais conveniente considerá-la um
FLUIDO SUPERCRÍTICO.

2. A equação de Van Der Waals
As
equações de estado do virial =
proporcionam informações objetivas
sobre o gás quando se conhecem os valores
particulares dos coeficientes.
Equação
de van der Waals: uma equação
mais geral, menos precisa, válida para todos
os gases.
2. A equação de Van Der Waals
Equação
de van der Waals:
Esta equação é um excelente exemplo da construção de um modelo
propiciada pela análise científica de um problema matemático
complicado mas fisicamente simples.
A proposta de van der Waals foi feita com base nos dados experimentais de
que dispunha, associados a considerações termodinâmicas rigorosas.
n 
RT
a
Equação de van der Waals é p  nRT  a 
  

V  nb V  V  b V
2
2
m
m
Tem termos de volume molar Vm=V/n
As constantes a e b são CONSTANTES DE VAN DER
WAALS e são características de cada gás e
independentes da temperatura
2. A Equação de Estado de vdW
em termos de Volume molar
2. A equação de Van Der Waals
2. A equação de Van Der Waals
a) A fidegnidade da equação

Examinaremos a exatidão com que a equação de van
der Waals traduz o comportamento dos gases reais.

Em trabalhos de grande exatidão = equação do
virial e dos coeficientes do virial a várias
temperaturas = análise númerica do
comportamento do sistema.

Vantagens da equação de van der Waals = é
analítica (pode ser expressa simbolicamente) e
possibilita algumas conclusões gerais sobre o
comportamento dos gases reais.
E quando a equação de van der Waals falha?
2. A equação de Van Der Waals
a) A fidegnidade da equação
E quando a equação de van der Waals falha?

Quando a equação falha é possível adotar
uma outra equação de estado, entre as
muitas outras que já foram propostas
(tabela a seguir), ou então inventar uma
nova ou buscar apoio na equação de virial.
2. A equação de Van Der Waals
a) A fidegnidade da equação
2. A equação de Van Der Waals
a) A fidegnidade da equação
A
fidegnidade da equação pode ser
analisada comparando as suas
isotermas calculadas (figuras ao lado)
com as isotermas levantadas
experimentalmente para o CO2
(apresentadas anteriormente).

As isotermas de van der Waals
são bem parecidas com as
experimentais, exceto quanto
as oscilações abaixo da
temperatura crítica (caída
brusca).
2. A equação de Van Der Waals
a) A fidegnidade da equação

Essas ONDULAÇÕES DE VAN DER
WAALS são irreais, pois mostram
comportamento impossível, no qual o
aumento de pressão provoca aumento
de volume.


Essas ondulações de van der Waals,
são substituídas por um segmento de
reta horizontal, traçado de modo que as
áreas subtendidas sobre e sob a reta
sejam iguais. Este procedimento é
chamado de CONSTRUÇÃO DE
MAXWELL .
As constantes de van der Waals são
determinadas pelo ajuste das curvas
calculadas às curvas experimentais.
2. A equação de Van Der Waals
a) A fidegnidade da equação
CO2
van der Waals @T/Tc
Ondulações de van der Waal (cont.)


Temperatura crítica do CO2 304.2 K (31.04°C)
Abaixo da Tc, ocorrem oscilações
» Ondulações de van der Waals
» Irrealista, pois sugere que aumento de p pode elevar o V
» Re-colocada com linhas retas de areas iguais ( construção de Maxwell)
2. A Equação de Estado de vdW
comparação com comportamento real
Comportamento do gás ideal
Comportamento de vdW
2. A Equação de Estado de vdW
comparação com comportamento real
Isotermas de
van der Waals
calculadas em
diversos valores de
T/Tc
2. A Equação de Estado de vdW
comparação com comportamento real
Isotermas de
van der Waals
calculadas em
diversos valores de
T/Tc
Ondulações de
van der Waals:
São irreais, pois
mostram
comportamento
impossível: o aumento
da pressão provoca
aumento do volume!
2. A Equação de Estado de vdW
comparação com comportamento real
Construção de Maxwell
2. A Equação de Estado de vdW
comparação com comportamento real
Construção de Maxwell
2. A Equação de Estado de vdW
comparação com comportamento real
Isotermas do CO2
2. A Equação de Estado de vdW
características da equação
Em T elevada e Vm grande, as
isotermas de vdW coincidem
com as isotermas do gás
perfeito.
Quando T é alta, RT é muito
grande se comparado ao valor
do segundo termo da equação
de vdW;
se o Vm for grande,
Vm>>b no primeiro termo.
A Equação de Estado de vdW
características da equação
Os líquidos e os gases coexistem
quando os efeitos de coesão e os de
dispersão estão equilibrados.
As ondulações de vdW ocorrem
quando os dois termos da equação
tem grandezas semelhantes.
O primeiro provém da energia cinética
e interações repulsivas; o segundo
representa o efeito das interações
atrativas.
2. A Equação de Estado de vdW
características da equação
As coordenadas críticas podem ser
obtidas através das constantes de van der
Waals.
As isotermas oscilam quando T<Tc;
elas convergem e em T=Tc a curva tem
inflexão com primeira e segunda
derivadas nulas. As coordenadas
podem ser calculadas através destas
derivadas.
2. Equação de van der Waals


Acima da Tc, o ajuste é bom
Abaixo da Tc, ocorre desvios
nRT
n 
RT
a
p
 a   

V  nb V  V  b V
2
2. Equação de van der Waals
m
2
m
Constantes de van der Waals
para a equação de van der Waals
gás
entre moléculas admitindo-se que cada
molécula se comporta como uma esfera pequena,
rígida e impenetrável
Ar
CO2
He
Xe
Justificativa
»Repulsão
Redução
do volume efetivo do recipiente a um
número proporcional ao número de moléculas
mutiplicado por um fator de volume maior que o
volume de uma molécula
Assim V torna-se (V-nb)


»Forças
b depende de um gás particular
He é pequeno, Xe é maior, bXe >bAr
Justificativas
Feitas no quadro...
tanto da frequência como das forças de
colisões e são proporcionais ao quadrado do volume
molar (n/V)2
Assim p torna-se p + a (n/V)2
a depende de um gás particular
 He é inerte, CO2 é menos inerte do que o He,
aCO2 >>aAr

b
(10-2 L2/ mol)
3.20
4.29
2.38
5.16
Xenônio=Xe
atrativas atuam para reduzir a pressão
Depende
a
(atm L2/ mol2)
1.337
3.610
0.0341
4.137
Justificativa da Equação de van der
Waals
Feitas no quadro...
Os coeficientes a e b são ajustados para modelar determinadas
características do comportamento de um gás, e são dependentes das
forças atrativas e repulsivas entre as moléculas no gás.
V
- nb:

Freqüência e as forças das colisões são reduzidas pelas forças de
atração, a uma força proporcional à n/V (concentração molar),
portanto, a pressão é reduzida como o quadrado dessa
concentração, e é escrito como:
-a(n/V)2 :

nb é um volume aproximado muito
pequeno ocupado pelas próprias moléculas.
a é uma constante positiva de proporcionalidade
Para a e b não devem ser atribuídas propriedades moleculares
específicas, mas sim, tê-los como coeficientes, que ajudam a
modelar com precisão o comportamento do gás, e que podem ser
designado especificamente para cada tipo de gás
2. Equação de van der Waals
nRT
n 
RT
a
p
 a   

V  nb V  V  b V
2
m
2
m
Efeito da T e Vm

»
»
»
Obtenção das isotermas de gás ideal
Segundo termo torna-se negligenciável em temperaturas suficientemente elevadas
Primeiro termo reduz a lei dos gases ideiais a Vm suficientemente elevados
Em ou abaixo da Tc

»
»
Líquidos e gases coexistem
Dois termos entram no balanço em magnitude e oscilações ocorrem

»
Primeiro termo é repulsivo , segundo termo é atrativo
Em Tc, nós deveriamos ter um ponto de inflexão plana, ex, na primeira e segunda
equações de w.r.t Vm = 0
» Resolvendo estas equações para p,Vm e T temos pc,Vc
e Tc nos termos de a e b
 RT
a 
d


Dica: vocdeve usar a eq. original para fazer isto
dp
V  b V 
RT
2a



0
pc= a/27b3, Vc pc= 3b e Tc = 8a/27Rb
dV
dV
V  b  V
 Factor de compressibilidade crítico, Zc, pode ser


calculado usando a definição para Z:
RT
2a

d 


 V  b
pVm = RTZ
p V  a 
27Rb  3
 V 
dp
 

2RT
6a
Z





3b






0
27b 
 R8a  8
RT
dV
dV
V

b
V


2
m
m
2
m
m
m
2
2
m
3
m
3
c
m
3
m
m
m
c
2
4
c
m
Esta deveria ser uma constante para todos os gases
e está na Tabela 1.4
Justificativas Feitas no quadro
3. O príncipio dos estados correspondentes
(Comparando diferentes gases)

Diferentes gases tem
diferentes valores de p,
V e T no seus pontos
críticos.
p (atm)

Você pode compará-los
a qualquer valor pela
criação de uma variável
reduzida obtida pela sua
divisão por um valor
crítico correspondente.
pr
3. O príncipio dos estados correspondentes
(Comparando diferentes gases)
»
»
»
»
preduzida = pr = p / pc;
Vreduzido = Vr = Vm / Vc;
Treduzida = Tr = T/ Tc
Isso coloca todos os gases na
mesma escala e eles se
comportam de forma regular;
gases com o mesmo volume e
temperatura reduzidos
exercem a mesma pressão
reduzida
 Lei dos estados
correspondentes
 Independentes das
equações de estado tendo
duas variáveis.
p (atm)
pr
3. O príncipio dos estados correspondentes
(Comparando diferentes gases)

O princípio dos estados correspondentes é somente uma aproximação do
comportamento real, mais exata para gases com moléculas esféricas.
Ela falha, e ás vezes muito, quando as moléculas do gás não são esféricas
ou são polares.
A equação de van der Waals em termos das variáveis reduzidas

Temos:

Esta equação tem a mesma forma que a equação original,
mas os coeficientes a e b, que caracterizam cada gás,
desapareceram da expressão.
Justificativas feitas no quadro

