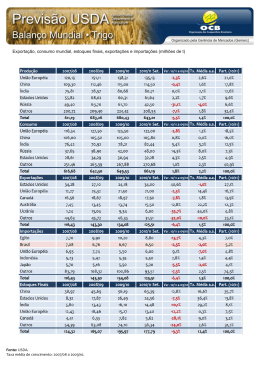
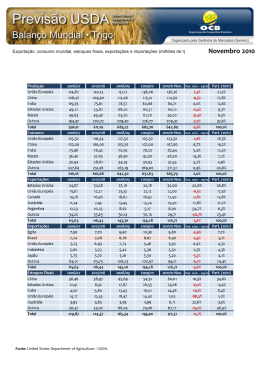
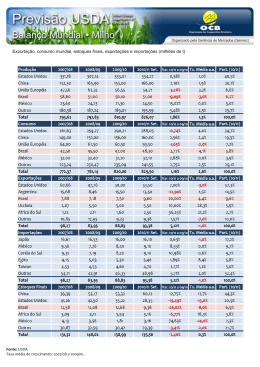
Lista de exercícios: Polinômios – Problemas Gerais – Prof ºFernandinho
Questões:
01.(GV) Num polinômio do terceiro grau, o coeficiente de é 1. Sabendo-se que 0 4, 1 6 e
2 18, calcule o valor de 1.
02.(GV) Dado o polinômio 2 5 3 2 5 1, calcule o
valor de sabendo-se que o polinômio P(x) é identicamente nulo.
03.(MP) Dado o polinômio 2 . 1, onde ∈ . Se 2 3. 0, calcule .
04.(MP) Determinar de modo que 3. 2 . 4 ≡ 2 4.
05.(MAUÁ) Determinar os valores de a, b e c na identidade: 1 ≡ . 1 . 06.(PUC) Sendo 1 1. para todo valor real de x, quanto vale a + b ?
!
07.(MP) Calcule o valor de para que se tenha !.!
"
≡!!
#
, para todo x real, com $ 0 $ 5.
08.(PUC) Calcule os valores de , &ara que o polinômio 2 2 7 5 2 e o
polinômio ( & ) 1 & & sejam idênticos.
09.(FUVEST) Um polinômio , de terceiro grau, satisfaz as seguintes condições:
1 0 e ≡ . Determine o valor de P(2).
10.(MP) Obtenha o quociente e o resto da divisão de 2 1 por ( 2 pelo
método da chave.
11.(MP) Obtenha o quociente e o resto da divisão de ) 3 1 por ( 1 pelo
método de Descartes (ou dos coeficientes a determinar).
12.(GV) Dividindo o polinômio P(x) por 1 obtém-se quociente igual a x – 5 e resto igual a 13x + 5.
Calcule o valor de P(1).
13.(MP) Se o polinômio com a e b reais é divisível por ( 3 1, quanto vale
a soma S = a + b ?
14.(MACK) Calcule reais positivos de modo que ) 1 seja divisível por . .
15.(ITA) Quais são os valores de a, b e c que tornam o polinômio 4 2 ) 2 divisível pelo polinômio ( 2 2 1 ?
16.(GV) Sendo 4 * 2 2 ) , e + 2 2 1, determine os
valores de a, b e c que tornam P(x) divisível por G(x).
17.(ITA) Sejam a, b, c e d constantes reais. Sabendo que a divisão do polinômio , ) pelo
polinômio - 2 4 é exata, e que a divisão do polinômio . / 3 pelo
polinômio 0 2 tem resto – 5, determine o valor de a + b + c + d.
18.(MP) Determinar no polinômio 1 sabendo que P(1) = 3 e que P(x) é
divisível por x – 2.
19.(MP) Sendo &um número natural qualquer, qual é o resto de divisão de 5 1 4 12 2 por x + 1 ?
20.(ITA) A divisão de um polinômio P(x) por resulta no quociente 6 5 3 e resto 7. Qual é o
resto da divisão de P(x) por 2 1 ?
21.(GV) Qual é o resto da divisão de 3 4 5 6 * ) 1 pelo
binômio 1 ?
22.(MP) Determine "" de modo que . 6. 8 seja divisível por .
23.(GV) Dividindo o binômio 33 1 pelo binômio 0 1, obtemos como resto o binômio
8 . Determine os coeficientes a e b do binômio R(x).
24.(ITA) A divisão de um polinômio P(x) por (x – 1).(x – 2) tem resto x +1. Se os restos das divisões de P(x)
por x – 1 e x – 2 são, respectivamente, os números a e b, calcule o valor .
25.(MACK) Um polinômio P(x), de grau maior que 1, deixa resto 1, quando dividido por x – 2, e deixa resto 2,
quando dividido por x – 3. Qual é o resto da divisão de P(x) por 5 6 ?
26.(MAUÁ) Determinar p e q de modo que o polinômio 2 3 2 seja
divisível por x e por x – 2.
27.(MACK) O polinômio é divisível por x – 1 e por x + 1. Quando o dividimos por
x – 2, obtemos resto igual a 12. Nessas condições, calcule o valor de a, b e c.
28.(FUVEST) Um polinômio P(x) é divisível por 1 e, dividido por 1, dá quociente 4 e o resto
R(x). Se R(2) = 9, determine P(x).
29.(ITA) Dividindo-se o polinômio ) 1 por x – 1, obtém-se resto igual a 2. Ao
".#
dividir P(x) por 1, obtém-se resto igual a 3. Sabendo que P(x) é divisível por x – 2, calcule o valor de .
9
30.(FUVEST) O polinômio , em que a e b são números reais, tem restos 2 e 4 quando
dividido por x – 2 e x – 1, respectivamente. Nessas condições determine o valor de a e b.
31.(MACK) Um polinômio P(x) dividido por 2 tem resto 2 1. Qual é o resto da divisão do
polinômio P(x) por 1 ?
32.(UNESP) Considere o polinômio /, onde b, c e d são constantes reais. A derivada
de P(x) é, por definição, o polinômio ( 3 2 . Se (1 0, (1 4 e o resto da divisão de
P(x) por x – 1 é 2, calcule os valores de b, c e d.
33.(ITA) Um polinômio P(x), dividido por x + 1 dá resto – 1, por x – 1dá resto 1 e por x + 2 dá resto 1. Qual
será o resto da divisão do polinômio por (x + 1).(x – 1).(x + 2)?
34.(MP) Um polinômio P(x) dividido por x – 2 dá resto 4. O quociente desta divisão é então dividido por x – 5,
obtendo-se resto 10. Determine o resto da divisão de P(x) por (x – 2).(x – 5) ?
35.(ITA) Um polinômio P(x), dividido pelo binômio x – 1, dá resto 3. O quociente desta divisão é então
dividido pelo binômio x – 2, obtendo-se resto 2. Qual é o resto da divisão de P(x) por (x – 1).(x – 2)?
Gabarito:
01. P(– 1) = 6
02. 9
03. P(m) = – 3
04. a = 5 e b = 3
05. a = 1, b = 0, c = 1
06. a + b = 0
07. a = – 3 e b = 2
08. m = 1, n = 2 e p = – 3
09. P(2) = 6
10.
13. S = – 11
14. p = √2 e q = 1
17. a + b + c + d = 21
18. a = e b = 21. R(x) = 3
22. ±2 ou ±√2
25. R(x) = x – 1
26. e 29.
".#
9
9
33. 8 1
( 2 1
8 3 3
11.
( 4
8 5
12. P(1) = 14
15. a = 3, b = – 2, c = 1
16. a = – 3, b = 3, c = – 1
19. R(x) = 7
20. R(x) = 5
23. a = 3 e b = 1
24. 13
27. a = 2, b = - 1, c = - 2
28. ) 3 3
30. a = – 6 e b = 9
31. R(x) = – 3
32. b = – 1, c = – 1 e d = 3
34. R(x) = 10x – 16
35. R(x) = 2x + 1
4
6
)