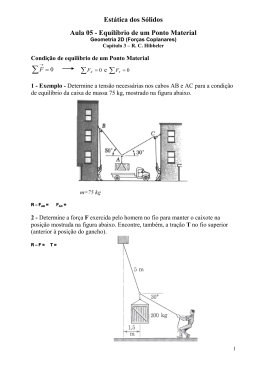
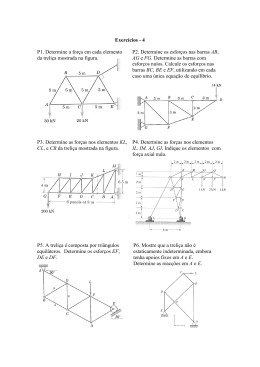
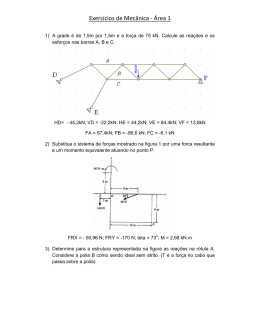
Treliças Planas
Professores:
Nádia Forti
Marco Carnio
TÓPICOS ABORADADOS NETA AULAS
Estudo de treliças planas
Método dos nós
DENOMINAÇÃO DE TRELIÇA PLANA
Denomina-se treliça plana, o conjunto de
elementos de construção (barras redondas,
chatas, cantoneiras, I, U, etc.), interligados
entre si, sob forma geométrica triangular,
através de pinos, soldas, rebites, parafusos,
que visam formar uma estrutura rígida, com a
finalidade de resistir a esforços normais
apenas.
TRELIÇA SIMPLES
A treliça é uma estrutura de elementos
delgados ligados entre si pelas extremidades.
Geralmente os elementos de uma treliça são
de madeira ou de aço e em geral são unidos
por uma placa de reforço com mostrado na
figura.
TRELIÇAS PLANAS
As treliças planas são aquelas que se
distribuem em um plano e geralmente são
utilizadas em estruturas de telhados e
pontes.
TRELIÇA DE UMA PONTE
PROJETO DE TRELIÇA
Hipóteses:
1. As ligações entre elementos são geralmente
formadas pelo aparafusamento ou soldagem de
suas extremidades em uma placa de ligação, ou
ainda simplesmente atravessando cada um dos
elementos com um parafuso. Estas ligações são
chamadas NÓS;
2. Todas as cargas são aplicadas aos nós,
normalmente o peso próprio é desprezado pois a
carga suportada é bem maior que o peso do
elemento.
PROJETO DE TRELIÇA
Os elementos são geralmente de madeira ou perfis
metálicos;
4. Os elementos são unidos nos NÓS através de
pinos lisos (o giro é livre). Esta hipótese é
satisfatória desde que os eixos geométricos dos
elementos sejam concorrentes;
5. As treliças planas são montadas a partir da
combinação de geometrias triangulares, ou seja a
forma mais simples de uma treliça é um triângulo.
3.
ELEMENTOS DE DUAS FORÇAS
Devido as hipóteses simplificadoras, os elementos
de uma treliça atuam como barras de duas forças.
Se uma força tende a alongar o
elemento, é chamada de força de
tração.
Se uma força tende a encurtar o
elemento, é chamada de força de
compressão.
MÉTODO DOS NÓS
A análise é realizada a partir do diagrama de corpo
livre de cada nó que compõe a treliça.
São válidas as equações de equilíbrio da estática.
CONSIDERAÇÕES
Convenção de sinais
Admitir inicialmente que todas as barras são
tracionadas
Nó
- Saindo do nó: Tração
- Entrando no nó: Compressão
Barra
Nó
EXEMPLO
E
F
9tf
3m
A
D
B
C
9tf
3m
3m
3m
PASSO A PASSO
10 Passo : Obtenção de todo o carregamento
externo sobre a treliça, assim, deve-se calcular,
inicialmente, as reações dos apoios.
PASSO A PASSO
20 Passo: Diagrama do corpo livre para cada parte
componente da treliça (nós e barras) para a análise
de cada nó. Admitindo-se que as barras estejam
F
F
tracionadas.
E
F
EF
FE
9tf
FEA
FFB
FFD
FEB
FFC
FAE
FBF
FBE
FCF
FDF
A
D
9tf
FAB
6tf
FBA
B
FBC
FCB
C
FCD
9tf
FDC
3tf
PASSO A PASSO
30 Passo: Desmembramento da treliça,
considerando o equilíbrio de cada nó componente da
treliça, começando-se por um nó, no qual se tenha
no máximo duas incógnitas.
Y
X =4,24
FAE
A
3m
FAEY
9tf
FAB
6tf
FAE
θ
X
FAEX
3m
EXERCÍCIO Determine as forças normais que atuam nas barras
da treliça mostrada na figura e indique se as barras
estão sob tração ou compressão.