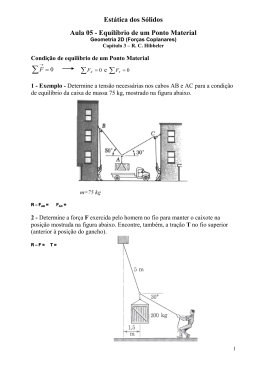
TRELIÇAS

Treliça é uma estrutura de membros esbeltos conectados entre si
em suas extremidades.

Os membros normalmente usados em construções consistem de
escoras de madeira ou barras de metal. A treliça mostrada na
Figura a seguir é um exemplo típico de treliça de telhado.
TRELIÇAS SIMPLES
Como esse peso atua no mesmo plano da treliça, as
análises das forças desenvolvidas nos membros da
treliça serão bidimensionais.
TRELIÇAS SIMPLES
No caso de uma ponte, o peso no tabuleiro é primeiro
transmitido para as longarinas, depois para as vigas de
piso e, finalmente, para os nós das duas treliças laterais.
TRELIÇAS SIMPLES
Assim como no telhado, o peso da ponte de treliça também é
coplanar.
TRELIÇA SIMPLES
Se os três membros são conectados por pino em suas
extremidades, eles formam uma treliça triangular que
será rígida.
TRELIÇA SIMPLES
Unir dois ou mais membros e conectá-los a um novo nó
D forma uma treliça maior.
 Para
determinar os esforços internos nas barras
das treliças plana, devemos verificar a condição
de Isostática da Treliça, sendo o primeiro passo.
 Depois calculamos as reações de apoio e os
esforços normais axiais nos nós. Tais esforços
serão denominados de N.
n = nº de nós
b = quantidade de barras
ѵ = nº de reações (Verticais e Horizontais)

Condição de Treliça Isostática:
2.n=b+ѵ
 2º
Calcular as Reações de Apoio (Vertical e
Horizontal):
ΣFx = 0
ΣFy = 0
ΣM = 0
 Por
convenção usaremos:
(–)

no sentido horário →

no sentido anti-horário →
(+)
O MÉTODO DOS NÓS
Por exemplo, três forças atuam sobre o pino, a saber, a
força de 500 N e as forças exercidas pelos membros BA
e BC.
CALCULE AS REAÇÕES DE APOIO E AS FORÇAS
NORMAIS NAS BARRAS
CALCULE AS REAÇÕES DE APOIO E AS FORÇAS
NORMAIS NAS BARRAS
BIBLIOGRAFIA
 BEER,
F. P.; JOHNSTON JR, E. R.;
EISENBERG, E. R. Mecânica vetorial para
engenheiros: estática. 7.ed. SP: McGraw
Hill - Artmed, 2006.
 CRAIG JR, R. R. Mecânica dos materiais.
2. ed. RJ: LTC, 2002.
 HIBBELER, R. C. Estática: mecânica para
engenharia. v.1. 12. ed. SP: Pearson, 2011.