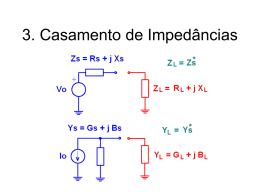
Laboratório de Circuitos 2
Prof. Joaquim Rangel Codeço
Transformação de impedância.
Um circuito muito usado em frequências acima das de aúdio, normalmente chamado de acoplador
de impedância, baseia-se no fato que uma resistência Rs em série com uma reatância Xs (indutiva
ou capacitiva ) tem sua impedância igual a uma resistência Rp em paralelo como uma reatância Xp
(do mesmo tipo da série).
Circuito série
Circuito paralelo
2
Rp
Rs
1
Xs
Xp
1
2
Isto é somente verdade se mantivermos a frequência constante. (*).Como a impedância dos
circuitos são iguais, seus fatores de qualidade também o são, portanto podemos deduzir que:
=
portanto, (1)
, do exposto vemos que
e portanto temos um meio de modificarmos impedâncias para frequências fixas, usando a
transformação série-paralelo quando quisermos aumentar a impedância e a transformação paralelosérie quando quisermos diminuir, e ainda com o uso da ressonância, podemos deixar a impedância
puramente resistiva. Observamos que as grandezas de Xs e Xp será sempre do mesmo tipo, ou seja
se uma é capacitiva a outra também é.
Exemplo. Suponha que queiramos transformar a resistência de 10Ω em 50Ω na frequência de
1MHz. Verificamos primeiramente que teremos que transformar um circuito série em paralelo, pois
este é o modo de aumentarmos a impedância e
, Portanto Q =2 sendo Xs=QsRs
logo Xs= 20Ω que pode ser indutivo ou capacitivo. Escolhamos um indutor, por exemplo:
= 3,18 µH. Este circuito tem como equivalente na frequência dada, uma resistência paralela de
50Ω com uma reatância indutiva paralela de Xp =20(1+1/22)=25Ω, portanto
(*)Análise de Circuitos em Engenharia (Willian H. Hayt, Jr. e Jack E. Kemmerly) Editora McGraw do Brasil LTDA ,14.4 pag.395
(Transformação de Impedância , Prof. Joaquim Rangel Codeço)
Observamos então que dos 10Ω iniciais, transformamos em 50Ω em paralelo com uma reatância
indutiva de j25Ω. Se quisermos deixar o circuito puramente resistivo de 50Ω adicionaremos em
paralelo, uma reatância de sinal contrário também de -j25Ω o que significa colocar um capacitor
de
≈ 6,4nF
que na frequência de 1 MHz, estará ressonante com o indutor.
Todo processo é representado abaixo.
Observe que este mesmo circuito que está transformando 10Ω em 50Ω na frequência de 1Mhz é o
mesmo que transforma 50Ω em 10Ω se considerarmos a transformação inversa colocando 50Ω na
saída onde tínhamos a conversão para 50Ω, teremos na outra ponta, 10Ω. Lembramos que
poderíamos ter escolhido inicialmente a reatância série capacitiva e a paralela de indutiva com os
mesmos valores de reatância.
Preparatório para a parte prática. (Transformação de Impedância , Prof. Joaquim Rangel Codeço)
Aluno:____________________________________________________
1) Calcule um circuito que transforme 47 Ω para um valor maior, puramente resistivo na
frequência de 100kHz, usando um indutor de 680µH e considere que a resistência interna do
indutor é 8Ω.
a) Calcule Qs considerando Rs= 47+8 Ω Q=_______________________
b) Calcule Rp considerando o Rs acima Rp=________________________
c) Calcule Xp = _____________________
d) Calcule o Capacitor com C =
= ____________________
e) Considere o capacitor comercial mais próximo do encontrado e recalcule a frequência de
ressonância considerando que Xp não mude com o novo valor de frequência.
Observe que os valores comerciais de C são dados pelos valores
(1.2;1.5;2.2;2.7;3.3;3.9;4.7)
C =______________
fo=_____________
f) Para este novo valor de f, recalcule Xs, Q, Rp
Xs=______________
Q= ______________
Rp=______________
(Transformação de Impedância , Prof. Joaquim Rangel Codeço)
Relatório do Experimento de Transformação de Impedâncias
Alunos: 1 ___________________________________________________________
2 ___________________________________________________________
1) Meça a resistência do indutor RL=__________________________
2) Montando o circuito acima com o capacitor encontrado no preparatório, obtenha a
frequência ressonância através da fase. fo =__________________
3) Encontre Rp Calculando V/I -100Ω=____________________
4) Com o novo valor de fo, recalcule Rp. Compare com o valor acima.________________
5) Monte o circuito abaixo ajustando o potenciômetro para o valor do item 2.
6)
7)
8)
9)
Verifique a ressonância que teoricamente não deveria ter mudado, fo=________________
Obtenha o Rin, Achando V/I – 47Ω na ressonância= Rin____________________
Obtenha Rs subtraindo de Rin, o Rl = ________________________
Comente os resultados e validade deles.
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________