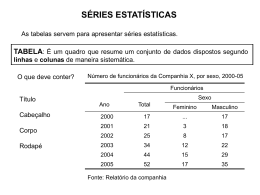
Séries Estatísticas
FAPAN - Faculdade de Agronegócio
de Paraíso do Norte
Disciplina: Estatística Aplicada
Tabelas
• É um quadro que resume um conjunto de observações
• Compõe-se de:
– Corpo
– Cabeçalho
– Coluna Indicatória
– Linhas
– Casa ou célula
– Título
Ainda há os elementos complementares da tabela (colocadas no
rodapé):
• Fontes
• Notas
• Chamadas
Tabela
Tabela
Séries Estatísticas
• Séries históricas, cronológicas, temporais ou
marchas.
Séries Estatísticas
• Séries históricas, cronológicas, temporais ou
marchas.
Séries Estatísticas
• Séries históricas, cronológicas, temporais ou
marchas.
Séries Estatísticas
• Séries geográfica, espaciais, territoriais ou de
localização
Séries Estatísticas
• Séries geográfica, espaciais, territoriais ou de
localização
Séries Estatísticas
• Séries geográfica, espaciais, territoriais ou de
localização
Séries Estatísticas
• Séries específicas ou categóricas
Séries Estatísticas
• Séries específicas ou categóricas
Séries Estatísticas
• Séries específicas ou categóricas
Séries Estatísticas
• Séries conjugadas ou de dupla entrada
Séries Estatísticas
• Séries conjugadas ou de dupla entrada
Distribuição de Frequência
• Dados Absolutos: são dados estatísticos
resultantes da coleta direta da fonte, sem
outra manipulação, senão contagem ou
medida.
• Dados Relativos: são os resultados de
comparações por quociente (razões) que se
estabelecem entre os dados absolutos e tem
por finalidade realçar ou facilitar as
comparações entre quantidade.
Distribuição de Frequência
• Tabela primitiva
Distribuição de Frequência
• Rol
Distribuição de Frequência
• Distribuição de Frequência
Distribuição de Frequência
• Distribuição de Frequência com intervalos de
classe
Distribuição de Frequência
• Distribuição de Frequência com intervalos de
classe
Distribuição de Frequência
• Classe de Frequência (i): são intervalos de
variação da variável (k = nº total de classes):
154 |― 158  i = 2
• Limites de Classe: são os extremos de cada
classe:
ℓ2 = 154 e L2 = 158
• Amplitude de um Intervalo de Classes (h): é a
medida do intervalo que define a classe:
hi = Li – ℓi
h2 = L2 – ℓ2  158 – 154 = 4  h2 = 4 cm
Distribuição de Frequência
• Amplitude total da distribuição (AT): é a
diferença entre o limite superior da última
classe e o limite inferior da primeira classe:
AT = limite superior máximo – limite inferior máximo
AT = 174 – 150 = 24  AT = 24 cm
• Amplitude amostral (AA): é a diferença entre
o valor máximo e o valor mínimo da amostra:
AA = x(máximo) – x(mínimo)
AA = 173 – 150 = 23  AA = 23 cm
Distribuição de Frequência
• Ponto médio de uma classe (xi): é o ponto
que divide o intervalo de classe em duas
partes iguais:
xi 
i  Li
2
x2 
2  L2
2
 x2 
154  158
2
 156  x 2  156
Tipos de Frequência
• Frequência simples ou absoluta (fi): é o nº de
observações correspondentes a essa classe:
f1= 4, f2= 9, f3= 11, f4= 8, f5= 5 e f6= 3
A soma de todas as frequências é dado por:
k
k
É evidente que:
temos:
 fi  n

i 1
fi
i 1
6

i 1
f i  40
ou:

f i  40
Tipos de Frequência
Tipos de Frequência
• Frequência relativas (fri): são os valores das
razões entre as frequências simples e a
frequência total:
fi
fr i 

fi
Logo, a frequência relativa da terceira classe é:
fr 3 
f
3

f
 fr 3 
3
11
40
 0 , 275  fr 3  0 , 275
Tipos de Frequência
• Frequência acumulada (Fi): é o total das
frequências de todos os valores inferiores ao
limite superior do intervalo de uma dada
classe:
Fk 

fi
(i = 1, 2, ..., k)
Logo, a frequência acumulada até a terceira classe é:
3
F3

i 1
fi  f 1  f
2 
f 3  F 3  4  9  11  F 3  24
Tipos de Frequência
• Frequência acumulada relativa (Fri): é a
frequência acumulada da classe, dividida pela
frequência total da distribuição:
Fr i 
Fi

fi
Logo, a frequência acumulada até a terceira classe é:
Fr 3 
F3

f
 Fr 3 
3
24
40
 0 , 600  Fr 3  0 , 600
Tipos de Frequência
Distribuição de frequência sem
intervalos de classe
• Isso acontece quando se trata de uma variável
discreta de variação relativamente pequena.
Distribuição de frequência sem
intervalos de classe
• Seja x a variável “nº de cômodos das casas
ocupadas por 20 famílias entrevistadas”
Distribuição de frequência sem
intervalos de classe
• Completada com vários tipos de frequência:
Número de classes – Intervalos de
classe
• Para a determinação do nº de classes
podemos usar a regra de Sturges:
Número de classes – Intervalos de
classe
• Para a determinação do nº da amplitude do
intervalo de classe:
h
AT
i
Logo, para o exemplo anterior:
h
173  150
6

23
6
 3 ,8  h  4