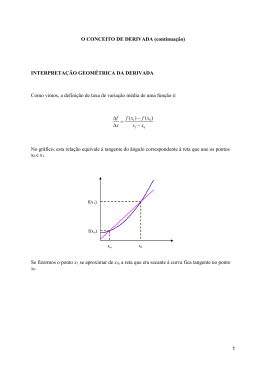
Elementos de Cálculo Diferencial
Na aula anterior vimos a noção de derivada de uma
função.
Suponha que uma variável y seja dada como uma função f
de uma outra variável x,
y = f ( x ).
Por exemplo, a variável y pode ser o tamanho de uma
população e a variável x pode ser o tempo; ou y pode ser a
concentração de uma enzima e x é novamente o tempo.
Nem sempre a variável independente x é o tempo. Por
exemplo, ela pode ser a temperatura de um dado ambiente
ou a distância medida a partir de um ponto de referência.
Sem nos importarmos com o que y e x representam
biologicamente ou fisicamente, podemos pensar nelas e na
função f como entidades matemáticas.
Se representarmos a função y = f(x) em um gráfico,
podemos definir a taxa de variação de y quando x varia
de x1 para x2 como,
∆y y 2 − y1 f ( x 2 ) − f ( x1 )
=
=
.
∆x x2 − x1
x 2 − x1
Veja a figura a seguir, reproduzida da aula anterior, só que
agora escrita em termos de y e x.
Da figura, vemos que a taxa de variação ∆y ∆x é igual à
inclinação da reta R que une os pontos (y2,x2) e (y1,x1),
definida por tg θ.
A idéia central do cálculo diferencial está em passar dessa
taxa de variação – que requer o conhecimento do valor da
função em dois pontos – para a taxa de variação
instantânea, calculada em um dado ponto x da função.
Veja o gráfico a seguir, também retirado da aula anterior,
só que escrito em termos das variáveis x e y.
Do desenho vemos que, à medida que ∆x → 0, a reta R
tende para a reta tangente à curva y(x) no ponto x1.
A inclinação da reta tangente à função y(x) no ponto x1 é
chamada de derivada de y em relação a x no ponto x1,
dy
dx
x1
∆y
= lim
.
x2 → x1 ∆x
Quando o limite definido pela equação acima existe
(existem casos em que ele não existe), dizemos que a
função y = f(x) é diferenciável em x = x1.
Existem diversas maneiras simbólicas diferentes de se
denotar a derivada de uma função. Dependendo do livro
que você venha a consultar você poderá ver uma ou outra,
mas todas são equivalentes. As mais comuns são: y’(lê-se
y linha), f’(x1), df/dx.
Também é muito comum se representar a derivada de uma
função que depende do tempo y(t) em relação a t por um
•
ponto acima da função: y (lê-se y ponto).
Até aqui, o que vimos é o que já havia sido apresentado na
aula anterior. A derivada de uma função y = f(x) em um
dado ponto x1 é igual à inclinação da reta tangente à
função f no ponto x1 (calculada como tg θ, onde θ é o
ângulo feito pela reta tangente com a horizontal).
Essa definição – que é a visão geométrica da derivada – é
muito útil quando se tem condições de desenhar o gráfico
da função f(x). Mas nem sempre isso é possível, ou
desejável, como no caso do item (b) do exercício 5 da aula
10. Em tais casos, é desejável poder calcular o valor da
derivada analiticamente ao invés de geometricamente.
Para fazermos o cálculo analítico de uma derivada, temos
que usar a definição,
dy
dx
x1
∆y
= lim
.
x2 → x1 ∆x
Portanto, temos que ser capazes de calcular o limite
acima.
Para entender como isso pode ser feito, é mais fácil
reescrever a definição substituindo x1 por x e x2 por h.
Neste caso, ∆x = h (veja a figura abaixo).
Chamamos h de incremento em x. Ele pode ser positivo
(isto é, estar à direita de x), ou negativo (isto é, estar à
esquerda de x). O valor de y = f(x) no ponto x + h é igual a
f(x + h), de maneira que ∆y = f(x + h) − f(x).
Então, podemos escrever,
∆y f ( x + h ) − f ( x )
=
,
∆x
h
e a derivada de y = f(x) no ponto x fica sendo dada por,
dy
f (x + h ) − f (x )
= f ' ( x) = lim
.
h
→
0
dx
h
O número obtido a partir da equação acima é igual à
inclinação da reta tangente à função y = f(x) no ponto x.
Para se calcular o limite acima, deve-se manter a variável
x constante, mas fazer h ir para zero. Porém, não se pode
fazer isso diretamente na equação acima, pois fazendo h =
0 nela obtemos,
f (x + 0) − f ( x) f ( x) − f ( x) 0
= ,
=
0
0
0
e isso não tem significado.
Na realidade, nem sempre é fácil calcular o limite acima e
um pouco de engenhosidade matemática é necessário.
Vamos mostrar alguns exemplos de cálculos de derivadas
para funções em que esse cálculo não é muito difícil.
Depois, vamos apenas dar os resultados do cálculo da
derivada para outras funções mais complicadas.
Exemplo 1. Calcule a derivada da função y = f ( x) = ax + b ,
onde a e b são constantes, em um ponto x qualquer.
Para calcular a derivada, precisamos primeiro calcular,
f ( x + h) − f ( x ) [ a ( x + h) + b] − ( ax + b) ah
=
=
= a.
h
h
h
Então,
dy
f ( x + h) − f ( x )
= f ' ( x ) = lim
= lim a = a.
h →0
h →0
dx
h
Portanto, a derivada de uma função linear cujo coeficiente
angular é a é igual ao próprio coeficiente angular a. Note
que isso faz sentido, de acordo com a interpretação
geométrica da derivada, pois a reta tangente à função
linear é a própria função e a sua inclinação é dada pelo seu
coeficiente angular.
Este exemplo nos permite deduzir um caso particular, que
é o da derivada de uma função constante, y = f ( x) = b.
Exemplo 1’. Calcule a derivada da função y = f ( x) = b ,
onde b é uma constante, em um ponto x qualquer.
0
f ( x + h) − f ( x )
dy
= f ' ( x ) = lim
= lim = 0.
h →0
h →0 h
h
dx
Uma função constante y = b é uma reta paralela ao eixo-x;
portanto, o seu coeficiente angular (a sua inclinação) é
nulo. É por isso que a sua derivada é zero.
Exemplo 2. Calcule a derivada da função quadrática
y = f ( x) = x 2
em um ponto x qualquer.
Para calcular a derivada, precisamos primeiro calcular,
f ( x + h) − f ( x) ( x + h) 2 − x 2 x 2 + 2hx + h 2 − x 2 2hx + h 2
=
=
=
= 2 x + h.
h
h
h
h
Então,
dy
= f ' ( x ) = lim(2 x + h ) = 2 x.
h →0
dx
Portanto, a derivada de uma função quadrática, y = x2,
num dado ponto x é igual a 2 vezes esse valor de x.
Este caso é interessante, porque mostra que a derivada de
uma função f(x) pode ser, ela mesma, uma função de x.
No caso, a derivada da função quadrática y = x2 é a função
linear g = 2x.
A partir da fórmula acima, podemos calcular a derivada da
função y = x2 em alguns pontos, por exemplo: x = 0, x =
±1 e x = ±2.
Em x = 0: y’(0) = 2.0 = 0.
Em x = 1: y’(1) = 2.1 = 2.
Em x = −1: y’(−1) = 2.(−1) = −2.
Em x = 2: y’(2) = 2.2 = 4.
Em x = −2: y’(−2) = 2.(−2) = −4.
Essas derivadas podem ser vistas geometricamente no
gráfico da função y = x2 dado a seguir. O gráfico mostra as
retas tangentes à função nos pontos x = ±1 e x = ±2. A reta
tangente à função y = x2 no ponto x = 0 é o próprio eixo-x.
Note que quanto mais distante x fica da origem, mais
inclinada fica a curva.
Do lado direito da origem, temos inclinações positivas e,
do lado esquerdo, temos inclinações negativas.
O gráfico abaixo mostra a função derivada de y = x2, g(x)
= 2x.
Note que a derivada é positiva para x > 0 e é negativa para
x < 0. Em x = 0, a derivada é nula.
Exemplo 3. Calcule a derivada da função cúbica
y = f ( x) = x 3
em um ponto x qualquer.
Para calcular a derivada, precisamos primeiro calcular,
f ( x + h) − f ( x) ( x + h) 3 − x 3 ( x + h )( x 2 + 2hx + h 2 ) − x 3
=
=
=
h
h
h
x 3 + 3hx 2 + 3h 2 x + h 3 − x 3 3hx 2 + 3h 2 x + h 3
=
=
= 3 x 2 + 3hx + h 2 .
h
h
Então,
(
)
dy
= f ' ( x ) = lim 3 x 2 + 3hx + h 2 = 3 x 2 .
h →0
dx
Portanto, a derivada de uma função cúbica, y = x3, num
dado ponto x é igual a 3 vezes esse valor de x ao
quadrado.
Exemplo 4. Calcule a derivada da função potência
y = f ( x) = x n
em um ponto x qualquer, para n sendo um
número real qualquer, positivo ou negativo.
Este é um exemplo de uma função cuja derivada não é tão
fácil de ser calculada.
No entanto, existem métodos que nos permitem obter o
resultado. Eles não serão dados aqui, o que nos importa
em biologia é saber o resultado.
Se y = f(x) = xn, onde n é um número real qualquer, inteiro
ou fracionário, positivo ou negativo, então a derivada de y
em qualquer ponto x é,
dy
= f ' ( x) = nx n−1.
dx
Esta é uma fórmula tão importante que é melhor você
memorizá-la. Para ajudar, vamos calcular as seguintes
derivadas como exercício:
y = x5. y’(x) = 5x4.
y = x-7. y’(x) = −7x-8 = −7/x8.
y = x-1. y’(x) = −x-2 = −1/x2.
1
y = x1/2. y’(x) = 2 x
1/3
’
y = x . y (x) =
−1
2
=
1
2 x
.
1 −23
1
x
= 2 ..
3
3x 3
Nem toda função possui derivada em todos os pontos x do
seu domínio. Vejamos o seguinte caso.
Exemplo 5. Calcule a derivada da função módulo
y = f ( x) = x
no ponto x = 0.
Um fato que não foi mencionado anteriormente, porque
não foi necessário, é que o limite de uma função quando o
incremento ∆x = h → 0 pela direita de x pode ter um valor
diferente do limite da função quando ∆x = h → 0 pela
esquerda de x.
No caso da função módulo, quando h → 0 pela direita de x
= 0:
lim
h →0
h >0
h
0+h − 0
f ( 0 + h ) − f ( 0)
h
= lim
= lim = lim = 1.
h →0
h →0 h
h →0 h
h
h
h >0
h >0
h >0
Já quando h → 0 pela esquerda de x = 0:
lim
h →0
h <0
h
0+h − 0
f ( 0 + h ) − f ( 0)
−h
= lim
= lim = lim
= −1 .
h →0
h →0 h
h →0 h
h
h
h<0
h<0
h <0
Para que a derivada da função y = x em x = 0 existisse,
seria
necessário
que
o
limite
fosse
único,
independentemente de como nos aproximamos de x = 0,
pela direita ou pela esquerda. Porém, neste caso isso não
acontece: quando nos aproximamos pela direita, o limite
vale +1; quando nos aproximamos pela esquerda, o limite
vale −1. Portanto, a função y = x não possui derivada em
x = 0.
O gráfico da função módulo está dado abaixo.
Observe que, na origem, o gráfico de
y= x
forma um
“bico”. Em um caso assim, não se pode determinar a
tangente à curva no ponto do “bico” (x = 0). Portanto, a
função não possui derivada nesse ponto.
Note que a derivada da função módulo existe para
qualquer outro ponto x ≠ 0. Nesses pontos, a função
módulo é uma função linear (linha reta) e a sua derivada
(veja o exercício 1) é uma constante igual ao coeficiente
angular da reta, que nesse caso é +1 para x > 0 e x = −1
para x < 0.
Portanto, a derivada de
y= x
é uma função descontínua na
origem. Ela vale +1 à direita de x = 0 e vale −1 à
esquerda de x = 0, pulando bruscamente de um valor para
outro quando cruzamos o ponto x = 0.
Veja o gráfico da derivada de
y= x
dado abaixo.
Compare este gráfico com o gráfico da derivada da função
y = x2, g(x) = 2x, dado algumas páginas acima. Note que a
derivada de y = x2 também muda de sinal quando x passa
pela origem, mas essa mudança não é abrupta. Ele é
descrita por uma função contínua, g(x) = 2x. E a derivada
de y = x2 existe em x = 0. Ela vale f ´(0) = 2.0 = 0.
Quando a derivada de uma função y = f(x) existe em todos
os pontos do seu domínio x, isto é, quando a derivada
varia continuamente de um ponto x para outro, dizemos
que a função y = f(x) é suave.
Quando a derivada de uma função y = f(x) não existe em
um dado ponto x, isto é, quando a função derivada é
descontínua no ponto x, dizemos que a função y = f(x) não
é suave em x. Em geral, isso pode ser detectado
visualmente observando o gráfico de y = f(x). Se ele tiver
um “bico” em algum ponto x, ele não terá derivada nesse
ponto.
Existe um outro caso em que uma função y = f(x) não
possui derivada em um dado ponto x. É o caso em que a
própria função y = f(x) é descontínua no ponto x. Veja a
figura abaixo, que mostra uma função contínua em todos
os pontos (gráfico da esquerda) e uma função descontínua
em um ponto x = x2 (gráfico da direita).
No ponto x = x2 a função mostrada à direita é descontínua
e, portanto, não possui derivada. À esquerda de x = x2, a
derivada da função tem um valor constante; à direita de x
= x2, a derivada tem um outro valor constante, mas
diferente do primeiro. E a transição de um valor para o
outro não é contínua.
O que vimos nestes últimos exemplos pode ser sintetizado
na frase:
Diferenciabilidade
implica
em
continuidade,
mas
continuidade não implica em diferenciabilidade.
Ou seja, se uma função y = f(x) é diferenciável num dado
ponto x, ela necessariamente deve ser contínua nesse
ponto. Um exemplo é a função do gráfico à esquerda na
figura anterior.
Por outro lado, o fato de uma função ser contínua num
dado ponto x não é garantia de que a derivada da função
exista em x. Um exemplo é a função módulo,
y= x
. Ela é
contínua em x = 0, mas não possui derivada nesse ponto.
Em geral, qualquer função que tenha um “bico” em um
dado ponto é contínua no ponto, mas não tem derivada
nele.
Estamos falando sobre funções contínuas sem ter dado
uma definição de continuidade. Não vamos dar uma
definição matematicamente rigorosa aqui, mas apenas
uma que – espera-se – vá ajudá-los a entender a idéia de
continuidade:
Uma função contínua é aquela cujo gráfico pode, em
princípio, ser traçado à mão sem que seja preciso levantar
a ponta da caneta ou lápis do papel.
Vamos agora dar, sem demonstração, as fórmulas para as
derivadas de algumas combinações de funções que serão
encontradas muitas vezes ao longo deste curso e de outros
que vocês fizerem.
Vamos supor que as funções f(x) e g(x) tenham derivadas
conhecidas e iguais, respectivamente, a f ’(x) e g’(x).
a) Derivada de uma constante vezes uma função:
d (c. f ( x) )
df ( x)
=c
.
dx
dx
b) Derivada da soma de duas funções:
d [ f ( x ) + g ( x )] df ( x) dg ( x )
=
+
.
dx
dx
dx
c) Derivada do produto de duas funções:
d [ f ( x).g ( x)] df ( x)
dg ( x)
=
.g ( x) + f ( x).
.
dx
dx
dx
d) Derivada de uma função composta (função de função):
Seja a função composta
y = f ( g ( x)).
Então,
dy df dg
=
. .
dx dg dx
Esta fórmula é conhecida como regra da cadeia.
e) Derivada do quociente de duas funções:
⎤
d ⎡ f ( x)
g ( x)⎥⎦ [ f ' ( x).g ( x) − f ( x).g ' ( x)]
⎢⎣
.
=
dx
( g ( x ) )2
f) Derivadas de funções trigonométricas:
d (sen x)
= cos x.
dx
d (cos x)
= −sen x.
dx
1
d ( tg x)
.
=
cos 2 x
dx
1
d (cotg x)
.
=−
sen 2 x
dx
g) Derivada das funções exponencial e logarítmica (na
base e):
( )
d ex
= ex.
dx
d (ln x ) 1
= .
dx
x