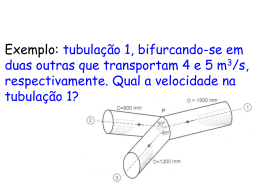
Mecânica dos Fluidos
Aula 03
Prof. Dr. Gilberto Garcia Cortez
1
3.5- Força hidrostática sobre superfícies submersas
A determinação de forças na superfície de corpos submersos é
importante no projeto de tanques para armazenamento de fluidos,
navios, submarinos, barragens e de outras estruturas hidráulicas
que esteja sob ação de forças de superfície submersas.
Para determinar completamente a resultante da força atuando
sobre uma superfície submersa, devemos especificar:
1- A magnitude ou módulo da força resultante;
2- O sentido da força;
3- A linha de ação da força.
3.5.1- Força hidrostática sobre uma superfície plana submersa
A determinação das forças que atuam sobre superfícies planas
submersas é um problema frequente da estática dos fluidos. Essas
forças são devidas às distribuições de pressões nos fluidos, e a força
resultante é obtida através da integração da distribuição de
pressões sobre a superfície plana submersa.
2
a) Superfície plana submersa
A força total de contato superficial no corpo pode ser determinada
pela soma vetorial das forças superficiais em toda a área do corpo
submerso.
g
P0
 (superfície livre)
líquido
dA
FR
dF
y
(+) h
Centro de Pressão, CP
Ponto de aplicação
da força resultante
x’
z
CP
y’
x
y
P
O
x
3
A força de pressão agindo sobre o elemento de área, dA, no ponto O
é dado por:
d F   Pd A (vetor)
dF  PdA (escalar)
(1)
onde o sinal menos indica que a força dF age sobre o elemento de
área dA, em sentido oposto ao da normal da área A. A força
resultante é dado por:


FR  d F   Pd A
(2)
A
A pressão P no ponto O sobre superfície plana de área A é dado por:
P  P0  ρfluidogh
(3)
onde P0 é a pressão na superfície livre (h = 0).
4
Portanto, a força resultante total aplicada a uma superfície plana
submersa horizontal é dado por:
FR 

P0  ρgh d A
(4)
Podemos escrever também:
FR  FRx i  FRy j  FRz k
(5)
onde FRx , FRy e FRz são as componentes escalares de FR nos
sentidos positivos de x, y e z, respectivamente.
5
onde:
FR  FRx i  FRy j  FRz k

F  F .i  d F.i   Pd A.i   PdA
R
x
 Rx

A
Ax


FRy  FR . j  d F. j   Pd A. j   PdA y

A
Ay


FRz  FR .k  d F.k   Pd A.k   PdA z

A
Az









6
b) Superfície plana inclinada
y
dA
h
senθ 
 h  ysenθ
y
7
dA
8
FR 


d F   Pd A
A
FR  
A

P0  ρgh d A
A
h  ysenθ
d A  Wdyk
W = largura da comporta
9
FR
FR



  P0  ρysenθg  Wdyk
  
 

 dA
P
y2


dyk
   P0 W  ρg
Wysenθ



γ

y1 


y
FR
2
2


y
  P0 Wy  ρg
W
senθ  k

2


γ
y1
FR

y 22  y12 
  P0 W  y 2  y1   γ Wsenθ
k





2


A
FR

y 22  y12 
  P0 A  γ Wsenθ
k

2






(6)
10
O momento, M, da força distribuída em relação ao eixo no ponto O
é dado por:
M  r' . FR 
y
FR
z


r . d F   r . Pd A
dF
r'  x' i  y ' j
x
r  xi  yj
x'
CP
y'
o
(7)
d A  dA k
y
x
FR   FR k
11
1
M y  0  x' FR   xPdA  0  x' 
xPdA

FR A
A
1
M x  0  y ' FR   yPdA  0  y ' 
yPdA

FR A
A
(8)
Exemplo 01: A superfície inclinada mostrada, articulada ao longo de
A, tem 5 m de largura. Determine a força resultante, FR , da água e
do ar sobre a superfície inclinada.
12
Solução: Para determinar o vetor FR , devemos especificar:
a) Sua magnitude;
Dados:
b) Seu sentido;
W = 5m (largura da comporta)
c) Sua linha de ação.

= 999kg/m3
água
Patm ( 0)
+h
h
y
P
H
H
 H  ysen30
y
h  D  H
sen30 
13
Equações básicas:


FR  d F   Pd A
P  Patm  ρ água gh
A
a) Uma vez que estamos interessados na força resultante da água
sobre a comporta, desprezamos Patm ( 0) e obtemos:
P  P atm  ρ água gh  ρ água gh
P  ρ água gD  ysen30
14

FR   ρgD  ysenθ Wdyk
 
P
dA
FR
FR
FR
FR
L


y
  ρgW Dy 
senθ  k
2

0
2

L2 1 
  ρgW DL 
k

2 2

kg
m 

4m 2 1 
  999 3 9,81 2 5m 2mx4m 
k
2 2
m
s

kg m
  588011,4 3 2 m 3 k   588011,4 N k
m s
F R   588,01 kN k
15
b) Os momentos em relação ao eixo x passando pelo ponto A:
M
x
 0
A
16
M
x
P  ρ água gD  ysen30
 0
M x  y ' FR 
dA  Wdy
dF   PdA
 ydF  0
A

1
y ' FR  yPdA  0  y ' 
FR
A
1
y' 
FR
 y[ρ
água
 yPdA
A
gD  ysen30]Wdy
A
L
Wρ água g
y' 
[Dy  y 2sen30]dy
FR 0

17
ρgW  Dy
y' 
FR  2
2
L
y


sen30
3
0
3
ρgW  DL2
L3 1 
y' 


FR  2
3 2 
kg
m
5m
64m 3 
 2m x16m 2
y'  999 3 9,81 2

5
2 
m
s 5,8810 kg/m.s 
2
6 
y'  2,22m
Também considerando os momentos em relação ao eixo y passando
pelo ponto A, temos:
M y  x' FR 

xdF  0
A
x' FR 

A
xPdA  0  x' 
1
FR

A
xPdA
18
Como W é constante e a integração está sendo realizada sobre o
eixo y, temos que:
1
x' 
FR

xPdA
1
x' 
FR

W
PdA
2
A
A
W
x' 
2FR
WF R
W 5m
PdA 


 2,5m
2F R
2
2
A



x'  2,5m
FR
c) A linha de ação da força resultante é paralela ao eixo z,
passando sobre r’, ou seja:
r'  x' i  y' j
r'  2,5i  2,22 j m
19
Exemplo 02: A porta lateral do tanque é articulada na borda inferior.
Uma pressão de 100 lbf/ft2 (manométrica) é aplicada na superfície
livre do líquido. Determine a força Ft necessária para manter a porta
fechada.
Comporta

P = 100 lbf/ft2
L = 3ft
 = 100 lbf/ft3
Articulação (eixo x)
b = 2ft
20
Solução: Aplicando os momentos em relação ao eixo x da
z
articulação, temos:

Ft
P0
h
h (+)
dF
L
h =L - z
o
z
Articulação (eixo x)
x
M
Ft 
Ft 
x
 Ft .L 

Mx ()

zdF  0

Mx ()

1
zdF
L

L

1
1
zPdA 
zP bd
z

L
L
dA
A
0
21
P  P0  ρ fluido gh  P0  γ fluido h
h Lz
P  P0  γ fluido L  z 
L
Ft 

1
zbP0  γ fluido L  z dz
L
0
L
Ft 

b
γb
P0 zdz 
L
L
0
L

Lz  z 2 dz

0
2 L
3 L
 P0 bz 
γb  Lz
z 
Ft  

 


L 2
3 0
 2L  0
2
P0 bL2
γb  LL2
L3 
Ft 

 

2L
L 2
3
22
2
P0 bL
P
bL
1
1
γbL
Ft 
 γ bL2     0

2
2
6
 2 3
lbf 2ft x 3ft
lbf 2 ft x 9 ft 2
Ft  100 2 x
 100 3 x
2
6
ft
ft
Ft  600 lbf
Este problema ilustrou:
a) A inclusão da pressão manométrica diferente de zero na
superfície livre do líquido;
b) O emprego direto do momento distribuído sem a avaliação da
força resultante e sua linha de ação em separado.
23
Exemplo 03: A medida que a água sobe no lado esquerdo da
comporta retangular de largura W, ela abrir-se-á automaticamente.
A que profundidade ‘D’ acima da articulação (A) isso ocorrerá?
Despreze a massa da comporta.
y

h1
D
P1
h2
1,5 m
dF1
y
P2
líquido
A
z
z
dF2
24
M
1,5 m
D


A
ydF1 
0
0
1,5 m
D

yP1dA1 
0

zP2dA 2  0
0
1,5 m
D
dA
 yρgh

1
0
D

0

zdF2  0
1

P1
dA
 zρgh

2
2
P2
0
yρ g D  y W
d
y



dA1
1,5 m

0
D
1,5 m
0
0
zρ g D W
 dz

dA 2
 yD  y dy   zDdz
25
1, 5 m
y 
  z 
 Dy
 2  3   D 2 

0
0
2
3
D
2
1,5m
DD
D

 D
2
3
2
D3
D3

 Dx1,125m2
2
3
D3
 Dx1,125m2
6
2
3
2
D  2,6m
26
Exemplo 04: A comporta de 2 m de comprimento é articulada em H. Sua
largura de 2 m é normal ao plano da Figura. Calcule a força Ft requerida em
A para manter a comporta fechada.
Dado: água = 9810 N/m3

Patm ( 0)
z
L = 2m
1m
h
H
h1
Ft
30
dF
30 A
água
y
27
M
H
 Ft L 
 ydF  0
L
1
1
1
Ft 
ydF 
yPdA 
yPL dy
L
L
L 0



L

Ft  yPdy
0
P  P atm  ρ água gh  γ água h
h  1m  h1  1m  ysen30 0
P  γ água  1m  ysen30
0
dA  Wdy
W  L  2m

28
L
Ft  yγ água 1m  ysen300 dy 

0
L

γ água 1m.y  y 2sen300 dy
0
L  2m
y
y

0
Ft  γ água 1m.
 sen30 
2
3

0
2
(2m) 3 1 
 (2m)
Ft  γ água 1m.


2
3
2


N  4m 2
8m3 
Ft  9810 3 1m

m 
2
6 
Ft  32700 N
2
3
Ft  32,7 kN
29
Exemplo 05: O nível de água é controlado por uma comporta plana de
espessura uniforme e articulado em A. A largura da comporta, normal ao
plano da Figura, é W = 10 ft. Determine a massa M, necessária para manter
o nível à profundidade H, ou menos, se a massa da comporta for desprezível.
Dado: água = 1,94 slug/ft3

y
z
h
H = 4 ft
dF

D
A
W 
M
30
M
A
 Wz 2,5ft 

ydF  0
Wcosθ 2,5ft   ydF   yPdA 
7,5ft
 yPwdy
0
7,5ft
Mgcosθ 2,5ft   yPwdy
0
P  P atm  ρ água gh  γ água h
h  4ft  D  4ft  ysenθ
4ft
senθ 
 0,53  θ  arcseno(4/7,5)  θ  32,230
7,5ft
P  γ água h  γ água 4ft  ysenθ 
31
7,5ft
Mgcosθ 2,5ft   yγ água 4ft  ysenθ wdy
0
wg ρ água
M 
2,5ft g cosθ 
7,5ft

y
4
ft

 y 2senθ dy
0
7,5ft
wρ água  y 2
y3

M 
4ft  senθ 

2,5ft cosθ   2
3
0
M 
10ft 1,94slug/ft 3   (7,5ft)2
2,5ft cos32,230  
2
(7,5ft)3
0
4ft 
sen32,23 
3

M  344 slug
32
Exemplo 06: A comporta AOC mostrada na Figura tem 6 ft de largura e é
articulada ao longo de O. Desconsiderando o peso da comporta, determine a
força na barra AB.
Dado: água = 1,94 slug/ft3 ; 1slug = lbf.s2/ft ; g = 32,2 ft/s2
Ft
33
y
Ft
A

3 ft
B
h1
12 ft
h2
dF1
y
C
O
8 ft
z
dF2
z
6 ft
34
M
Ft 15ft
Ft 15ft
O


  ydF   zdF
  yP dA   zP dA
 Ft 15ft 
zdF2 
1
1
2
1
12 ft
Ft 15ft 
ydF1  0
2
2
6ft
 yP Wdy   zP Wdz
1
0
2
0
P1  P atm  ρ água gh1  γ água h1
h1  12ft  y
P1  γ água 12ft  y 
P2  P atm  ρ água gh 2  γ água h 2
h 2  12ft
P2  γ água 12ft
35
12 ft
Ft 15ft 
6ft
 yP Wdy   zP Wdz
1
2
0
0
12 ft
Ft 15ft 
 yγ
0
6ft
água
12ft  y Wdy   z12ft Wdz
0


2
Ft 15ft  Wγ água  y12ft  y dy  12ft zdz 
 0

0
2
3 12ft
2 6ft
 y
y 
z  

Ft 15ft  Wγ água   12ft    12ft  
3 0
2 0 

2
12 ft

6ft

36
3 12ft
2  6ft 
  y 2

y
z

Ft 15ft  Wρ água g   12ft 

12ft


 
2
3
2
0

 0 
 




lbf.s 2 
ft   12ft 2
12ft 3 
6ft 2 
Ft 15ft  6ft 1,94 4  32,2 2  
12ft 
  12ft

2
3
2
ft
s









lbf
Ft 15ft  374,51 4 ft 864ft 3  576ft 3  216ft 3
ft

 




Ft  1797,6 lbf
37