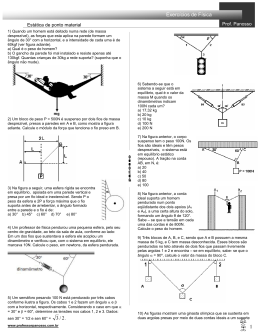
Física Fácil – Prof. Erval Oliveira
1. PONTO MATERIAL E CORPO EXTENSO
Um corpo é considerado um ponto material
quando seu tamanho é desprezível em
comparação com as distâncias envolvidas no
fenômeno em estudo.
Isto significa que o tamanho do corpo não tem a
menor importância no fenômeno estudado.
Entenda, contudo, que ponto material tem
MASSA e essa em geral não é desprezível.
Em contraposição, quando o corpo não é um
ponto material, isto é, seu tamanho é importante
no estudo do fenômeno, falamos em CORPO
EXTENSO.
2. EQUILÍBRIO DE UM PONTO MATERIAL
Um ponto material está em equilíbrio, em
relação a um determinado referencial, quando a
resultante das forças agentes no ponto for
constantemente nula.
Nestas
condições,
sendo
b) Quando um ponto material está sujeito à ação
de três forças, para o equilíbrio devemos ter,
sempre, a resultante de duas delas igual em
módulo e direção e sentido contrário com
relação à terceira força.
Observe-se que, neste caso, a linha poligonal
das forças será um triângulo, isto significa que,
necessariamente, as três forças devem ser
coplanares.
 

F1 , F2 ,..., Fn um
sistema de forças coplanares que agem sobre
um ponto material em equilíbrio, devemos ter:
  

F  F1  F2  ...  Fn  O O estudo do equilíbrio
pode ser feito através dos métodos:
a) método da linha poligonal das forças:
A linha poligonal das forças deve ser fechada.
EXERCÍCIO
1º) Um ponto material está sendo solicitado por
duas forças de mesma intensidade, tal que a
intensidade de uma delas é igual à intensidade
da resultante. Qual o ângulo formado pelas duas
forças?
2º) Considerando na figura  =45 , a aceleração
2
da gravidade igual a 10 m/s e a massa do corpo
suspenso igual a 6kg, determine as tensões nos
fios AB e BC.
0
b) método das projeç6es:
As somas algébricas, das projeções das forças
sobre dois eixos perpendiculares entre si, e
pertencentes ao plano das forças são nulas.
3º) Uma corda de peso desprezível sustenta um
corpo de peso P, conforme a figura.
Determine as intensidades das forças de tração
nos fios AB e BC.
3. CASOS PARTICULARES
a) Quando um ponto material está sujeito à ação
de duas forças, para o equilíbrio as forças
devem ter o mesmo módulo e direção, mas com
sentidos opostos.
4º) A corda presa em A passa pela polia B e
sustenta dois pesos P e Q.
9º) No exercício anterior, qual o peso P2
necessário para manter o equilíbrio?
Sendo Q = 1ON, pode-se afirmar que a tração
na corda AC é igual a:
a) 5N b) 10N c) 15N d) 20N e) 15N
10º) O esquema anexo representa um sistema
em equilíbrio. O fio é leve e flexível.
5º) Retome o exercício anterior. O peso P é
igual a:
a) 6N
b) 12N
c) 3N
d) 9N
e) 15N
6º) Uma esfera é presa pelo seu centro a fios
inextensíveis, de massas desprezíveis, que
passam por duas roldanas, também de massas
desprezíveis e livres de atrito.
Na extremidade dos fios, estão dois corpos de
pesos P1 = 20N P2 = 10N, conforme mostra a
figura.
Estática dos corpos extensos:
1. MOMENTO DE UMA FORÇA
Consideremos uma forçar aplicada em P e um
ponto O. Seja d a distância do ponto O até a
linha de ação da força.
Define-se MOMENTO ESCALAR M da força F
em relação ao ponto O pela relação:
7º) A esfera representada na figura tem peso
150N e encontra-se em equilíbrio
pendurada em uma parede por
uma corda de comprimento  =. 2R
(sendo R o raio da esfera).
A tração exercida pela esfera sobre
a corda vale:
a) 150N b) 75N c) 300N
d) 212N e) 173N
8º) O esquema representa um sistema em
equilíbrio. Sabe-se que o peso P do corpo
apoiado sobre o plano inclinado é 200 kgf e P1 =
20 kgf.
Desprezando as forças de atrito na polia e no
plano, determine a reação R do plano sobre o
corpo.
O momento poderá ser positivo ou negativo,
dependendo de uma convenção de sinais
preestabelecida.
Vamos adotar como positivo o sentido antihorário.
Deste modo temos:
M1= - F1 .d1 e M2= + F2 . d2
Nota: A distância d é denominada BRAÇO da
força F e o ponto O é denominado PÓLO.
2. EQUILÍBRIO DOS CORPOS EXTENSOS
Um corpo extenso está em equilíbrio, em
relação a um determinado referencial, quando:
a) a resultante das forças que atuam sobre o


corpo é nula (F  0)
b) a soma algébrica dos momentos das forças
que atuam no corpo, em relação a um ponto
qualquer, é nula.
5º) Para que uma barra AB de peso 1000 kgf
fique em equilíbrio como indicado na figura, foi
necessário distender, de 20 cm, a mola cuja
constante é igual a 100 kgf/cm.
Determine o peso da carga pendurada.
( M  0)
Para um corpo extenso em equilíbrio, sob ação


de forças coplanares, a condição (F  0) se
traduz em duas equações escalares: F x = 0 e
Fy = 0.
EXERCÍCIO
1º) O esquema representa uma alavanca leve,
suspensa pelo centro e suportando quatro
cargas (em gramas-força). Cada divisão na
alavanca mede 10 cm. Observar a posição das
cargas suspensas.
Determinar o valor do peso P indicado,
sabendo-se que a alavanca permanece em
equilíbrio.
2º) A figura mostra uma régua homogênea em
equilíbrio estático, sob ação de várias forças.
Quanto vale
F, em N?
a) 1
b) 2
e) 2,5
d) 3
e) 5
3º) O esquema mostra uma barra rígida e
homogênea de peso 80 N e comprimento L =
1,20 m, suspensa por um fio. Um bloco de peso
20 N está pendurado na extremidade da barra.
Se o sistema se encontra em equilíbrio, qual é o
valor de x?
a) 0,60 m
b) 0,48 m
e) 0,40 m
d) 0,30 m
e) n.d.a.
4º) João e Paulo suportam nos ombros uma
haste leve de 3,0 m na qual dependuram uma
pedra de 60 kg, portanto com peso próximo de
600 N. O ponto de suspensão dista 1,0 m de
João. Qual a carga que João suporta?
6º) A figura representa uma escada apoiada
contra uma parede com duas
das forças que atuam sobre ela:
o peso P e a força F exercida
pela parede.
As componentes horizontal e
vertical que o chão exerce
sobre a escada são melhores
representadas por:
7º)Um bloco de massa igual a 240kg está
suspenso conforme é apresentado na figura
abaixo. Considerando desprezível a massa da
barra AB, qual a tração no cabo BC. É dado g =
2
10 m/s .
8º) AB é uma barra rígida, sem peso, encostada
entre duas paredes indeformáveis OA e OB,
formando entre si um ângulo de 90° . AB forma
com OB o ângulo de 450 (OA 10 m e OB =
lOm). No ponto mádio de AB coloca-se a massa
de 10 kg (g 10 m/s2). Na figura estão
representadas as forças que comparecem. Com
a barra em equilíbrio, quais são os valores de
F1, F2 e F3?
a) 50, 100, 50
b) 50, 50, 100
c) 100, 50, zero
d) 100, 100,50
e) 50,50, 50