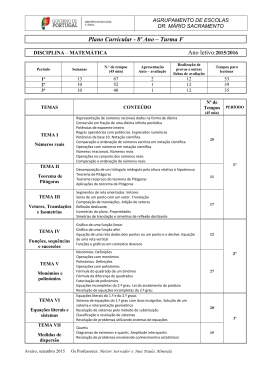
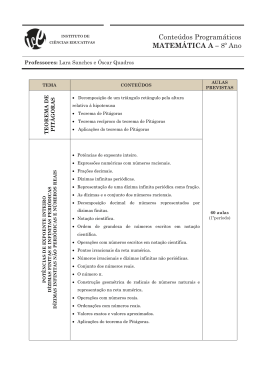
Matlab 2
Processamento Simbólico
Polinómios e Equações
Gráficos
Matlab
1.
Exercício 2
Iniciar o programa Matlab.
Há duas formas:

Fazer duplo-clique sobre o atalho

Menu Iniciar > Programas > Matlab > Matlab 5.3
, existente no ambiente de trabalho do Windows
Processamento Simbólico
Neste exercício abordamos o processamento de expressões simbólicas, tais como:
3x 2  5x  1 v 
cos( x 2 )
d
2x 2
dx
f 
x2
1 x
dx
O Matlab usa objectos simbólicos para representar variáveis e expressões. Uma expressão simbólica é uma
expressão que contém objectos simbólicos e internamente, um objecto simbólico é uma estrutura de dados do
tipo cadeia de caracteres (string).
Criação e Utilização de Objectos Simbólicos
Os objectos simbólicos podem ser criados através das funções sym e syms, cujos formatos são os seguintes:

v = sym ( ‘ expressão ’ )

syms v1 v2 ... vn
( cria a variável simbólica v para representar a expressão )
( cria as variáveis simbólicas v1, v2, ..., vn )
1. Criar a variável simbólica e para representar a expressão
2 k  5 1:
» e = sym ( ‘ 2 * k + sqrt(5) = 1’ )
2. Criar as variáveis simbólicas x, y e z:
» syms x y z
Nota: Reparar que as variáveis simbólicas não precisam de guardar um valor predefinido como no
processamento numérico.
3. Criar a variável f para representar a expressão
x y
:
x2
» f = (x+y) / (x-2)
Nota: Este comando cria uma variável simbólica (f) porque a expressão contém pelo menos uma variável
simbólica (definida previamente).
4. Criar as seguintes variáveis v e M:
a)
v
1
2w
( para representar a expressão
1
2w
)
» syms w
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 1/12
Matlab
Exercício 2
» v = 1 / sqrt ( 2 * w )
Nota: Depois de criar uma variável simbólica, esta pode ser usada em expressões, da mesma maneira
que as variáveis numéricas.
b)
a b 
M 

c d 
( para representar uma matriz 2X2 )
» syms a b c d
» M =  a, b ; c, d 
5. Calcular o determinante da matriz M.
» det ( M )
( Solução (S) = a * d – b * c )
Substituição de Variáveis
Numa expressão simbólica, para substituir uma variável por um valor numérico usa-se a função subs. O seu
formato é o seguinte:

( retorna a expressão f com a variável x substituída pelo valor a )
subs (f, x, a)
Esta função é particularmente importante para determinar o valor duma função.
1. Definir a função
f ( x)  2 x 2  3x  5 :
»f=2*x^2+3*x-5
2. Calcular o valor de f (2):
» subs(f, x, 2)
(S=9)
Operações Básicas ( Soma, Subtracção, Multiplicação, Divisão e Potenciação )
Usam-se os operadores habituais e que foram apresentados no exercício anterior Matlab_1 sobre o processamento
numérico ( +, -, *, /, ^).
1. Definir a função
g ( x)  x 2  x  7 :
»g=x^2–x+7
2. Calcular as seguintes operações:
a)
f g
(»f+g)
(S=3*x^2+2*x+2)
b)
f g
(»f*g)
(S=(2*x^2+3*x–5)*(x^2–x+7))
c)
f
3x
( » f ^ (3 * x) )
( S= ( 2 * x ^ 2 + 3 * x – 5 ) ^ ( 3 * x ) )
Somatórios
Os somatórios são calculados através da função symsum e a sua forma geral é a seguinte:
b

symsum(f, x, a, b)
( retorna

f (x)
)
a
1. Calcular:
n
a)

( 2n  1) 2
( » symsum ( (2*n-1)^2, n, 1, n ) )
(S=11/3*n+8/3-4*(n+1)^2+4/3*(n+1)^3)
1
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 2/12
Matlab
Exercício 2
10
b)

(2n  1) 2
( » symsum ( (2*n-1)^2, n, 1, 10 ) )
( S = 1330 )
1

c)

1
1
( 2n  1) 2
( » symsum ( 1/(2*n-1)^2, n, 1, inf ) )
( S = 1/8*pi^2 )
Limites
Para o cálculo de limites de expressões simbólicas usa-se a função limit e podemos usar as seguintes formas:

limit (f, x, a )
( retorna o limite de f quando x  a )

limit (f, x, a, ‘right’ )
( retorna o limite de f quando x  a+ )

limit (f, x, a, ‘left’ )
( retorna o limite de f quando x  a- )
f (x ) 
1. Definir a função
sen( x)
x
:
» f = sin(x)/x
lim
2. Calcular o x
0
f ( x) :
» limit ( f, x, 0 )
(S=1)
3. Calcular os seguintes limites:
a)
b)
c)
1
lim (1  ) x
x
( » limit ( (1+1/x)^x, x, inf ) )
( S = exp(1) )
lim
1
x
( » limit ( 1/x, x, 0, ‘right’ ) )
( S = inf )
lim
1
x
( » limit ( 1/x, x, 0, ‘left’ ) )
( S = -inf )
x 
x 0
x  0
Derivadas
Para a derivação de expressões simbólicas usa-se a função diff e a sua forma geral é a seguinte:

diff (f, x, n)
1. Definir a função
( retorna a n-ésima derivada da função f em ordem a x )
f ( x)  ax 3  x 2  bx  c :
»f=a*x^3+x^2–b*x-c
2. Calcular as suas derivadas de 1ª e 2ª ordem em relação à variável x :
a)
d
f (x)
dx
( » diff ( f, x, 1 ) )
(S=3*a*x^2+2*x-b)
b)
d2
f (x )
dx 2
( » diff ( f, x, 2 ) )
(S=6*a*x+2)
3. A função diff também opera sobre matrizes.
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 3/12
Matlab
Exercício 2
a) Criar a matriz simbólica
 ax
M  3
cx
bx 2 

dy 
b) Calcular as derivadas de 1ª ordem dos elementos da matriz M em relação a x:
» diff ( M, x, 1 )
(S=
)
Integrais
Para a integração de expressões simbólicas usa-se a função int e podemos usar as seguintes formas:

int (f, x)
( retorna o integral indefinido de f em relação à variável x )

int (f, x, a, b)
( retorna o integral definido de f em relação à variável x no intervalo
entre a e b )
1. Definir a função
g ( x)  seno(2 x  y ) :
» g = sin ( 2 * x + y )
2. Calcular os seguintes integrais :
a)
 g ( x) dx
( » int ( g, x ) )
( S = -1 / 2 * cos ( 2 * x + y ) )

b)
 g ( y ) dy
( » int ( g, y, 0, pi ) )
( S = 2 * cos(x) ^ 2 – 1 + cos( 2 * x ) )
0
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 4/12
Matlab
Exercício 2
Simplificação e Formatação de Expressões
O Matlab oferece diversas funções para simplificar ou modificar o formato de expressões simbólicas.
Para simplificar podemos usar a função simple.
1. Simplificar o último resultado obtido (ans), usando o seguinte comando:
» r = simple( ans )
( S = 2 * cos ( 2 * x ) )
Esta função usa vários métodos de simplificação e fornece o resultado mais curto. Para evitar a
apresentação de todos esses métodos, atribui-se a função simple a uma variável (como neste caso).
Para formatar uma expressão simbólica podemos usar as seguintes funções:

expand( p )
( expande todos os termos de p )

factor( p )
( tenta apresentar p como um produto de polinómios )

collect( p , v )
( escreve p em termos de potências de v )
2. Definir a função
p ( x )  ( x 2  1)( x  2)( x  3) :
»p=(x^2–1)*(x–2)*(x–3)
3. Determinar uma expressão equivalente de p, desenvolvendo os produtos :
» expand( p )
(S=x^4–5*x^3+5*x^2+5*x-6)
4. Determinar uma expressão equivalente de p, decompondo a expressão num produto de polinómios:
» factor( ans )
5. Definir a expressão
(S=(x–1)*(x–2)*(x–3)*(x+1))
g ( x)  4 x 2  2 x  x 2  1  3x  5 :
»g=4*x^2–2*x+x^2–1–3*x+5
Nota: Reparar que o Matlab guarda a expressão simplificada ( g ( x )
 5 x 2  5 x  4 ),
agrupando os
termos de x do mesmo grau.
6. Definir a expressão
p( x)  2 x  xy  5 y  y 2  2
»p=2*x+x*y+5*y+y^2+2
7. Determinar a expressão equivalente de p, agrupando os termos de x do mesmo grau:
» collect ( p )
(S=(y+2)*x+2+5*y+y^2)
8. Determinar a expressão equivalente de p, agrupando os termos de y do mesmo grau:
» collect ( p , y )
(S=y^2+(x+5)*y+2*x+2)
Precisão dos Resultados
O processamento simbólico é muito mais preciso que o processamento numérico, porque as operações
com valores numéricos introduzem erros de arredondamento e que se vão acumulando em operações
sucessivas, enquanto que as operações simbólicas como não efectuam cálculos numéricos, não geram
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 5/12
Matlab
Exercício 2
esses erros. Os erros de arredondamento surgem porque a precisão numérica é limitada pelo número
de dígitos utilizados por cada operação.
Para usarmos o processamento simbólico no cálculo de expressões numéricas, estas precisam de ser
previamente definidas como constantes simbólicas, como veremos na secção seguinte.
Funções de Conversão
O Matlab fornece funções que permitem converter valores numéricos em constantes simbólicas e vice-versa. As
constantes simbólicas são expressões simbólicas sem variáveis.

sym( ‘ n ’ )
( retorna a representação simbólica do valor numérico n )

double( c )
( retorna o valor numérico da constante simbólica c com precisão dupla )
1. Converter o seguinte valor numérico
(1  5 ) / 2
numa constante simbólica :
» c = sym ( ‘ (1 + sqrt(5))/2 ’ )
Nota: Reparar que a variável simbólica c guarda a expressão e não o seu resultado, como acontece no
processamento numérico.
2. Converter a constante simbólica c no seu valor numérico:
» double(c)
( S = 1.6180 )
Polinómios e Equações
A determinação das raízes dum polinómio e a resolução de sistemas de equações lineares podem ser resolvidos
através do processamento simbólico, usando a função solve.
Raízes dum Polinómio
A função solve pode ser usada no seguinte formato:

solve ( p ) ( devolve as raízes do polinómio p (variável simbólica) em relação à variável independente
mais próxima alfabeticamente de x )
1. Definir o polinómio
p1  x 2  2 x  3 :
» p1 = x ^ 2 + 2 * x - 3
2. Determinar as raízes do polinómio p1:
» solve( p1 )
3. Definir o polinómio
( S = ( -3 , 1 ) )
p 2  x 2  ax  b :
» p2 = x ^ 2 + a * x - b
4. Determinar as raízes do polinómio p:
» solve( p2 )
Processamento Simbólico, Polinómios, Equações e Gráficos
(S=(
))
Pág. 6/12
Matlab
Exercício 2
Resolução de uma Equação Linear
Podemos usar a função solve no formato apresentado anteriormente, em que o p passa a representar a equação
a resolver.
1. Criar a variável simbólica e para representar a equação
2x  3  5 :
» e = sym ( ‘ 2*x + sqrt(3) = 5 ’ )
Nota: É usada esta função sym por causa do sinal = da equação.
2. Resolver a equação :
» solve( e )
( S = -1 / 2 * 3 ^ ( 1 / 2 ) + 5 / 2 )
Resolução de um Sistema de Equação Lineares Possível e Determinado
A função solve também pode ser usada no seguinte formato:

S = solve ( ‘e1’, ‘e2’ , ..., ‘en’) ( determina a solução do sistema de n equações (e1, e2, ..., en) em
função das variáveis-padrão independentes (x, y, ...) e guarda-a na variável S do tipo registo ou
estrutura )
1. Criar as variáveis simbólicas (e1, e2) para representarem as equações do seguinte sistema
x  y  2

 x  y 1
» e1 = sym ( ‘ x + y = 2 ’ )
» e2 = sym ( ‘ x - y = 1 ’ )
2. Resolver o sistema de equações:
» S = solve( e1, e2 )
(S é uma estrutura que guarda as variáveis x e y )
3. Determinar as soluções de x e y:
» S.x
(S=3/2)
» S.y
(S=1/2)
4. Criar as variáveis simbólicas (e3, e4) para representarem as equações do seguinte sistema de equações
lineares:
ax  by  2
cx  dy  1
5. Resolver o sistema de equações:
» S = solve( e3, e4 )
6. Determinar as soluções de x e y:
» S.x
(S=(b+2*d)/(a*d+b*c))
» S.y
(S= - ( a – 2 * c ) / ( a * d + b * c ) )
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 7/12
Matlab
Exercício 2
Resolução de um Sistema de Equação Lineares Indeterminado
7. Resolver o seguinte sistema de equações indeterminado (nº de equações é inferior ao nº de incógnitas):
 ax  by  z  1

x  2 y  3z  c
( S.x = -( 2 * z – 2 – 3 * z * b + c * b ) / ( 2 * a – b ) )
( S.y = ( -3 * a * z + a * c + z – 1 ) / ( 2 * a – b ) )
Resolução de um Sistema de Equação Lineares Sobredeterminado
8. Resolver o seguinte sistema de equações sobredeterminado (nº de equações é superior ao nº de incógnitas):
 x y1
x  2 y  3

 5 x  5 y   5

( S.x = - 1 )
( S.y = 2 )
Gráficos
Apenas são abordados os gráficos de linhas bidimensionais.
O Matlab cria os gráficos numa janela chamada Janela de Figuras.
Gráficos de Linhas Bidimensionais
Os gráficos de linhas bidimensionais podem ser criados a partir duma expressão simbólica ou de vectores de
dados.
Dados definidos por expressões simbólicas:
Usamos a função ezplot no seguinte formato:

ezplot ( f, a, b )
( cria gráfico de f=f(x) no intervalo a < x < b )
1. Criar um gráfico de linhas bidimensional da função seno no intervalo -2 < x < 2:
» ezplot( ‘ sin(x) ’ ,  -2*pi, 2*pi  )
( cria gráfico numa janela de figuras )
2. Formatar o gráfico de acordo com a figura seguinte, recorrendo às ferramentas disponíveis no menu Tools.
3. Guardar o gráfico na sua pasta pessoal:

Menu File > Save
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 8/12
Matlab
Exercício 2
Podemos adicionar novas curvas ao gráfico existente, usando o comando hold. Depois de executado o comando
hold on, o Matlab adiciona as novas curvas ao gráfico existente. Se os novos dados não se ajustarem aos limites
actuais dos eixos, estes são reescalados. Para voltar a criar um novo gráfico é preciso usar o comando hold off.
4. Instruir o Matlab a adicionar uma nova curva ao gráfico existente.
» hold on
5. Criar a curva da função coseno no intervalo -2 < x < 2:
» ezplot( ‘ cos(x) ’ ,  -2*pi, 2*pi  )
6. Formatar o gráfico de acordo com a figura seguinte:
7. Guardar o gráfico na sua pasta pessoal.
8. Instruir o Matlab a criar novos gráficos.
» hold off
9. Criar a curva da função seno no intervalo 0 < x < 2:
» ezplot( ‘ sin(x) ’ ,  0, 2*pi  )
10. Guardar o gráfico na sua pasta pessoal.
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 9/12
Matlab
Exercício 2
Dados definidos por vectores:
Usamos a função plot nos seguintes formatos:

plot ( x, y )

plot ( x1, y1, x2, y2, ..., xn, yn ) ( cria gráfico com múltiplas curvas: y1(x1), y2(x2), ..., yn(xn) )
( cria gráfico y(x) no intervalo xmin < x < xmax )
Notas:  Os pares de vectores de dados (x, y) têm de ter a mesma dimensão;
 As curvas são criadas unindo os pontos por linhas rectas.
Comecemos por criar o gráfico do seno(x) no intervalo -2 < x < 2.
1. Criar os vectores de dados x e y, com 30 elementos:
» x = linspace ( 0, 2*pi, 30 )
» y = sin ( x )
2. Criar o gráfico y(x):
» plot ( x, y )
3. Guardar o gráfico na sua pasta pessoal.
Vamos agora criar um gráfico com duas curvas, seno(x) e cos(x), no intervalo -2 < x < 2:
1. Criar o vector x2, com 10 elementos:
» x2 = linspace ( -2*pi, 2*pi, 10 )
2. Criar o vector y2, com 10 elementos:
» y2 = cos ( x2 )
3. Criar o gráfico:
» plot ( x, y, x2, y2 )
4. Formatar o gráfico de acordo com a figura seguinte:
5. Guardar o gráfico na sua pasta pessoal.
EXTRA:
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 10/12
Matlab
Exercício 2
1.
Criar a variável simbólica E para representar a equação:
2.
Determinar a solução da equação da alínea anterior.
3.
Definir a variável F para representar a função
4.
Determinar o valor de f (5)
5.
Definir a variável G para representar a função
6.
Calcular:
n
a)

2 ln( x )  5 3  2
( S = exp(1/2*3^(1/5)+1) )
f ( y )  ln( y )  e y
( S = 13.7919 )
g ( z )  4 z 2  cos( z )
(2 n  5)
(S=2^(n+1)+5*n-2)
1
b)
1
lim ( )
x  x
c) lim (
x 0
(S=0)
cos( x)
)
x
( S = inf )
d)
d2
g ( z)
dz 2
( S = 8 - cos( z ) )
e)
 g ( z) dz
( S = 4 / 3 * z ^ 3 + sin( z ) )

f)
 tg ( x) dx
(S=0)

cos 2 ( x)  sen 2 ( x)
7.
Simplificar a expressão:
8.
Desenvolver os produtos da expressão:
9.
Decompor a expressão num produto de polinómios:
(S=1)
( x  1)( x  1)
(S=x^2-1)
( x 2  1)
(S=(x–1)*(x+1))
10. Simplificar a expressão agrupando os termos de y do mesmo grau:
2 xy  4 y 2  yx 2  5
(S=4*y^2+(2*x+x^2)*y+5)
11. Definir a constante simbólica C como representante da expressão numérica:
ln(4)  2
12. Determinar o valor numérico da constante simbólica C da alínea anterior.
( S = -0.6137 )
13. Determinar as raízes do polinómio: p( x)  x 2  ax  x  a
( S = ( 1, -a ) )
14. Resolver o seguinte sistema de equações:
3x  ay  1

 x y 5
15. Criar um gráfico de linhas bidimensional para representar as funções
intervalo
( S.x = ( -1 + 5 * a ) / ( -3 + a ) )
( S.y = 14 / ( -3 + a ) )
f (x ) 
x
3
4
e
g ( x)  x  1
no
x  0,10 . O gráfico deve apresentar a seguinte formatação:
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 11/12
Matlab
Exercício 2
Processamento Simbólico, Polinómios, Equações e Gráficos
Pág. 12/12