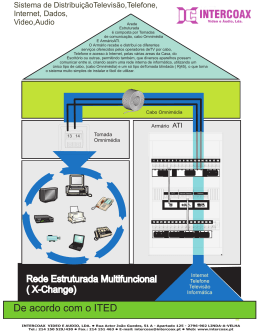
Exercı́cio 1. Calcule o campo magnético, em todo o espaço, gerado por um
cabo coaxial percorrido por correntes de mesma intensidade mas de sentidos
opostos em cada face.
Figura 1: Cabo coaxial
1
Resolução. Vamos dividir o espaço em 4 regiões e aplicar a Lei de Ampère
para cada uma delas:
• Para r < a:
Para determinar a corrente interna à amperiana, vamos considerar que
a densidade de corrente ao longo do cabo é constante e igual à j, logo
sendo πr2 a área delimintada pela amperiana:
j=
I
Iint
= 2
2
πr
πa
Iint =
r2
a2
(1)
(2)
Aplicando a Lei de Ampère:
B2πr = µ0 I
r2
~ = µ0 Ir θ̂
→B
2
a
2πa2
• Para a < r < b:
A corrente interna à amperiana será sempre a corrente total que passa
pelo cabo interno, logo pela Lei de Ampère:
~ = µ0 I θ̂
B2πr = µ0 I → B
2πr
• Para b < r < c:
A corrente interna à amperiana será a corrente total que passa pelo
cabo interno menos a corrente que passa pela porção do cabo externo
delimitada pela curva. Considerando também a densidade de corrente
constante no cabo externo:
Iint = I −
2
r 2 − b2
c 2 − b2
(3)
Aplicando a Lei de Ampère:
µ0 Iπ (r2 − b2 )
~ = µ0 I
B2πr = µ0 I −
θ̂ → B
2
2
π (c − b ) 2πr
2
2
c
−
r
~ = µ0 I
B
θ̂
c 2 − b2
r 2 − b2
1− 2
θ̂
c − b2
• Para r > c:
A corrente interna à amperiana será a soma das correntes que passam
pelo cabo interno e pelo cabo externo. Como as duas correntes possuem
a mesma intensidade mas possuem sentidos opostos, a soma sempre será
nula. Então, pela Lei de Ampère:
~ =0
B
3
(4)