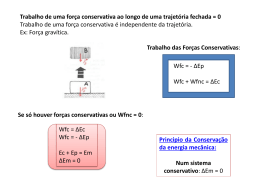
Unidade 11 – Dissipação e
Conservação da Energia Mecânica
Sistemas Dissipativos
Sistemas Conservativos
Introdução
Conforme a interpretação que fizemos do Teorema da Energia
Mecânica, dependendo do valor do trabalho realizado pelas forças
conservativas que agem sobre um corpo, podemos ter decréscimo,
manutenção ou acréscimo no valor da energia mecânica que ele
possuía inicialmente.
No caso, por exemplo, de um foguete, devido à força não conservativa
que o propulsiona para cima durante o lançamento, ocorre um
aumento de energia mecânica.
Inicialmente, por estar em repouso no solo, um foguete não possui
energia cinética nem energia potencial gravitacional em relação ao
chão.
Ao realizar trabalho motor, a força propulsora fornece energia e o
foguete ganha energia cinética (aumenta sua velocidade) e energia
potencial gravitacional (aumenta sua altura em relação ao solo).
Apesar de casos como esses serem muito comuns em nosso dia a
dia, enfatizaremos as situações nas quais a quantidade de energia
mecânica de um sistema de corpos diminui ou se mantêm constante.
Sistemas Dissipativos
Quando tratamos de Física, o verbo dissipar
significa transformar qualquer modalidade de
energia em energia, normalmente, térmica.
Assim, quando um ferro elétrico é ligado, ocorre
dissipação de energia, pois energia elétrica é
convertida em energia térmica.
De maneira similar, quando o motor de um carro
funciona, ele esquenta bastante e dissipa energia,
pois transforma parte da energia química contida
nas moléculas do combustível usado em energia
térmica.
Sistemas Dissipativos
Quando o trabalho das forças não conservativas que agem
num corpo (τFñcons) é resistente, ou seja, negativo, ocorre
diminuição em sua energia mecânica.
Isso é fácil de perceber, se recordarmos o Teorema de Energia
Mecânica (τFñcons = EMf - EMi) : como EMf – EMi < 0 , então EMf <
EMi.
Essa dissipação de energia mecânica acontece devido ao fato
de termos forças não conservativas contrárias ao movimento
realizado pelo corpo.
A título de estabelecermos uma classificação, quando isso
ocorre, dizemos que temos um sistema dissipativo.
Dissipação de energia mecânica
O que ocorre com um objeto, quando lançado sobre uma
superfície áspera? Como funcionam os paraquedas?
Essas perguntas estão diretamente relacionadas à dissipação
de energia mecânica pela realização de trabalho de forças não
conservativas.
No caso de um corpo que escorrega sobre uma superfície não
lisa, a força de atrito devido ao contato com o solo realiza
trabalho resistente. Se, por exemplo, isso acontecer num plano
horizontal, ocorrerá somente diminuição de energia cinética
(redução de velocidade). Como resultado, teremos dissipação
na energia mecânica do corpo.
Dissipação de energia mecânica
Quando uma pessoa salta de um avião e aciona o
paraquedas, após uma brusca redução de rapidez, a
velocidade de queda passa a ser constante até o
momento da chegada ao solo.
Durante esse período final da descida, ocorre
diminuição de energia mecânica devido ao fato de a
resistência do ar realizar trabalho resistente.
Agora, como a velocidade da pessoa é constante e
a altura dela em relação ao solo diminui, há
dissipação de energia mecânica com a perda de
energia potencial gravitacional.
Você sabia?
A mais radical montanha-russa
do mundo não é russa, mas é
americana. É a Top Thrill
Dragster, localizada no parque
Cedar Point, na cidade de
Sandusky, em Ohio.
Nesse brinquedo, os passageiros
chegam a atingir a altura de 128
metros e a velocidade de 193
Km/h ao chegarem ao ponto
mais baixo do percurso.
Observe os cálculos a seguir,
supondo que os carrinhos (que,
juntos, totalizam massa igual a
m) estejam a uma altura
praticamente nula em relação ao
solo, ao passarem no ponto mais
baixo da trajetória descrita:
a)Energia potencial gravitacional
no ponto mais alto(h = 128 m)
Ep = m . g . h
Ep = m . 10 . 128 = 1280 m
b)
Energial cinética no ponto mais baixo
(V = 193 km/h = 53,6 m/s )
m.v 2 m.53,6 2
Ec =
=
= 1436 m
2
2
Você sabia?
Pelos cálculos anteriores, podemos perceber que, no final da
descida, os carrinhos têm mais energia cinética do que
possuíam de energia potencial no ponto mais alto da
montanha-russa.
Isso causa uma impressão de que energia está surgindo
espontaneamente. Mas, como sabemos, energia não pode ser
criada nem destruída. Então, como podemos explicar tudo
isso?
É difícil sabermos exatamente o que acontece com os
carrinhos desse brinquedo radical sem o conhecermos em
detalhes, mas podemos afirmar que duas hipóteses são
válidas:
Você sabia?
a) No ponto mais alto da trajetória, os carrinhos não estavam
em repouso e, portanto, não possuíam apenas energia
potencial.
Dessa forma, se conhecêssemos a velocidade deles nessa
posição, poderíamos calcular a energia cinética que possuíam.
Obviamente, perceberíamos que a energia mecânica dos
carrinhos seria maior que apenas a energia potencial
(resultado obtido no primeiro cálculo).
b) Durante partes do percurso, com o objetivo de repor as
dissipações de energia mecânica causadas pelo atrito com o
trilho e pela resistência do ar, motores elétricos impulsionam o
carrinho e o fazem adquirir energia cinética e/ou potencial.
Dissipação de energia mecânica
Bem, mas surge, nesse momento, uma nova
pergunta: se energia não pode ser criada,
nem destruída, como podemos ter
diminuição de energia mecânica nos
sistemas classificados como dissipativos?
Começaremos a buscar a resposta para isso
a partir de agora.
Lei da Conservação da Energia
Já conhecemos a famosa Lei de Lavoisier: “Na natureza nada se
cria, nada se perde, tudo se transforma”.
Apesar de ela ter sido originalmente enunciada pensando-se na
massa de corpos, curiosamente, vale também para outras grandezas
físicas, como energia.
Assim como ocorre com qualquer lei científica, a de Lavoisier será
considerada verdadeira, enquanto não for encontrado nenhum
exemplo ou evidência de sua falibilidade.
Caso descubram algum caso em que ela não se aplica, uma lei mais
completa passa a substituí-la.
Até hoje, não conhecemos nenhuma situação em que haja
verdadeiramente perda ou ganho de energia, mas apenas
transformações entre as várias modalidades que existem.
Dessa forma, podemos enunciar a seguinte lei: a quantidade total de
energia do Universo é constante.
Lei da Conservação da Energia
Às vezes, tal afirmação pode parecer estranha, mas, para
mostrarmos a validade dessa lei, vamos analisar alguns
exemplos:
a) Quando um veículo é freado bruscamente, podemos ter a
impressão de que há perda de energia, pois ocorre
diminuição de energia cinética – se analisarmos esse caso
mais a fundo, perceberemos que, durante a frenagem, as
pastilhas e o disco de freio ficam superaquecidos e sons
podem ser ouvidos.
A conclusão é que energia mecânica é transformada em
energia térmica e sonora, de forma que o valor total de energia
não sofre alteração.
Lei da Conservação da Energia
b) Quando um paraquedas é aberto e o saltador
adquire velocidade constante, podemos ter a
impressão de que há perda de energia, pois
ocorre diminuição de energia potencial – mais
uma vez, uma parcela da energia mecânica dos
corpos envolvidos é dissipada, ou seja,
transformada em outras modalidades.
Podemos perceber isso se pensarmos que, durante
a queda, o atrito do paraquedas com o ar provoca
muito barulho e um certo aquecimento dele, do ar e
do paraquedista.
Lei da Conservação da Energia
c) Quando riscamos um fósforo, os átomos contidos na
cabeça dele se combinam ao oxigênio do ar, formando
novas moléculas.
Se pudéssemos medir e comparar a quantidade total de
energia antes e após a combustão, perceberíamos que,
depois dela, o valor obtido seria maior – ocorre que, em
reações químicas que liberam energia, as quantidades totais
de massa antes e depois de elas ocorrerem também não são
iguais.
Se fôssemos capazes de mensurar, notaríamos que, após elas
se concretizarem, a massa total dos produtos seria
ligeiramente menor.
Aparentemente, teríamos uma dupla violação de leis
(conservação da massa e da energia), mas, de acordo com a
equação E = m . c2, como energia e massa são “duas faces da
mesma moeda”, o aumento de uma delas explica a diminuição
da outra.
Lei da Conservação da Energia
Esses são apenas alguns exemplos, mas,
até que algum caso contrarie que energia
não pode ser criada, nem destruída,
continua sendo válida a Lei da Conservação
da Energia.
Lei da Conservação da Energia
Resolução de Atividades
Página 26 e 27
Sistemas conservativos
Já vimos que, em sistemas dissipativos, ocorre diminuição da
energia mecânica pelo fato de o trabalho das forças não
conservativas ser resistente, ou seja, negativo.
Assim, como (τFñcons = EMf - EMi) : como EMf – EMi < 0 , então EMf
< EMi.
Partindo dessa ideia, o que deveria ocorrer para que um
sistema pudesse ser classificado como conservativo?
Obviamente, algumas pessoas poderiam responder que a
denominação conservativo se refere ao fato de a energia
mecânica se conservar.
Assim, para termos um sistema conservativo, deveríamos ter
EMf = EMi.
Apesar de essa resposta parecer extremamente lógica, ela não
responde à pergunta, pois confunde a consequência de um
fenômeno com sua respectiva causa.
Sistemas conservativos
Para entendermos melhor isso, vamos fazer
a demonstração de um importante teorema
da Mecânica.
Teorema da Conservação da Energia
Mecânica
Iniciando nossa demonstração pelo Teorema da Energia
Mecânica, temos (τFñcons = EMf - EMi).
Se fizermos a suposição de que é possível termos uma
situação em que o trabalho das forças não conservativas é
nulo τFñcons = 0, então poderemos escrever que 0 = EMf - EMi, ou
seja, EMf = EMi.
Assim, a causa de um sistema ser conservativo é termos o
trabalho das forças não conservativas nulo.
A consequência de termos um sistema desse tipo é ocorrer
conservação da energia mecânica do sistema.
Diferente do que pode parecer, num sistema conservativo,
podem atuar forças não conservativas.
A única condição é que o trabalho total realizado por elas seja
igual a zero.
Teorema da Conservação da Energia
Mecânica
Como exemplo, vamos analisar
a situação a seguir, em que um
corpo escorrega por um plano
inclinado perfeitamente liso:
Nesse caso, apenas duas
forças atuam sobre esse corpo:
Normal: força não conservativa.
Por ser perpendicular ao
deslocamento do corpo, não
realiza trabalho.
Peso: força conservativa. Por
formar ângulo agudo (menor
que 90º) com o deslocamento
do corpo, realiza trabalho motor
durante toda a descida.
Nesse caso, apesar de uma
força não conservativa (normal)
agir sobre o corpo que
escorrega, o sistema continua
sendo classificado como
conservativo. Assim EMf = EMi
Moto-perpétuo
Para conseguir representar
a situação fisicamente
impossível da ilustração
anterior, Escher fez um
desenho em que as colunas
que sustentam o circuito da
água partem ou chegam a
posições completamente
absurdas.
É possível desenhar, mas
não construir essa
edificação.
Moto-perpétuo
Se existisse uma construção
como a proposta por
Escher, a água poderia se
movimentar indefinidamente
e ainda colocaria em
movimento uma rodad’água.
Nesse caso, essa “máquina
fantástica” seria chamada
de perpetuum mobile ou
moto-perpétuo (moto, de
movimento, e perpétuo por
ser eterno, de duração
indefinida).
Moto-perpétuo
Hoje, sabemos da impossibilidade de se construir
um moto-perpétuo, ou seja, uma máquina que se
autoalimenta da própria energia, mantendo-se
continuamente em movimento ou até produzindo
energia por meio do nada (isso contraria a Lei da
Conservação da Energia).
Segundo Newton, “os que buscam o moto-perpétuo
estão tentando obter alguma coisa a partir do nada”.
Moto-perpétuo
No entanto, durante muitos e muitos séculos,
diversos cientistas dedicaram boa parte de
suas vidas tentando inventar algo assim.
A sequência a seguir representa um
exemplo simples e interessante:
Moto-perpétuo
Moto-perpétuo
Na sequência, a bolinha metálica tende a subir devido à
atração magnética exercida pelo ímã colocado no alto do
experimento.
Pouco antes de atingir o ponto mais alto da rampa, em função
da presença de um orifício no plano inclinado, ela cai e desce
pela superfície curvilínea mostrada, sendo guiada diretamente
a outro orifício.
Após atravessá-lo, essa bolinha retorna à rampa e o ciclo
recomeça, ou melhor, recomeçaria (se tudo o que foi descrito
pudesse realmente acontecer).
Como podemos perceber que esse suposto moto-perpétuo não
funciona?
Moto-perpétuo
Ocorre que, se a força magnética for suficientemente intensa a
ponto de puxar a bolinha metálica até o ponto mais alto da
rampa, ela será suficientemente intensa também para jamais
deixar essa bolinha cair.
Assim, logo que esse experimento inicia, a bolinha começa a
subir e gruda no ímã, cessando de vez seu movimento.
Como todos os casos de supostos motos-perpétuos
apresentados até hoje, esse também apresenta alguma falha
ou fica sujeito a forças dissipativas, ocasionando a parada
repentina ou gradual da máquina criada.
Resolução de Atividades
Página 29 e 30