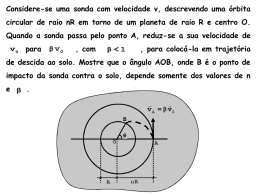
Dinâmica do Movimento Circular
1. (Unesp 2014) Em um show de patinação no gelo, duas
garotas de massas iguais giram em movimento circular
uniforme em torno de uma haste vertical fixa,
perpendicular ao plano horizontal. Duas fitas, F1 e F2,
inextensíveis, de massas desprezíveis e mantidas na
horizontal, ligam uma garota à outra, e uma delas à haste.
Enquanto as garotas patinam, as fitas, a haste e os centros
de massa das garotas mantêm-se num mesmo plano
perpendicular ao piso plano e horizontal
Considerando as informações indicadas na figura, que o
módulo da força de tração na fita F1 é igual a 120 N e
desprezando o atrito e a resistência do ar, é correto afirmar
que o módulo da força de tração, em newtons, na fita F2 é
igual a
a) 120.
b) 240.
c) 60.
d) 210.
e) 180.
2. (Fuvest 2014) Há um ponto no segmento de reta unindo
o Sol à Terra, denominado “Ponto de Lagrange L1”. Um
satélite artificial colocado nesse ponto, em órbita ao redor
do Sol, permanecerá sempre na mesma posição relativa
entre o Sol e a Terra.
Nessa situação, ilustrada na figura acima, a velocidade
angular orbital ωA do satélite em torno do Sol será igual à
Note e adote:
1 ano ≈ 3,14 × 107 s.
O módulo da força gravitacional F entre dois corpos de
massas M1 e M2, sendo r a distância entre eles, é dado
2
por F = G M1 M2/r .
Considere as órbitas circulares.
3. (Fuvest 2014) Duas pequenas esferas, cada uma com
massa de 0,2 kg, estão presas nas extremidades de uma
haste rígida, de 10 cm de comprimento, cujo ponto médio
está fixo no eixo de um motor que fornece 4 W de potência
mecânica. A figura abaixo ilustra o sistema.
No instante t = 0, o motor é ligado e o sistema, inicialmente
em repouso, passa a girar em torno do eixo. Determine
a) a energia cinética total E das esferas em t = 5 s;
b) a velocidade angular ω de cada esfera em t = 5 s;
c) a intensidade F da força entre cada esfera e a haste, em t
= 5 s;
d) a aceleração angular média α de cada esfera, entre t = 0
e t = 5 s.
Note e adote:
As massas da haste e do eixo do motor devem ser
ignoradas.
Não atuam forças dissipativas no sistema.
4. (Epcar (Afa) 2013) Em um local onde a aceleração da
gravidade vale g, uma partícula move-se sem atrito sobre
uma pista circular que, por sua vez, possui uma inclinação
θ. Essa partícula está presa a um poste central, por meio
de um fio ideal de comprimento ℓ que, através de uma
articulação, pode girar livremente em torno do poste. O fio
é mantido paralelo à superfície da pista, conforme figura
abaixo.
da Terra, ωT . Para essa condição, determine
a) ωT  em função da constante gravitacional G, da massa
MS do Sol e da distância R entre a Terra e o Sol;
b) o valor de ωA em rad/s;
c) a expressão do módulo Fr da força gravitacional
resultante que age sobre o satélite, em função de G, MS
,MT, m, R e d, sendo MT e m, respectivamente, as massas
da Terra e do satélite e d a distância entre a Terra e o
satélite.
www.soexatas.com
Ao girar com uma determinada velocidade constante, a
partícula fica “flutuando” sobre a superfície inclinada da
pista, ou seja, a partícula fica na iminência de perder o
contato com a pista e, além disso, descreve uma trajetória
circular com centro em C, também indicado na figura.
Página 1
Nessas condições, a velocidade linear da partícula deve ser
igual a
a)
3 
 gℓ 
2 
b)
( gℓ )
c)
d)
3 gℓ
4
2
( gℓ )
5. (Unesp 2013) A figura representa, de forma simplificada,
o autódromo de Tarumã, localizado na cidade de Viamão,
na Grande Porto Alegre. Em um evento comemorativo, três
veículos de diferentes categorias do automobilismo, um
kart (K), um fórmula 1 (F) e um stock-car (S), passam por
diferentes curvas do circuito, com velocidades escalares
iguais e constantes.
Ao passar pelo ponto mais baixo da trajetória a força
exercida pelo banco da aeronave sobre o piloto que a
comanda é:
a) igual ao peso do piloto.
b) maior que o peso do piloto.
c) menor que o peso do piloto.
d) nula.
e) duas vezes maior do que o peso do piloto.
7. (Uff 2012) Uma criança se balança em um balanço, como
representado esquematicamente na figura a seguir.
Assinale a alternativa que melhor representa a aceleração
a da criança no instante em que ela passa pelo ponto mais
baixo de sua trajetória.
a)
b)
c)
d)
As tabelas 1 e 2 indicam, respectivamente e de forma
comparativa, as massas de cada veículo e os raios de
curvatura das curvas representadas na figura, nas posições
onde se encontram os veículos.
TABELA 1
Veículo
Massa
kart
M
fórmula 1
3M
stock-car
6M
TABELA 2
Curva
Raio
Tala Larga
2R
do Laço
R
Um
3R
Sendo FK, FF e FS os módulos das forças resultantes
centrípetas que atuam em cada um dos veículos nas
posições em que eles se encontram na figura, é correto
afirmar que
a) FS < FK < FF.
b) FK < FS < FF.
c) FK < FF < FS.
d) FF < FS < FK.
e) FS < FF < FK.
6. (Ibmecrj 2013) Um avião de acrobacias descreve a
seguinte trajetória descrita na figura abaixo:
e)
8. (Fuvest 2012) Nina e José estão sentados em cadeiras,
diametralmente opostas, de uma roda gigante que gira com
velocidade angular constante. Num certo momento, Nina
se encontra no ponto mais alto do percurso e José, no mais
baixo; após 15 s, antes de a roda completar uma volta, suas
posições estão invertidas. A roda gigante tem raio R = 20 m
e as massas de Nina e José são, respectivamente, MN = 60
kg e MJ = 70 kg. Calcule
a) o módulo v da velocidade linear das cadeiras da roda
gigante;
b) o módulo aR da aceleração radial de Nina e de José;
c) os módulos NN e NJ das forças normais que as cadeiras
exercem, respectivamente, sobre Nina e sobre José no
instante em que Nina se encontra no ponto mais alto do
percurso e José, no mais baixo.
NOTE E ADOTE
π=3
2
Aceleração da gravidade g = 10 m/s
TEXTO PARA A PRÓXIMA QUESTÃO:
Use quando necessário:
- Aceleração da gravidade g = 10m / s2 ; Densidade da
água ρ = 1,0g / cm3 = 1000kg / m3
- Velocidade da luz no vácuo c = 3,0 × 108 m / s
www.soexatas.com
Página 2
- Constante de Planck
−34
h = 6,63 × 10 J × s = 4,14 × 10
- Constante π = 3,14
−15
eV × s;
9. (Ufjf 2012) A figura a seguir mostra um escorregador na
forma de um semicírculo de raio R = 5,0 m. Um garoto
escorrega do topo (ponto A) até uma altura h (ponto C)
abaixo do topo, onde perde o contato com o escorregador.
Nessa posição, a reta que passa pelo ponto C e pelo centro
O do círculo faz um ângulo θ com a reta normal à base do
semicírculo. A figura mostra também um ponto B que está
entre o ponto A e o ponto C. Desprezando os atritos ou
quaisquer perdas de energia:
a) faça o diagrama das forças que atuam sobre o garoto no
ponto B e identifique cada uma das forças.
b) calcule a altura h no momento em que o garoto perde o
contato com o escorregador.
c) calcule o valor da velocidade tangencial na situação do
item (b).
10. (Cesgranrio 2011) Uma esfera de massa igual a 3 kg
está amarrada a um fio inextensível e de massa desprezível.
A esfera gira com velocidade constante em módulo igual a
11. (Epcar (Afa) 2011) Um garoto, que se encontra em
repouso, faz girar, com velocidade constante, uma pedra de
massa m presa a um fio ideal. Descrevendo uma trajetória
circular de raio R num plano vertical, essa pedra dá diversas
voltas, até que, em um dado instante, o fio arrebenta e ela
é lançada horizontalmente, conforme ilustra a figura a
seguir.
Sujeita apenas à aceleração da gravidade g, a pedra passou,
então, a descrever uma trajetória parabólica, percorrendo
uma distância horizontal x equivalente a 4R.
A tração experimentada pelo fio toda vez que a pedra
passava pelo ponto onde ele se rompeu era igual a
a) mg
b) 2 mg
c) 3 mg
d) 4 mg
12. (Ufla 2010) Um corpo desliza sem atrito ao longo de
uma trajetória circular no plano vertical (looping), passando
pelos pontos, 1,2,3 e 4, conforme figura a seguir.
Considerando que o corpo não perde contato com a
superfície, em momento algum, é correto afirmar que os
diagramas que melhor representam as direções e sentidos
das forças que agem sobre o corpo nos pontos 1,2,3 e 4 são
apresentados na alternativa:
4 6
m/s, formando um cone circular imaginário,
15
conforme a figura abaixo.
a)
O fio permanece esticado durante todo o movimento,
fazendo um mesmo ângulo α com a vertical, cuja tangente
é 8/15. A componente horizontal da tração no fio vale 16 N
e é a força centrípeta responsável pelo giro da esfera. O
3
volume do cone imaginário, em cm , é
a) 280π
b) 320π
c) 600π
d) 960π
e) 1800π
www.soexatas.com
b)
c)
d)
Página 3
13. (Ufla 2010) Uma esfera de massa 500 gramas desliza
em uma canaleta circular de raio 80 cm, conforme a figura
a seguir, completamente livre de atrito, sendo abandonada
2
na posição P1. Considerando g = 10 m/s , é correto afirmar
que essa esfera, ao passar pelo ponto P2 mais baixo da
canaleta, sofre uma força normal de intensidade:
intensidade da força de reação que a pista aplica no veículo
2
é: (Adote g = 10m/s ).
a) 231512 N
b) 215360 N
c) 1800 N
d) 25800 N
e) 24000 N
a) 5N
b) 20N
c) 15N
d) π N
14. (Unesp 2010) Curvas com ligeiras inclinações em
circuitos automobilísticos são indicadas para aumentar a
segurança do carro a altas velocidades, como, por exemplo,
no Talladega Superspeedway, um circuito utilizado para
corridas promovidas pela NASCAR (National Association for
Stock Car Auto Racing). Considere um carro como sendo um
ponto material percorrendo uma pista circular, de centro C,
inclinada de um ângulo α e com raio R, constantes, como
mostra a figura, que apresenta a frente do carro em um dos
trechos da pista.
16. (Ufop 2010) Uma estação espacial é projetada como
sendo um cilindro de raio r, que gira em seu eixo com
velocidade angular constante ω, de modo a produzir uma
2
sensação de gravidade de 1g = 9,8 m/s nos pés de uma
pessoa que está no interior da estação.
Admitindo-se que os seus habitantes têm uma altura média
de h = 2 m, qual deve ser o raio mínimo r da estação, de
modo que a variação da gravidade sentida entre os pés e a
cabeça seja inferior a 1% de g?
17. (Ita 2009)
A partir do repouso, um carrinho de montanha russa desliza
°
de uma altura H = 20 3 m sobre uma rampa de 60 de
inclinação e corre 20 m num trecho horizontal antes de
chegar a um loop circular, de pista sem atrito.
Se a velocidade do carro tem módulo constante, é correto
afirmar que o carro
a) não possui aceleração vetorial.
b) possui aceleração com módulo variável, direção radial e
no sentido para o ponto C.
c) possui aceleração com módulo variável e tangente à
trajetória circular.
d) possui aceleração com módulo constante, direção radial
e no sentido para o ponto C.
e) possui aceleração com módulo constante e tangente à
trajetória circular.
15. (Pucsp 2010) Um automóvel de massa 800 kg, dirigido
por um motorista de massa igual a 60 kg, passa pela parte
mais baixa de uma depressão de raio = 20 m com
velocidade escalar de 72 km/h. Nesse momento, a
www.soexatas.com
Sabendo que o coeficiente de atrito da rampa e do plano
1
horizontal é , assinale o valor do raio máximo que pode
2
ter esse loop para que o carrinho faça todo o percurso sem
perder o contato com a sua pista.
a) R = 8 3 m
b) R = 4( 3 - 1)m
c) R = 8( 3 - 1)m
d) R = 4(2 3 -1)m
Página 4
e) R = 40
(
)m
d) tem sentido contrário ao da velocidade.
3 −1
3
18. (Ita 2009) Considere um pêndulo simples de
comprimento L e massa m abandonado da horizontal.
Então, para que não
ão arrebente, o fio do pêndulo deve ter
uma resistência à tração pelo menos igual a:
a) mg.
b) 2 mg.
c) 3 mg.
d) 4 mg.
e) 5 mg.
19. (Pucrj 2009) Um brinquedo de parque de diversões
consiste (veja as figuras a seguir) de um eixo vertical
vert
girante, duas cabines e um suporte para os cabos que ligam
o eixo às cabines. O suporte é uma forte barra horizontal de
aço, de L = 8,0 m de comprimento, colocada de modo
simétrico para poder sustentar as cabines. Cada cabo mede
d = 10 m.
Quando as pessoas
ssoas entram nas cabines, o eixo se põe a
girar e as cabines se inclinam formando um ângulo ? com a
vertical. O movimento das cabines é circular uniforme,
ambos de raio R. Considere a massa total da cabine e
passageiro como M = 1000 kg.
°
O módulo da aceleração vetorial dessa partícula nesse
2
trecho, em m/s , é
a) zero.
b) 1,5.
c) 3,0.
d) 4,5.
e) impossível de ser calculado.
22. (Ita 2007) Um corpo de massa m e velocidade V0 a uma
altura h desliza sem atrito sobre uma pista que termina em
forma de semicircunferência de raio r, conforme indicado
na figura. Determine a razão entre as coordenadas x e y do
ponto P na semicircunferência, onde o corpo perde o
contato com a pista. Considere a aceleração da gravidade g.
2
Suponha que θ = 30 . Considere g = 10 m/s para a
aceleração gravitacional e despreze todos os efeitos de
resistência do ar.
a) Desenhe na figura anterior o raio R de rotação, para a
trajetória da cabine do lado direito, e calcule seu valor.
b) Desenhe na figura anterior ass forças agindo sobre a
cabine do lado esquerdo. Qual a direção e o sentido da
força resultante Fr sobre esta cabine?
c) Sabendo que as forças verticais sobre a cabine se
cancelam, calcule a tensão no cabo que sustenta a cabine.
d) Qual o valor da força centrípeta
ntrípeta agindo sobre a cabine?
20. (Pucmg 2009) Um objeto percorre uma circunferência
em movimento circular uniforme. A força resultante sobre
esse objeto:
a) é nula, porque não há aceleração.
b) é dirigida para o centro.
c) é tangente à velocidade do objeto.
www.soexatas.com
21. (Unifesp 2007) A trajetória de uma partícula,
representada na figura, é um arco de circunferência de raio
r = 2,0 m, percorrido com velocidade de módulo constante,
v = 3,0 m/s.
23. (Ufjf 2007) Em alguns tipos de corridas de carros, os
circuitos podem ser descritos com boa aproximação como
sendo compostos de duas semicircurferências de raios R =
100 m e duas retas de comprimentos L = 900 m, como
mostra a figura a seguir. Suponha que um dos pilotos faz
com que o carro por ele pilotado percorra o circuito como
descrito a seguir. O carro faz as curvas de raio R, com o
módulo da velocidade constante, vR= 60 m/s, e tão logo sai
das curvas, imprime uma aceleração constante até atingir
1
das retas, permanecendo com uma velocidade
3
constante de 100 m/s num outro trecho. Desacelera com
aceleração constante no último
1
da reta, chegando
3
Página 5
novamente a curva com a velocidade vR. Para este carro,
calcule:
25. (Fgv 2007) No momento em que o braseiro atinge o
ponto mais baixo de sua trajetória, considerando que ele
descreve um movimento no sentido anti-horário e que a
trajetória é percorrida com velocidade constante, dos
vetores indicados, aquele que mais se aproxima da direção
e sentido da força resultante sobre a lata é
a) a aceleração centrípeta sofrida pelo carro nas curvas, e a
razão entre esta aceleração e a aceleração gravitacional g
2
(considere g = 10 m/s ).
b) o tempo total gasto pelo carro para dar uma volta no
circuito completo.
24. (Pucsp 2007)
26. (Fgv 2007)
A figura representa em plano vertical um trecho dos trilhos
de uma montanha russa na qual um carrinho está prestes a
realizar uma curva. Despreze atritos, considere a massa
total dos ocupantes e do carrinho igual a 500 kg e a máxima
velocidade com que o carrinho consegue realizar a curva
sem perder contato com os trilhos igual a 36 km/h. O raio
da curva, considerada circular, é, em metros, igual a
a) 3,6
b) 18
c) 1,0
d) 6,0
e) 10
Mantendo o movimento circular de raio 80 cm, a menor
velocidade que a lata deve possuir no ponto mais alto de
sua trajetória para que o carvão não caia da lata é, em m/s,
a)
2
b) 2
c) 2 2
d) 4
e) 4 2
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Vendedores aproveitam-se da morosidade do trânsito para
vender amendoins, mantidos sempre aquecidos em uma
bandeja perfurada encaixada no topo de um balde de
alumínio; dentro do balde, uma lata de leite em pó, vazada
por cortes laterais, contém carvão em brasa (figura 1).
Quando o carvão está por se acabar, nova quantidade é
reposta. A lata de leite é enganchada a uma haste de metal
(figura 2) e o conjunto é girado vigorosamente sob um
plano vertical por alguns segundos (figura 3), reavivando a
chama.
Dados:
π = 3,1
2
g = 10 m/s
www.soexatas.com
27. (Ita 2006) Uma estação espacial em forma de um
toroide, de raio interno R1, e externo R2, gira, com período
P, em torno do seu eixo central, numa região de gravidade
nula. O astronauta sente que seu "peso" aumenta de 20%,
quando corre com velocidade constante v no interior
desta estação, ao longo de sua maior circunferência,
conforme mostra a figura. Assinale a expressão que indica o
módulo dessa velocidade.
Página 6
a) I
b) II
c) III
d) II e III
e) I e II
a) v =
 6
 2 πR 2
− 1


 5
 P

5  2 πR 2
b) v =  1 −


6  P

 5
 2 πR 2
+ 1


 6
 P
 5  2 πR 2
d) v =  + 1
6  P
 6  2 πR 2
e) v =  − 1
5  P
c) v =
29. (Pucsp 2006) Um automóvel percorre uma curva
circular e horizontal de raio 50 m a 54 km/h. Adote g = 10
2
m/s . O mínimo coeficiente de atrito estático entre o
asfalto e os pneus que permite a esse automóvel fazer a
curva sem derrapar é
a) 0,25
b) 0,27
c) 0,45
d) 0,50
e) 0,54
30. (Unicamp 2006) Um pêndulo cônico é formado por um
fio de massa desprezível
ezível e comprimento L = 1,25 m, que
suporta uma massa m = 0,5 kg na sua extremidade inferior.
A extremidade superior do fio é presa ao teto, conforme
ilustra a figura a seguir. Quando o pêndulo oscila, a massa
m executa um movimento circular uniforme num plano
horizontal, e o ângulo que o fio forma com a vertical é q =
°
60 .
a) Qual é a tensão no fio?
b) Qual é a velocidade angular da massa? Se for necessário,
°
°
use: sen 60 = 0,87, cos 60 = 0,5.
28. (Pucsp 2006) Durante umaa apresentação da
Esquadrilha da Fumaça, um dos aviões descreve a trajetória
circular da figura, mantendo o módulo de sua velocidade
linear sempre constante.
31. (Ufmg 2006) Durante uma aula de Física, o Professor
Raimundo
aimundo faz uma demonstração com um pêndulo cônico.
Esse pêndulo consiste em uma pequena esfera pendurada
na extremidade de um fio, como mostrado nesta figura:
Sobre o descrito são feitas as seguintes afirmações:
I - A força com a qual o piloto comprime o assento do avião
varia enquanto ele percorre a trajetória descrita.
II - O trabalho realizado pela força centrípeta que age sobre
o avião é nulo em qualquer ponto da trajetória descrita.
III - Entre os pontos A e B da trajetória descrita pelo avião
não há impulso devido à ação da força centrípeta.
Somente está correto o que se lê em
www.soexatas.com
Nesse pêndulo, a esfera descreve um movimento circular
com velocidade de módulo constante, em um plano
horizontal, situado a 1,6 m abaixo do ponto em que o fio
está preso ao teto. A massa da esfera é 0,40 kg, o raio de
sua trajetória é 1,2 m e o comprimento do fio é 2,0 m.
Considere a massa do fio desprezível. Despreze, também,
qualquer tipo de atrito.
Página 7
Com base nessas informações:
a) DESENHE e NOMEIE, na figura, as forças que atuam na
esfera. RESPONDA:
Quais são os agentes que exercem essas forças?
b) CALCULE a tensão no fio.
c) CALCULE a energia cinética da esfera.
32. (Unifesp 2003) Antes de Newton expor sua teoria sobre
a força da gravidade, defensores da teoria de que a Terra se
encontrava imóvel no centro do Universo alegavam que, se
a Terra possuísse movimento de rotação, sua velocidade
deveria ser muito alta e, nesse caso, os objetos sobre ela
deveriam ser arremessados para fora de sua superfície, a
menos que uma força muito grande os mantivesse ligados à
6
Terra. Considerando o raio da Terra de 7 × 10 m, o seu
período
4
2
de rotação de 9 × 10 s e π = 10, a força mínima capaz de
manter um corpo de massa 90kg em repouso sobre a
superfície da Terra, num ponto sobre a linha do Equador,
vale, aproximadamente,
a) 3 N.
b) 10 N.
c) 120 N.
d) 450 N.
e) 900 N.
33. (Cesgranrio 2002) Um brinquedo comum em parques
de diversões é o "bicho-da-seda", que consiste em um carro
com cinco bancos para duas pessoas cada e que descreve
sobre trilhos, em alta velocidade, uma trajetória circular.
Suponha que haja cinco adultos, cada um deles
acompanhado de uma criança, e que, em cada banco do
carro, devam acomodar-se uma criança e o seu
responsável.
Para que, com o movimento, o adulto não prense a criança
contra a lateral do carro, é recomendável que o adulto
ocupe o assento mais ______________ do centro da
trajetória, pois o movimento os empurrará em sentido
______________ com uma força ______________
proporcional ao raio da trajetória.
Preenche correta e respectivamente as lacunas acima a
opção:
a) próximo - a esse centro - diretamente.
b) próximo - a esse centro - inversamente.
c) afastado - a esse centro - diretamente.
d) afastado - oposto a esse centro - diretamente.
e) afastado - oposto a esse centro - inversamente.
34. (Ufrj 2002) Pistas com curvas de piso inclinado são
projetadas para permitir que um automóvel possa
descrever uma curva com mais segurança, reduzindo as
forças de atrito da estrada sobre ele. Para simplificar,
considere o automóvel como um ponto material.
www.soexatas.com
a) Suponha a situação mostrada na figura anterior, onde se
representa um automóvel descrevendo uma curva de raio
R, com velocidade V tal que a estrada não exerça forças de
atrito sobre o automóvel. Calcule o ângulo α de inclinação
da curva, em função da aceleração da gravidade g e de V.
b) Suponha agora que o automóvel faça a curva de raio R,
com uma velocidade maior do que V. Faça um diagrama
representando por setas as forças que atuam sobre o
automóvel nessa situação.
35. (Uerj 2001) O globo da morte apresenta um
motociclista percorrendo uma circunferência em alta
velocidade.
Nesse circo, o raio da circunferência é igual a 4,0m.
Observe o esquema a seguir:
O módulo da velocidade da moto no ponto B é 12m/s e o
sistema moto-piloto tem massa igual a 160kg.
Determine a componente radial da resultante das forças
sobre o globo em B.
36. (Ufrj 2000) A figura mostra o perfil de um trilho vertical
JKLM cujo trecho KLM é circular de centro em C e raio R.
Um bloco de pequenas dimensões é abandonado a uma
altura h=R/2 acima do plano horizontal que contém o
centro C e passa a deslizar sobre o trilho com atrito
Página 8
desprezível.
a) Determine a direção e o sentido da velocidade v do
bloco no instante em que ele passa pelo ponto L e calcule
seu módulo em função de R e da aceleração da gravidade g.
b) Determine a direção e o sentido da resultante F das
forças que atuam sobre o bloco no instante em que ele
passa pelo ponto L (informando o ângulo que ela forma
com a horizontal) e calcule seu módulo em função da massa
m do bloco e da aceleração da gravidade g.
www.soexatas.com
Página 9