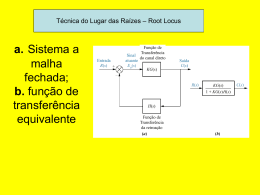
PTC2433 - TEORIA DAS COMUNICAÇÕES II - 23/08/2015 - PJEJ
RESOLUÇÃO PARCIAL DA TERCEIRA LISTA DE EXERCÍCIOS
Q1) No projeto de códigos corretores de erro se o comprimento do código ou o número de bits de informação não puderem ser achados de
forma adequada pode-se reduzir um código para atingir esse objetivo. Assim, dado um código de bloco cíclico e sistemático (n,k) pode-se a
partir deste construir um outro código de bloco (n-p, k-p) observando que das 2k palavras de código originais 2k-p tem p zeros nas primeiras
posições. Esse novo código é ainda sistemático, mas não cíclico, e tem as mesmas propriedades de distância do código original. Assim, por
exemplo, dado um código (31,26) a sua redução de três dígitos leva-nos ao código (28,23) com a mesma capacidade de correção anterior.
Mostre como se efetua a codificação, e decodificação, desse novo código a partir do polinômio g(x) original. Em que condições esse código
reduzido será cíclico?
Resolução
A figura abaixo ilustra o esquema de redução proposto que consiste em manter apenas as informações que em sua forma original iniciavam
com p zeros (em número total de 2k-p). Os novos dados, de comprimento k-p, agora sem os p zeros iniciais constituem a nova informação e os
(n-p) dígitos da palavra código correspondente (obtida da original pela supressão dos p zeros iniciais, pois o código original era sistemático)
constituem o novo código.
Evidentemente, as distâncias entre palavras códigos são as mesmas já que apenas zeros foram eliminados para formar as novas palavras
código. Assim a capacidade de correção é a mesma do código original.
k
p
0
n
k-p
dados
do código
reduzido
p
0
n-p
palavras
código
reduzidas
k-p
2
k
2
O processo de codificação é o mesmo pois para o código original:
c(x)=xn-k d(x)+Rem(xn-kd(x)/g(x))
onde:
- d(x) é de grau (k-1) ou menor e portanto xn-k d(x) será de grau (n-1) ou menor, com seu termo de menor grau de grau (n-k);
- a segunda parcela é de grau (n-k-1) ou menor (determinado pelo grau de g(x));
- assim as duas parcelas se somam sem ter termos de mesmo grau em comum ("disjuntos").
Já para o código reduzido d(x) é de grau (k-p-1) e pode ser escrito como sendo o d(x) reduzido acrescido de p termos de maior grau com
coeficientes nulos e assim toda construção anterior se mantém. Assim para a codificação escreve-se:
c(x)=xn-k d(x)+Rem(xn-kd(x)/g(x)) com d(x) de grau (k-p-1) resultando num polinômio de grau (n-p-1), como esperado.
Para a decodificação basta observar que originalmente faz-se o cálculo da síndrome por s(x)=Rem(r(x)/g(x)). Assim, se os p primeiros dígitos
são nulos e não houve erro de transmissão nessas posições a síndrome calculada dessa mesma forma para o polinômio recebido r'(x), agora
de grau (n-p-1), será a mesma.
Finalmente, para que o código reduzido seja também um código cíclico g(x), que é originalmente um fator de (xn+1), deverá ser fator também
de (xn-p+1). Essa condição é necessária, mas não suficiente, como no próprio código original.
Q2) Seja um sistema de transmissão BPSK (Binary Phase Shift Keying). Compare o desempenho, em termos de probabilidade de erro de
palavra, de um sistema codificado com um código Hamming (15,11) e um não codificado. Considere λ=10 no caso não codificado. Qual a
hipótese necessária para essa comparação? Qual é a expansão de banda necessária para isso?
Resolução
No caso não codificado a probabilidade de erro de palavra é dada por Pw=kQ(sqr(2λ)) e é assim perfeitamente determinável (k=11 e λ=10).
Resultado Pw=11Q(4,47)=4,3x10-5
No caso codificado a probabilidade de erro de palavra é dada, aproximadamente, por Pw= Cn,t+1[Q(sqr(2kλ/n)]t+1, onde agora adicionalmente
usam-se os valores t=1 (pois esse código corrige um erro) e n=15. Resultado Pw= 105x[Q(3,83)]2=4,3x10-7 (100X menor).
A hipótese adotada nesse cálculo é de que as potências gastas nos dois sistemas (codificado e não) são iguais. Evidentemente, nesse caso a
banda expande-se por um fator n/k=1,36 devido à codificação (transmite-se mais informação no mesmo intervalo de tempo).
Q3) Esboce o diagrama de estados correspondente ao código convolucional abaixo representado. Neste código para cada bit de informação
são transmitidos três (N=3, k=1, n=3).
1
+
in
out
2
+
3
+
a) Considere a transmissão de 5 bits de informação 10110 seguidos de tantos zeros quantos forem necessários. Qual é a
seqüência de bits transmitida?
b) Qual a distância livre dfree deste código? E o ganho de codificação?
c) Faça uma decodificação hard da palavra recebida, antes do limitador, como:
r={-0,9; -0,7; -0,2; -0,8; 0,5; -0,6; 0,3; 0,3; 0,7; 0,8; -0,7; 0,7; -0,9; -0,8; -0,5; 1,0;-1,0; -1,0; 0,7; -0,8; 1,0} utilizando o decodificador
de Viterbi;
d) Refaça utilizando uma decodificação soft e comente seu resultado.
Resolução
Notação utilizada - estado: YX e N/nmp: entrada dígito N, saída dígitos nmp
1
+
in
out
2
+
3
+
Diagrama de estados correspondente:
0/000
00
0/011
1/111
1/100
10
01
0/101
0/110
1/010
11
1/001
Diagrama de treliças correspondente (não foi pedido):
000
00
011
111
01
entrada 0
101
100
entrada 1
10
010
110
11
dfree=7
001
Do diagrama de treliças sai imediatamente que, se entrada for 10110 e a isso acrescentarmos 2 zeros para levar o registrador para o estado
inicial, a saída correspondente será c = [111 101 100 010 110 011 000].
Seja agora a entrada
r={-0,9; -0,7; -0,2; -0,8; 0,5; -0,6; 0,3; 0,3; 0,7; 0,8; -0,7; 0,7; -0,9; -0,8; -0,5; 1,0;-1,0; -1,0; 0,7; -0,8; 1,0}
colocando o sinal na forma binária (após saída do limitador), para a decodificação hard
r={111 101 000 010 111 011 010}
O resto será concluído em classe.
Q4) O código de Golay (23,12) é um código cíclico com polinômio gerador dado por: g(x) = x11+x9+x7+x6+x5+x+1. Determine a
capacidade de correção deste código e palavra de código sistemática correspondente ao vetor de dados d=[000011110000].
Resolução
Este código pode corrigir até t=3 erros. Para obter a palavra de código solicitada faz-se c(x)=xn-kd(x) + Rem{ xn-kd(x)/g(x)} com
d(x)=x7+x6+x5+x4 e o g(x) dado, resultando:
c(x)= x18+x17+x16+x15 + Rem [(x18+x17+x16+x15) / ( x11+x9+x7+x6+x5+x+1)]= x18+x17+x16+x15 +x8+x6+x5+x4+x3+x2+1 (confira!)
e, portanto, a palavra de código correspondente é: r=[00001111000000101111101].
Q5) Deseja-se encontrar o caminho mais rápido para ir de Londres a Viena de barco ou trem. O diagrama a seguir mostra as
possibilidades existentes. Os números indicados são tempos de viagem em horas.
a) Usando o algoritmo de Viterbi, encontre a rota mais rápida entre Londres e Viena. Qual o tempo mínimo de viagem?
b) Repita o problema para determinação da rota mais demorada. Qual o tempo máximo de viagem?
Londres
x
10
Amsterdam
x
9
Munique
x
12
8
10
x
Paris
Respostas
a) Londres, Paris, Munique e Viena:27 horas
b) Londres, Amsterdam, Bruxelas e Viena: 29 horas.
9
7
8
x
Bruxelas
Viena
x