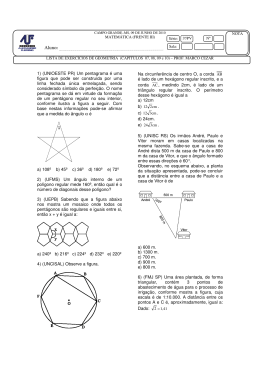
LISTA DE EXERCÍCIOS
(funções exponenciais e logarítmicas) – lista 02
PPRROOFF.. RRAAUURRYYSSOONN AALLVVEESS
01 - (UFG GO/2011) Quando um antibiótico é
ingerido, é absorvido pelo organismo e eliminado
gradativamente. Denotando por q0 a quantidade do
antibiótico no organismo do paciente num instante t0,
a função que descreve a quantidade, em um instante
posterior t, com t – t0 em horas, enquanto não houver
nova ingestão do antibiótico, é q(t) = 2–(t–t0)/2 q0 .
Havendo ingestão de antibiótico, soma-se a
quantidade ingerida à quantidade já presente no
organismo e, a partir daí, a quantidade decresce com
o tempo segundo a função acima. Considere o
tratamento de uma infecção com cápsulas de 500 mg
desse antibiótico, ingeridas em intervalos regulares,
sendo uma cápsula a cada x horas. Para conveniência
do paciente, x deve ser um número par de horas e,
para que o tratamento seja eficaz, a quantidade de
antibiótico no organismo do paciente deve ficar acima
de 60 mg durante todo o tratamento. Nestas
condições,
a) que quantidade do antibiótico da primeira cápsula,
em mg, restará no organismo duas horas após sua
ingestão?
b) Qual é o maior número par x (intervalo entre as
cápsulas) para que o tratamento seja eficaz?
02 - (UNIFOR CE/2011) Certa substância radioativa de
massa M0 (no instante t = 0) se desintegra (perde
massa) ao longo do tempo. Em cada instante t  0 em
segundos, a massa M(t) da substância restante é dada
por M(t) = M03–2t. O tempo transcorrido, em
segundos, para que a massa desintegrada da
substância seja dois terços da massa inicial M0 é:
a) 0,5 b) 1 c) 1,5 d) 2 e) 4
03 - (FEPECS DF/2011) Com base em uma pesquisa,
obteve-se o gráfico abaixo, que indica o crescimento
de uma cultura de bactérias ao longo de 12 meses
pela lei de formação representada pela função N(t) = k
 pt, onde k e p são constantes reais.
Nas condições dadas, o número de bactérias, após 4
meses, é:
a) 1800; b) 2400; c)3000; d) 3200; e) 3600.
04 - (UEPB/2011) A solução da equação
x  4 3x  8
2
=
3x  8
3
no conjunto R dos números reais é:
a) x = –2 b) x = 1 c) x = 0 d) x = 2 e) x = –1
2
05 - (FUVEST SP/2011) Seja f(x) = a + 2bx+c,em que a, b
e c são números reais. A imagem de f é a semirreta ]–
1, [ e o gráfico de f intercepta os eixos coordenados
nos pontos (1,0) e(0, –3/4). Então, o produto abc vale
a) 4 b) 2 c) 0 d) –2 e) –4
06 - (UFBA/2011) O gráfico representa uma projeção
do valor de mercado, v(t), de um imóvel, em função
do tempo t, contado a partir da data de conclusão de
sua construção, considerada como a data inicial t = 0.
O valor v(t) é expresso em milhares de reais, e o
tempo t, em anos.
Com base nesse gráfico, sobre o valor de mercado
projetado v(t), pode-se afirmar:
01. Aos dez anos de construído, o imóvel terá valor
máximo.
02. No vigésimo quinto ano de construído, o imóvel
terá um valor maior que o inicial.
04. Em alguma data, o valor do imóvel corresponderá
a 37,5% do seu valor inicial.
08. Ao completar vinte anos de construído, o imóvel
voltará a ter o mesmo valor inicial.

t 102
16. Se v(t) = 200·2 100 , então, ao completar trinta
anos de construído, o valor do imóvel será igual a um
oitavo do seu valor inicial.
07 - (FGV /2011) O serviço de compras via internet
tem aumentado cada vez mais. O gráfico ilustra a
venda anual de ebooks, livros digitais, em milhões de
dólares nos Estados Unidos.
Suponha que as vendas anuais em US$ milhões, possa
ser estimada por uma função como y = a.ekx, em que x
= 0 representa o ano 2002, x = 1, o ano 2003, e assim
por diante; e é o número de Euler. Assim, por
exemplo, em 2002 a venda foi de 7 milhões de
dólares. A partir de que ano a venda de livros digitais
nos Estados Unidos vai superar 840 milhões de
dólares? Use as seguintes aproximações para estes
logaritmos neperianos: ln 2 = 0,7; ln 3 = 1,1; ln 5 = 1,6
08 - (UERJ/2011) Para melhor estudar o Sol, os
astrônomos utilizam filtros de luz em seus
instrumentos de observação. Admita um filtro que
deixe passar
4
5
da intensidade da luz que nele incide.
Para reduzir essa intensidade a menos de 10% da
original, foi necessário utilizar n filtros. Considerando
log 2 = 0,301, o menor valor de n é igual a:
a) 9 b) 10 c) 11 d) 12
cobalto 60 sejam reduzidos, por desintegração, a
12,5g, em anos, é igual a
01. 20 02. 25 03. 30 04. 35 05. 40
10 - (UFCG PB/2010) Certa espécie de animal, com
população inicial de 200 indivíduos, vivendo em um
ambiente limitado, capaz de suportar no máximo 500
indivíduos,
é
modelada
pela
função
P(t)
onde a variável t é dada em anos. O
tempo necessário para a população atingir 60 % da
população máxima é
Obs: use a aproximação ln(4/9) = –0,8, onde lnx
representa o logritmo natural (ou neperiano) do
número real x.
a) 0,4 anos.
b) 0,2 anos.
c) 0,5 anos.
d) 0,1 anos.
e) 0,6 anos.
11 - (UFF RJ/2011) O índice de Theil, um indicador
usado para medir desigualdades econômicas de uma
 MA 
 , sendo

 MG 
população, é definido por T  ln
MA 
1 N
x  x   xN
 xi  1 2 N
N i 1
N
M G  N  x i  N x1  x 2    x N
i 1
e
,
respectivamente, as médias aritmética e geométrica
das rendas x1, x2, ..., xN (consideradas todas positivas e
medidas com uma mesma unidade monetária) de
cada um dos N indivíduos da população.
Com base nessas informações, assinale a afirmativa
incorreta.
a) T = ln(MA) – ln(MG).
 MA
 xi
b) ln 
c)
09 - (UNEB BA/2011) Cada elemento radioativo, seja
natural ou obtido artificialmente, se desintegra a uma
velocidade que lhe é característica. Meia-vida é o
tempo necessário para que a sua atividade seja
reduzida à metade da atividade inicial. O cobalto 60,
cuja radiação é muito utilizada em equipamentos de
radioterapia, tem meia-vida de 5 anos. Nessas
condições, o tempo necessário para que 800g de
100.000
200  300e 2 t

  0 para todo xi > 0, i = 1, ..., N.


xi
 MA
N
para todo i = 1, ..., N.
d) Se x1 = x2 = ... = xN, então T = 0.
e)
T
1 N  MA
 ln
N i 1  x i
 1   MA
   ln
 N  x

  1

M
  ln A

 x

 2
=
M

    ln A

 x

 N

 .


12 - (UPE/2011) Em química, define-se o pH de uma
solução pela relação pH = log(1/[H+]) onde [H+] é a
concentração do Hidrogênio em íons-grama por Litro
de solução. Chama-se de ácida uma solução cuja
concentração [H+] é estritamente maior que a mesma
concentração na água pura, na qual [H+] = 10–7 íonsgrama/L, e alcalina, uma solução na qual tal
concentração de íons H+ é menor que a da água.
Nessas condições, analise as afirmativas abaixo e
conclua.
00. Se uma solução A tem pH igual ao dobro de outra
solução B, então sua concentração de íons H+ é 100
vezes maior que a concentração da solução B.
01. Ao adicionar 10–5 íons-grama/L de íons H+ à água
pura, seu pH será alcalino.
02. Ao adicionar 10–6 íons-grama/L de íons H+ à água
pura, seu pH mudará de 7 para 6, sendo, portanto,
ácido.
03. Ao adicionar uma substância que remova 10–6
íons-grama/L de íons H+ da água pura, o pH da solução
resultante será alcalino.
04. A diferença de pH’s de duas soluções A e B cuja
concentração de íons H+ da solução A seja 100 vezes
maior que a da solução B é igual a 100 = 10
13 - (UNIFOR CE/2011) De uma torneira, que não foi
fechada corretamente, pingam n gotas a cada 30
segundos, onde n satisfaz à equação log4n = log23.
Considerando que o volume de cada gota é 0,2 ml,
podemos, então, concluir que, após uma hora, o
desperdício de água foi de:
a) 216 ml b) 250 ml c) 300 ml d) 314 ml e) 442 ml
14 - (FGV /2010) É comum as editoras enviarem
exemplares de livros didáticos novos aos professores,
para que estes possam analisá-los e, eventualmente,
usar como livro-texto nas suas salas de aula. O
gerente editorial de uma grande editora estima que,
se x exemplares de um novo livro de Cálculo forem
distribuídos gratuitamente aos professores, as vendas
no
primeiro
ano
serão
aproximadamente
x
exemplares, com x  0, em que
e = 2,718… é o número de Euler.
a) Mediante a função f(x), determine quantos livros
deverão ser vendidos, se a editora não distribuir
gratuitamente esse novo lançamento aos professores.
b) O gerente editorial planeja vender cerca de 12 000
livros de Cálculo no primeiro ano. Quantos livros a
editora
deverá
distribuir
aos
professores,
aproximadamente? Se necessário, use a aproximação:
ln3 = 1,1.
15 - (UCS RS/2010) Um modelo matemático, para
descrever a relação entre o crescimento de uma
grandeza y em função do tempo t, é y(t) = (n ab 3 )t,
em que a e b são constantes que dependem da
particular situação concreta modelada, e n denota o
logaritmo natural. Supondo que na = 2 e nb = 4,
qual é o valor de y quando t = 2?
a) 124 b) 128
c) 12 d) 24 e) 14
16 - (UCS RS/2009) Terremotos costumam ser
avaliados por sua magnitude e por sua intensidade. A
intensidade refere-se aos efeitos das vibrações na
superfície terrestre. A magnitude é o valor obtido na
escala Richter a partir da amplitude máxima das
vibrações do solo a 100 km do epicentro do
terremoto. A expressão M1  M 2  log
A1
A2
, em que log
denota o logaritmo decimal, relaciona as magnitudes
M1 e M2 de dois terremotos com as amplitudes A1 e A2
das ondas sísmicas geradas. Segundo essa expressão,
a relação entre as amplitudes A1 e A2 das ondas
geradas pelos terremotos de magnitudes 9 e 6,3
ocorridos, respectivamente, em 2004 na Indonésia e
em abril deste ano na Itália, é dada por
a) A1 = 270 A2.
b) A1 = 2,7 A2.
2,7
c) A1 = 10 A2.
d) A1 = 2,710 A2.
e) A2 = 2,7 A1.
17 - (UFMG/2009) Numa calculadora científica, ao se
digitar um número positivo qualquer e, em seguida, se
apertar a tecla log, aparece, no visor, o logaritmo
decimal do número inicialmente digitado. Digita-se o
número 10.000 nessa calculadora e, logo após,
aperta-se, N vezes, a tecla log, até aparecer um
número negativo no visor. Então, é CORRETO afirmar
que o número N é igual a
a) 2. b) 3.
c) 4.
d) 5.
f (x)  16000 12000 e 4000
18 - (ITA SP/1993) Um acidente de carro foi
presenciado por 1/65 da população de Votuporanga
(SP). O número de pessoas que soube do
acontecimento t horas após é dado por: f (t ) 
B
1 Ce kt
onde B é a população da cidade. Sabendo-se que 1/9
da população soube do acidente 3 horas após então o
tempo que passou até que 1/5 da população soubesse
da notícia foi de:
a) 4 horas b) 5 horas c) 6 horas
min e) 5 horas e 30 min
d) 5 horas e 24
e)
19 - (UEL PR/2001) O valor de um automóvel (em
unidades monetárias) sofre um depreciação de 4% ao
ano. Sabendo-se que o valor atual de um carro é de
40.000 unidades monetátiras, depois de quantos anos
o valor desse carro será de 16.000 unidades
monetárias? Use o valor 0,3 para log 2 e o valor 0,48
para log 3.
a) 3 b) 6 c) 10 d) 15 e) 23
TEXTO: 1 - Comum à questão: 20
Escalas logarítmicas são usadas para facilitar a
representação e a compreensão de grandezas que
apresentam intervalos de variação excessivamente
grandes. O pH, por exemplo, mede a acidez de uma
solução numa escala que vai de 0 a 14; caso fosse
utilizada diretamente a concentração do íon H+ para
fazer essa medida, teríamos uma escala bem pouco
prática, variando de 0,00000000000001 a 1. Suponha
que um economista, pensando nisso, tenha criado
uma medida da renda dos habitantes de um país
chamada Renda Comparativa (RC), definida por
 R
RC  log
 Ro

,


em que R é a renda, em dólares, de um
habitante desse país e Ro é o salário mínimo, em
dólares, praticado no país. (Considere que a notação
log indica logaritmo na base 10.)
20 - (IBMEC SP/2011) Dentre os gráficos abaixo,
aquele que melhor representa a Renda Comparativa
de um habitante desse país em função de sua renda,
em dólares, é
a)
c)
b)
d)
GABARITO:
1) Gab:
a) 250 mg
b) Para um intervalo x = t – to = 2k horas, tem-se
2-k 500 > 60  2-k >
6
50
 2k <
50
6
=
25
3
 8,33
então, como 23 = 8, o maior k inteiro, que satisfaz
esta desigualdade, é k = 3, que corresponde a um
intervalo de seis horas entre as cápsulas.
2) Gab: A
3) Gab: B
4) Gab: E
5) Gab: A
6) Gab: 29
7) Gab:
A partir de 2011.
8) Gab: C
9) Gab: 03
10) Gab: A
11) Gab: B
12) Gab: FFFVF
13) Gab: A
14) Gab:
a) 4000 exemplares
b)A editora deverá distribuir cerca de 4400 livros aos
professores.
15) Gab: E
16) Gab: C
17) Gab: B
18) Gab: A
19) Gab: E
20) Gab: D