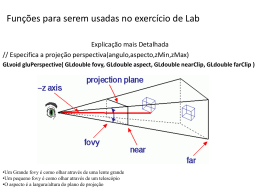
Programação em OpenGL
Daniel de Vasconcelos Campos
Tópicos
•
•
•
•
Problema proposto
Análise do problema
Possíveis abordagens
Técnica do ARCBALL
Tópicos
•
•
•
•
Problema proposto
Análise do problema
Possíveis abordagens
Técnica do ARCBALL
Problema Proposto:
Faça um programa que com um botão leia um
arquivo de cena do tipo do rt4 e, através das teclas,
, , mova a câmera para esquerda, direita, para
cima e para baixo, respectivamente. O usuário deve
também poder apontar com o mouse um objeto da
cena e com isto a câmera deve rotacionar de forma a
que o centro do objeto fique no eixo óptico da
câmera. Implemente esta rotação inicialmente de
qualquer maneira mas depois faça uma animação
onde o movimento da câmera seja o mais suave e
natural possível.
Tópicos
•
•
•
•
Problema proposto
Análise do problema
Possíveis abordagens
Técnica do ARCBALL
Análise do problema :
• O problema foi dividido em partes para que
fosse mais fácil resolvê-lo;
• Parte 1:
Faça um programa que com um botão leia um
arquivo de cena do tipo do rt4 e, através das
teclas, , , , mova a câmera para
esquerda, direita, para cima e para baixo,
respectivamente.
Tópicos
•
•
•
•
Problema proposto
Análise do problema
Possíveis abordagens para o 1⁰ subproblema
Técnica do ARCBALL
Glu Look At
void gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez,
GLdouble centerx, GLdouble centery, GLdouble centerz,
GLdouble upx, GLdouble upy, GLdouble upz);
Dados: eye, center, up (definem o sistema de coordenadas do olho)
Determine a matriz que leva do sistema de Coordenadas dos Objetos
para o sistema de Coordenadas do Olho
up
eye
center
eye
Coordenadas dos
objetos
Coordenadas do
olho
Análise do problema :
• Parte 2: (Não implementado)
– O usuário deve também poder apontar com o
mouse um objeto da cena e com isto a câmera
deve rotacionar de forma a que o centro do objeto
fique no eixo óptico da câmera. Implemente esta
rotação inicialmente de qualquer maneira mas
depois faça uma animação onde o movimento da
câmera seja o mais suave e natural possível.
Tópicos
•
•
•
•
Problema proposto
Análise do problema
Possíveis abordagens para o 2⁰ subproblema
Técnica do ARCBALL
Possíveis abordagens para o 2⁰
subproblema
• O próximo ponto seria utilizar a matriz que faz
a rotação xe ye ze para xw yw zw. Este passo é
melhor explicado no próximo slide.
Roda xe ye ze para xw yw zw
 xex
y
R   ex
 zex

0
yo ye
eye
zo
center
0
0
0

1
xez
yez
zez
0
ye , yo
ze
xe
xey
yey
zey
0
xo
ze , zo
xe , xo
A partir daí, a técnica do ARCBALL, seria
útil para que o usuário tenha a possibilidade
de enxergar o objeto do melhor ângulo de
interesse.
Tópicos
•
•
•
•
Problema proposto
Análise do problema
Possíveis abordagens para o 2⁰ subproblema
Técnica do ARCBALL
ARCBALL
• Transforma as coordenadas 2D do Mouse em
rotações.
• No modelo proposto por [2], possui a
importante propriedade de conservação das
rotações.
ARCBALL
• O procedimento mapeia as coordenadas dos
pontos inicial e final na esfera.
•
•
•
•
•
•
•
•
•
•
•
pt.x = (screen.x – center.x)/radius; // center : Centro da Esfera
pt.y = (screen.y – center.y)/radius; // radius : raio da esfera
r = pt.x*pt.x + pt.y*pt.y;
IF r > 1.0 THEN // Fora da Esfera
s = 1.0/sqrt[r];
pt.x = s*pt.x;
pt.y = s*pt.y;
pt.z = 0.0;
ElSE
pt.z = sqrt(1.0‐r)
ENDIF
ARCBALL
• Há duas possibilidades de algoritmos:
- Quaternions
- Eixo fixo de rotação e o ângulo que se deseja
rotacionar( Matriz de rotação).
ARCBALL
- Quaternions:
• Com os pontos, cria‐se dois quaternions p0 e p1
p0 = (x0,y0,z0,0) // x,y,z calculados no mapeamento
p1 = (x1,y1,z1,0) // x,y,z calculados no mapeamento
q = p1 p0*// onde p0* é o conjugado de p0
• q é o quaternion que descreve a rotação.
ARCBALL
-Ângulo e Eixo fixo de rotação:
Com os pontos, cria‐se dois vetores p0 e p1
p0 = (x0,y0,z0) // x,y,z calculados no mapeamento
p1 = (x1,y1,z1) // x,y,z calculados no mapeamento
vrot = p0 × p1 // Eixo de Rotação
ang = 2 * acos(p0 ∙ p1)// Angulo de Rotação
– Nesse caso gira‐se o ângulo correto, já em relação `a
quaternions o ângulo é a metade.
Referências
• [1] Notações de aula [ Marcelo Gattass]
• [2] ARCBALL:A User Interface for Specifying
• Three-Dimensional Orientation Using a
Mouse[Ken Shoemake]
• [3] Utilização de quatérnios para representação
de rotações em 3D[ Sergio Coutinho de Biasi e
Marcelo Gattass]