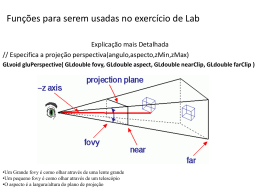
Projeções Clássicas
e
Matrizes de Projeção do OpenGL
Projeções Planas Cônicas
A
Ap
B
Bp
 realista
 não preserva escala
 não preserva ângulos
Projeções Planas Paralelas
A
Ap
B
Bp
 pouco realista
 preserva paralelismo
 possui escala conhecida
Classificação das projeções planas
 Paralelas
» ortográficas
– plantas
– elevações
– iso-métrica
» oblíquas
– cavaleiras
– cabinet
 Cônicas
» 1 pto de fuga
» 2 ptos de fuga
» 3 ptos de fuga
dp // n
dp não é paralela a n
Projeções de um cubo
• Paralelas
1
1
1
1/2
1
1
a
a
planta ou
elevação
iso-métrica
Cabinete
(a=45 ou 90)
Cavaleira
(a=45 ou 90)
• Cônicas
1 pto de fuga
2 ptos de fuga
Projeção plana é uma
transformação linear?
Ou seja:
T(P+Q) = T(P)+T(Q) e
T(aP) = aT(P) ?
2V
2V
V
(2V)p2(Vp)
Vp
plano de
projeção
2Vp
V
O
O
Vp
cp
cp
Projeções cônicas não são TL,
paralelas podem ser.
Projeção plana paralela é uma
transformação linear?
T(P+Q) = T(P)+T(Q) ?
P+Q
retas paralelas
projetam em paralelas
P
Pp
O
Pp+ Qp
Q
Pp
Qp
Qp
T( 0 ) = 0 ?
Projeção paralela em plano que passa
pela origem é uma transformação linear
Matrizes de projeções Cavaleiras
e Cabinetes
y
y
M
1
k
(1,1,1)
a
1
x
z
3
2
T(1,0,0) = (1,0)
T(0,1,0) = (0,1)
T(0,0,1) = ( -k cos a, -k sin a )
x
1
0
-k.cos(a)
0
1
-k.sin(a)
M =
Matrizes de projeções pseudoisométricas
y
y
M
j
1 jp
(1,1,1)
i
x
k
z
x
ip
kp
3
2
T(1,0,0) = (cos 30 ,-sin 30)
T(0,1,0) = (0,1)
T(0,0,1) = (-cos 30, -sin 30)
cos30
0
-cos30
-sin30
1
-sin30
M =
Projeção cônica simples
 xe 
 
P   ye 
z 
 e
ye
P
 xp 


Pp   y p 
 d 


Pp
ze
xe
zp = -d
xp
d
=
xe
-ze
xe
yp
xp
xp = d xe
-ze
yp
d
=
ye
-ze
ye
yp = d ye
-ze
-ze
d
d=n
ze
xe
ye
ze
Projeção cônica simples
xp = d xe
-ze
ye
P
yp = d ye
-ze
Pp
ze
xe
zp = -d
xp
d 0 0 0
xe
d xe
(d/-ze) xe
yp
0 d 0 0
ye
d ye
(d/-ze) ye
0 0 d 0
ze
0 0 -1 0
1
zp
1
=
=
d ze
=
-ze
w
-d
1
w
Simplificação da projeção cônica
Projeção cônica
Projeção ortográfica
eye
plano de projeção
direção de projeção
plano de projeção
Distorce o frustum de
visão para o espaço da tela
ze = -f
ye
ze
xe
ze = -n
[P]=
d=n
n
0
0
0
0
n
0
0
0
0
a

0
0
-1
0
ye
ze
xe
ze = -n
ze = -f
Uma equação para profundidade
ze  a 

n a 
Ptos no near (z=-n):
z
 f a 
Ptos no far (z=-f):
a  f  n

  f  n
[P]=
n
0
0
0
0
n
0
0
0
0
n+f
nf
0
0
-1
0

n

f
Translada o paralelepípedo de
visão para origem
t
ye
b
ze
xe
l
[T]=
r
1
0
0
-(r+l)/2
0
1
0
-(t+b)/2
0
0
1 +(f+n)/2
0
0
0
1
ye
(t-b)/2
-(t-b)/2
ze
-(r-l)/2
(r-l)/2
xe
(f-n)/2
-(f-n)/2
Escala o paralelepípedo de visão no cubo [-1,1]x[-1,1]x[-1,1]
ye
(t-b)/2
-(t-b)/2
ze
xe
-(r-l)/2
(r-l)/2
(f-n)/2
near
-(f-n)/2
far
2/(r-l)
0
0
0
0
2/(t-b)
0
0
0
0
0
0
[S] =
yd
1
1
1
zd
far
xd
-2/(f-n) 0
1
0
near
-1
-1
-1
Matriz Frustum do OpenGL
[P]=
[T]=
n
0
0
0
0
n
0
0
0
0 n+f n  f
0
0
-1
0
1
0
0
-(r+l)/2
0
1
0
-(t+b)/2
0
0
1 +(f+n)/2
0
0
0
[S T P ] =
1
 2n
r  l

 0

 0

 0

OpenGL Spec
[S] =
2/(r-l)
0
0
0
0
2/(t-b)
0
0
0
0
0
0
-2/(f-n) 0
0
1
0
2n
t b
0
0
r l
r l
t b
t b
 ( f  n)
f n
1

0 

0 

 2 fn 
f n
0 
Projeção Cônica (Frustum)
void glFrustum( GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top,
GLdouble near_, GLdouble far_ );
view frustum
ye
ze
xe
camera (eye)
Obs.: near e far são
distâncias( > 0)
top
xe
ye
bottom
right
left
Plano de projeção
far
near
ze
ze
Projeção Cônica (Perspective)
void glPerspective( GLdouble fovy, GLdouble aspect,
GLdouble near_, GLdouble far_ );
w
ye
ze
aspect = w/h
h
xe
near
far
fovy
ze
xe
Matriz Ortho do OpenGL
[T]=
[S] =
1
0
0
-(r+l)/2
0
1
0
-(t+b)/2
0
0
1 +(f+n)/2
0
0
0
1
OpenGL Spec
2/(r-l)
0
0
0
0
2/(t-b)
0
0
0
0
0
0
-2/(f-n) 0
0
1
Projeção Paralela
(Ortho)
near
top
ye
far
B  right top  far)
bottom
ze
xe
A
left
right
A  left bottom  near)
void glOrtho( GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top,
GLdouble near_, GLdouble far_ );
void gluOrtho2D( GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top );
Glu Look At
void gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez,
GLdouble centerx, GLdouble centery, GLdouble centerz,
GLdouble upx, GLdouble upy, GLdouble upz);
Dados:
eye, ref, up (definem o sistema de coordenadas do olho)
Determine a matriz que leva do sistema de Coordenadas dos Objetos
para o sistema de Coordenadas do Olho
up
eye
center
Coordenadas dos
Objetos
Coordenadas do
Olho
Calcula o sistema - xe ye ze
vup
eye
dados:
eye, center, up
view
y0
view = center - eye
center
vup
ze
x0
eye
z0
view
y0
center
x0
z0
ze = – view / ||view||
Calcula o sistema - xe ye ze
vup
ze
xe
eye
xe = (vup x ze) / ||vup x ze||
view
y0
center
ye
vup
x0
xe
ze
eye
z0
view
y0
ye
center
vup
ze
xe
x0
eye
view
z0
ye = ze x xe
Translada o eye para origem
ye
ze
xe
eye
1 0 0 -eyex
0 1 0 -eyey
[T]=
0 0 1 -eyez
000 1
y0
center
y0
ye
x0
z0
ze
xe
eye
z0
center
x0
Roda xe ye ze para xo yo zo
xex xey xez 0
y y y 0
[ R ] = ex ey ez
zex zey zez 0
0 0 0 1
y0
ye
ze
xe
eye
z0
center
ye , yo
x0
ze , zo
xe , xo
Matriz Look At do OpenGL
1 0 0 -eyex
0 1 0 -eyey
[T]=
0 0 1 -eyez
000 1
ze = – view / ||view||
xe = (vup x ze) / ||vup x ze||
ye = ze x xe
xex xey xez 0
y y y 0
[ R ] = ex ey ez
zex zey zez 0
0 0 0 1
[ R T ] =?
Concatenação das transformações
y0 ye
eye
[T]
[R]
ze
xe
z0
x0
ye
ze
xe
center
[P]
ye
ye
ze
xe
ze
eye
xe
[ T2 ]
ye
y0
ze
center
xe
[S]
x0
z0
ye
1
1
1
ze
far
xe
near
-1
-1
-1