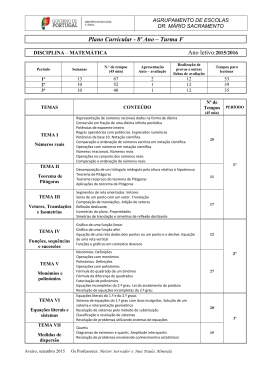
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Calendarização da Componente Letiva
2015/2016
7º Ano
Matemática
Períodos
1º
2º
3º
Período
Período
Período
Número de aulas previstas (45 minutos)
61
50
48
Apresentação e Diagnóstico
2
Avaliação (preparação, fichas de avaliação e correção)
7
7
7
Auto e Heteroavaliação
1
1
1
Lecionação de conteúdos
51
42
40
Total de aulas previstas: 159
Total de aulas para lecionação de conteúdos: 133
Temas / Conteúdos
Número de aulas previstas
por Período
1 - Números Racionais
 Adição e subtração com representação na reta numérica.
- Conjuntos numéricos;
- Representação de números racionais na reta numérica;
- Valor absoluto e simétrico;
- Adição e suas propriedades em
- Subtração em
;
;
- Simplificação da escrita;
1º Período
- Simétrico da soma e simétrico da diferença de dois
números racionais.
 Multiplicação e divisão em
- Multiplicação em
. Propriedades
;
- Propriedades da multiplicação em
- Divisão em
.
 Potências, raiz quadrada e raiz cúbica.
- Potências;
- Raiz quadrada;
;
51 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
- Raiz cúbica.

Atividades globais.
2. Funções
 Conceito de função e de gráfico de uma função.
- Referencial cartesiano;
- Correspondência entre conjuntos. Relações entre
variáveis;
- Variação de uma função;
- Expressões algébricas;
- Operar com funções.
 Função linear, função afim e função constante.
 Proporcionalidade direta como função.
 Atividades globais.
3. Sequências, sucessões e regularidades
 Termo geral de uma sequência numérica e de uma sucessão.
Representação
 Atividades globais.
4. Triângulos e quadriláteros
 Linhas poligonais e polígonos;
 Igualdade de triângulos;
 Propriedades, classificação e construção de quadriláteros:
- Classificação de quadriláteros;
- Propriedades de quadriláteros.
 Soma das amplitudes dos ângulos internos e externos de um
polígono de n lados;
 Áreas de quadriláteros.
 Atividades globais.
5. Equações
 Expressões algébricas;
 Noção de equação;
 Resolução de equações;
 Problemas;
2º Período
42 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
 Atividades globais.
6. Semelhanças
 Noção de semelhança;
 Segmentos de reta comensuráveis.
6. Semelhanças (continuação)
 Teorema de Tales.
 Semelhança de triângulos.
 Polígonos semelhantes:
- Relação
entre
perímetros
e
áreas
de
figuras
semelhantes;
 Homotetia de centro O e razão r.
 Atividades globais.
7. Tratamento de dados
 Organização, análise e interpretação de dados.
 Medidas de localização:
- Mediana.
 Atividades globais.
3º Período
40 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Calendarização da Componente Letiva
2015/2016
8º Ano
Turmas A, B, D, E e F
Matemática
Períodos
1º
2º
3º
Período
Período
Período
Número de aulas previstas (45 minutos)
61
50
48
Apresentação e Diagnóstico
2
Avaliação (preparação, fichas de avaliação e correção)
7
7
7
Auto e Heteroavaliação
1
1
1
Lecionação de conteúdos
51
42
40
Total de aulas previstas: 159
Total de aulas para lecionação de conteúdos: 133
Temas / Conteúdos
Número de aulas previstas
por Período
Semelhanças (7º ano)
 Segmentos de reta comensuráveis
 Polígonos semelhantes
- Relacionar perímetros e áreas de polígonos semelhantes;
- Relação entre os perímetros de dois círculos e as áreas de dois
quadrados.
 Homotetia de centro O e razão r.
1º Período
Teorema de Pitágoras
 Decomposição de um triângulo retângulo pela altura
referente à
hipotenusa
 Teorema de Pitágoras
- Demonstração;
- Determinar o comprimento da hipotenusa.
- Determinar o comprimento de um cateto;
- Recíproco do teorema de Pitágoras.
- Problemas envolvendo os teoremas de Pitágoras e de
51 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Tales e envolvendo a determinação de distâncias
desconhecidas por utilização destes teoremas.
Vetores, translações e isometrias

Segmentos orientados e vetores
Segmentos orientados;
 Segmentos orientados com a mesma direção e sentido e com a
mesma direção e sentidos opostos; comprimento de um
segmento orientado; segmento orientado reduzido a um ponto;
 Segmentos orientados equipolentes;
 Noção de vetor;
 Vetor nulo, vetores colineares e simétricos.
 Translação
 Noção de translação;
 Soma de um ponto com um vetor e translação determinada por
um vetor.
 Composição de translações e adição de vetores
 Composição de translações;
 Adição de vetores; regras do triângulo e do paralelogramo;
propriedades algébricas da adição algébrica de vetores;
 Propriedades das translações;
 Aplicação das propriedades.
 Reflexão deslizante. Propriedades das isometrias
 Reflexão deslizante;
 Reflexões deslizantes como isometrias;
 Propriedades das isometrias;
 Ação das isometrias sobre as retas, as semirretas e os ângulos e
respetivas amplitudes;
 Classificação das isometrias do plano;
 Translações como isometrias; caracterização pela preservação
da direção e sentido dos segmentos orientados e semirretas;
 Frisos e simetrias;
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)

Problemas envolvendo as propriedades das isometrias do
plano;
Problemas envolvendo figuras com simetrias de translação,
rotação, reflexão axial e reflexão deslizante.
 Números Racionais
 Representação de números racionais
 Conversão em fração de uma dízima infinita periódica;
 Caracterização das frações irredutíveis equivalentes a frações
decimais;
 Representação de números racionais através de dízimas finitas
ou infinitas periódicas utilizando o algoritmo da divisão; período
e comprimento do período de uma dízima;
 Representação na reta numérica de números racionais dados na
forma de dízima.
 Potências de expoente inteiro
 Potência de expoente nulo;
 Potência de expoente negativo;
 Extensão a potências de expoente inteiro das propriedades
conhecidas das potências de expoente natural;
 Decomposição decimal de uma dízima finita usando potências
de base 10 e expoente inteiro;
 Decomposição decimal de números racionais representados por
dízimas finitas, utilizando potências de base e expoente inteiro.
 Notação científica
 Representação de números em notação científica;
 Ordenação de números racionais representados na forma de
dízima ou em notação científica;
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
 Notação científica ( continuação)
 Operações com números escritos em notação científica.
Dízimas infinitas não periódicas e números reais
Conjunto dos números reais
 Dízimas infinitas não periódicas e «pontos irracionais».
Representação na reta numérica
 Definição de dízima infinita não periódica;
 Pontos irracionais da reta numérica;
 Conjunto dos números reais;
 Números irracionais;
 Números irracionais e dízimas infinitas não periódicas;
 Irracionalidade de
para
natural e distinto de um quadrado
perfeito;
 Construção da representação de raízes quadradas de números
naturais na reta numérica, utilizando o Teorema de Pitágoras.
2º Período
Operações com números reais
42 aulas
 Propriedades;
 Adição e subtração;
 Multiplicação e divisão;
 Potenciação;
 Método geométrico para determinar o produto de dois números
reais;
 Números reais; extensão a
das operações conhecidas sobre
e respetivas propriedades; extensão a medidas reais das
propriedades envolvendo proporções entre comprimentos de
segmentos.
 Relação de ordem em
 Comparar e ordenar números reais;
 Propriedades da relação de ordem em ;
 Extensão a
da ordem em
; propriedades transitiva e
tricotómica da relação de ordem; ordenação de números reais
representados na forma de dízima.
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Exercícios globais
Gráficos de funções afins
 Equação de uma reta não vertical e gráfico de função linear ou
afim
 Noção de função;
 Funções lineares e funções afins;
 Representação algébrica e gráfica de uma função afim;
 Identificar e representar o gráfico de uma função linear;
 Determinar a expressão algébrica de uma função linear;
 Equação de reta não vertical e gráfico de função linear ou afim;
 Relação entre os gráficos da função e da função definida por
.
 Declive e ordenada na origem de uma reta não vertical
 Parâmetro : declive da reta;
 Parâmetro : ordenada na origem;
 Declive e ordenada na origem de uma reta não vertical;
 Relação entre o declive e o paralelismo.
 Declive de uma reta determinada por dois pontos com
abcissas distintas. Equação de uma reta vertical
 Determinação do declive de uma reta;
 Equação de uma reta vertical.
Problemas envolvendo equações de retas.
Monómios, polinómios e equações do 2.º grau
 Monómios
 Monómios; fatores numéricos, constantes e variáveis ou
indeterminadas; parte numérica ou coeficiente; monómio nulo e
monómio constante; parte literal;
 Monómios semelhantes; forma canónica de um monómio;
igualdade de monómios;
 Grau de um monómio;
 Operações com monómios;
 Soma algébrica e produto de monómios.
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
 Polinómios
 Polinómios; termos; variáveis ou indeterminadas, coeficientes;
forma reduzida; igualdade de polinómios; termo independente;
polinómio nulo;
 Grau de um polinómio;
 Operações com polinómios;
 Soma algébrica e produto de polinómios.
 Casos notáveis da multiplicação de binómios
 Casos notáveis da multiplicação como igualdades entre
polinómios;
 Caso notável — Quadrado de um binómio;
Caso notável — Produto da soma de dois monómios pela sua
diferença;
Monómios, polinómios e equações do 2.º grau (Continuação)
 Fatorização de polinómios.

Problemas associando polinómios a medidas de áreas e
volumes, interpretando geometricamente igualdades que os
envolvam;

Problemas
envolvendo
polinómios,
casos
notáveis
da
multiplicação de polinómios e fatorização.
Equações do 2.º grau
 Equação do 2.º grau; equação incompleta;
 Lei do anulamento do produto;
 Resolução de equações do 2.º grau
 Resolução de equações de 2.º grau tirando partido da lei do
anulamento do produto.
Equações Literais e Sistemas
 Equações literais
 Resolução de equações literais;
 Resolução em ordem a uma dada incógnita de equações literais
3º Período
40 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
do 1.º e 2.º graus.
 Sistemas de duas equações do 1.º grau com duas incógnitas
 Definição e solução de um sistema;
 Sistemas de duas equações do 1.º grau com duas incógnitas;
forma canónica; soluções; sistemas equivalentes.
 Interpretação geométrica de sistemas de duas equações do
1.º grau com duas incógnitas
 Interpretação gráfica das soluções de um sistema;
 Sistema possível e determinado;
 Sistema impossível;
 Sistema possível e indeterminado.

Resolução de sistemas de equações
 Resolução de sistemas de duas equações de 1.º grau pelo
método de substituição;
 Resolução de problemas envolvendo sistemas de equações do
1.º grau com duas incógnitas.
Organização e tratamento de dados
 Organização, análise e interpretação de dados.
 Medidas de localização
 Noção de quartil;
 Extremos e quartis;
 Diagramas de extremos e quartis.
 Medidas de dispersão
 Amplitude;
 Amplitude interquartil.
Problemas envolvendo gráficos diversos e diagramas de extremos e
quartis.
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Calendarização da Componente Letiva
2015/2016
8º Ano Turmas C, G e H
Matemática
Períodos
1º
2º
3º
Período
Período
Período
Número de aulas previstas (45 minutos)
61
50
48
Apresentação e Diagnóstico
2
Avaliação (preparação, fichas de avaliação e correção)
7
7
7
Auto e Heteroavaliação
1
1
1
Lecionação de conteúdos
51
42
40
Total de aulas previstas: 159
Total de aulas para lecionação de conteúdos: 133
Temas / Conteúdos
Número de aulas previstas
por Período
Semelhanças (7º ano)
 Noção de semelhança
 Segmentos de reta comensuráveis
 Teorema de Tales.
 Semelhança de triângulos.
 Polígonos semelhantes
- Relacionar perímetros e áreas de polígonos semelhantes;
- Relação entre os perímetros de dois círculos e as áreas de dois
51 aulas
quadrados.
 Homotetia de centro O e razão r.
Teorema de Pitágoras
 Decomposição de um triângulo retângulo pela altura
referente à
1º Período
hipotenusa
 Teorema de Pitágoras
- Demonstração;
- Determinar o comprimento da hipotenusa.
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
- Determinar o comprimento de um cateto;
- Recíproco do teorema de Pitágoras.
- Problemas envolvendo os teoremas de Pitágoras e de
Tales e envolvendo a determinação de distâncias
desconhecidas por utilização destes teoremas.
Vetores, translações e isometrias

Segmentos orientados e vetores
Segmentos orientados;
 Segmentos orientados com a mesma direção e sentido e com a
mesma direção e sentidos opostos; comprimento de um
segmento orientado; segmento orientado reduzido a um ponto;
 Segmentos orientados equipolentes;
 Noção de vetor;
 Vetor nulo, vetores colineares e simétricos.
 Translação
 Noção de translação;
 Soma de um ponto com um vetor e translação determinada por
um vetor.
 Composição de translações e adição de vetores
 Composição de translações;
 Adição de vetores; regras do triângulo e do paralelogramo;
propriedades algébricas da adição algébrica de vetores;
 Propriedades das translações;
 Aplicação das propriedades.
 Reflexão deslizante. Propriedades das isometrias
 Reflexão deslizante;
 Reflexões deslizantes como isometrias;
 Propriedades das isometrias;
 Ação das isometrias sobre as retas, as semirretas e os ângulos e
respetivas amplitudes;
 Classificação das isometrias do plano;
 Translações como isometrias; caracterização pela preservação
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
da direção e sentido dos segmentos orientados e semirretas;
 Frisos e simetrias;
 Problemas envolvendo as propriedades das isometrias do plano;
Problemas envolvendo figuras com simetrias de translação,
rotação, reflexão axial e reflexão deslizante.
 Números Racionais
 Representação de números racionais
 Conversão em fração de uma dízima infinita periódica;
 Caracterização das frações irredutíveis equivalentes a frações
decimais;
 Representação de números racionais através de dízimas finitas
ou infinitas periódicas utilizando o algoritmo da divisão; período
e comprimento do período de uma dízima;
 Representação na reta numérica de números racionais dados na
forma de dízima.
 Potências de expoente inteiro
 Potência de expoente nulo;
 Potência de expoente negativo;
 Extensão a potências de expoente inteiro das propriedades
conhecidas das potências de expoente natural;
 Potências de expoente inteiro (continuação)
 Decomposição decimal de uma dízima finita usando potências
de base 10 e expoente inteiro;
 Decomposição decimal de números racionais representados por
dízimas finitas, utilizando potências de base e expoente inteiro.
 Notação científica
 Representação de números em notação científica;
 Ordenação de números racionais representados na forma de
dízima ou em notação científica;
 Operações com números escritos em notação científica.
2º Período
42 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Dízimas infinitas não periódicas e números reais
Conjunto dos números reais
 Dízimas infinitas não periódicas e «pontos irracionais».
Representação na reta numérica
 Definição de dízima infinita não periódica;
 Pontos irracionais da reta numérica;
 Conjunto dos números reais;
 Números irracionais;
 Números irracionais e dízimas infinitas não periódicas;
 Irracionalidade de
para
natural e distinto de um quadrado
perfeito;
 Construção da representação de raízes quadradas de números
naturais na reta numérica, utilizando o Teorema de Pitágoras.
Operações com números reais
 Propriedades;
 Adição e subtração;
 Multiplicação e divisão;
 Potenciação;
 Método geométrico para determinar o produto de dois números
reais;
 Números reais; extensão a
das operações conhecidas sobre
e respetivas propriedades; extensão a medidas reais das
propriedades envolvendo proporções entre comprimentos de
segmentos.
 Relação de ordem em
 Comparar e ordenar números reais;
 Propriedades da relação de ordem em ;
 Extensão a
da ordem em
; propriedades transitiva e
tricotómica da relação de ordem; ordenação de números reais
representados na forma de dízima.
Exercícios globais
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Gráficos de funções afins
 Equação de uma reta não vertical e gráfico de função linear ou
afim
 Noção de função;
 Funções lineares e funções afins;
 Representação algébrica e gráfica de uma função afim;
 Identificar e representar o gráfico de uma função linear;
 Determinar a expressão algébrica de uma função linear;
 Equação de reta não vertical e gráfico de função linear ou afim;
 Relação entre os gráficos da função e da função definida por
.
 Declive e ordenada na origem de uma reta não vertical
 Parâmetro : declive da reta;
 Parâmetro : ordenada na origem;
 Declive e ordenada na origem de uma reta não vertical;
 Relação entre o declive e o paralelismo.
 Declive de uma reta determinada por dois pontos com
abcissas distintas. Equação de uma reta vertical
 Determinação do declive de uma reta;
 Equação de uma reta vertical.
Problemas envolvendo equações de retas.
Monómios, polinómios e equações do 2.º grau
 Monómios
 Monómios; fatores numéricos, constantes e variáveis ou
indeterminadas; parte numérica ou coeficiente; monómio nulo e
monómio constante; parte literal;
 Monómios semelhantes; forma canónica de um monómio;
igualdade de monómios;
 Grau de um monómio;
 Operações com monómios;
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
 Soma algébrica e produto de monómios.
 Polinómios
 Polinómios; termos; variáveis ou indeterminadas, coeficientes;
forma reduzida; igualdade de polinómios; termo independente;
polinómio nulo;
 Grau de um polinómio;
 Operações com polinómios;
 Soma algébrica e produto de polinómios.
Monómios, polinómios e equações do 2.º grau (Continuação)
 Casos notáveis da multiplicação de binómios
 Casos notáveis da multiplicação como igualdades entre
polinómios;
 Caso notável — Quadrado de um binómio;
Caso notável — Produto da soma de dois monómios pela sua
diferença;
 Fatorização de polinómios.
Problemas associando polinómios a medidas de áreas e volumes,
interpretando geometricamente igualdades que os envolvam;
Problemas envolvendo polinómios, casos notáveis da multiplicação
de polinómios e fatorização.
Equações do 2.º grau
 Equação do 2.º grau; equação incompleta;
 Lei do anulamento do produto;
 Resolução de equações do 2.º grau
 Resolução de equações de 2.º grau tirando partido da lei do
anulamento do produto.
Equações Literais e Sistemas
 Equações literais
 Resolução de equações literais;
 Resolução em ordem a uma dada incógnita de equações literais
3º Período
40 aulas
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
do 1.º e 2.º graus.
 Sistemas de duas equações do 1.º grau com duas incógnitas
 Definição e solução de um sistema;
 Sistemas de duas equações do 1.º grau com duas incógnitas;
forma canónica; soluções; sistemas equivalentes.
 Interpretação geométrica de sistemas de duas equações do
1.º grau com duas incógnitas
 Interpretação gráfica das soluções de um sistema;
 Sistema possível e determinado;
 Sistema impossível;
 Sistema possível e indeterminado.

Resolução de sistemas de equações
 Resolução de sistemas de duas equações de 1.º grau pelo
método de substituição;
 Resolução de problemas envolvendo sistemas de equações do
1.º grau com duas incógnitas.
Organização e tratamento de dados
 Organização, análise e interpretação de dados.
 Medidas de localização
 Noção de quartil;
 Extremos e quartis;
 Diagramas de extremos e quartis.
 Medidas de dispersão
 Amplitude;
 Amplitude interquartil.
Problemas envolvendo gráficos diversos e diagramas de extremos e
quartis.
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Calendarização da Componente Letiva
2015/2016
9º Ano Turmas A e B
Matemática
Períodos
1º
2º
3º
Período Período
Número de aulas previstas (45 minutos)
61
Apresentação e Diagnóstico
2
Avaliação (preparação, fichas de avaliação e correção)
Período
50
43
7
7
7
Auto e Heteroavaliação
1
1
1
Lecionação de conteúdos
51
42
35
Total de aulas previstas: 154
Total de aulas para lecionação de conteúdos: 128
Temas / Conteúdos
Número de aulas
previstas por Período
0. Resolução de sistemas de equações

Resolução de sistemas de duas equações de 1.º grau pelo
método de substituição;

Resolução de problemas envolvendo sistemas de equações
do 1.º grau com duas incógnitas.

Atividades globais
1. Estatística e probabilidades



Organização, análise e interpretação de dados.
Medidas de localização
o
Mediana
o
Noção de quartil
o
Extremos e quartis
o
Diagramas de extremos e quartis
Medidas de dispersão
o
Amplitude
1º Período
51
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
o

Amplitude interquartil
Problemas envolvendo gráficos diversos e diagramas de
extremos e quartis
1.1.
Organizar e representar dados em histogramas
1.2.
Experiência e conjunto de resultados
1.3.
Acontecimentos elementares, compostos, certos e
impossíveis
1.4.
Acontecimentos incompatíveis e complementares
1.5.
Probabilidade de um acontecimento
- Escala de probabilidades
1.6.
Conceito frequencista de probabilidade
1.7.
Conceito clássico de probabilidade: Lei de Laplace
1.8.
Processos organizados de contagem
 Atividades globais
2. Funções
 Rever e aplicar
2.1.
Proporcionalidade inversa
2.2.
Função de proporcionalidade inversa
2.3.
Representação gráfica (de funções de proporcionalidade
inversa)
2.4.
Resolução de problemas
2.5.
Função quadrática
 Atividades globais
3. Equações

Rever e aplicar
3.1. Completar e quadrado
3.2. Equações do 2º grau completas
3.3. Fórmula resolvente
3.4. Binómio discriminante
3.5. A função quadrática e as equações do 2º grau
3.6. Problemas envolvendo equações do 2º grau

Atividades globais
2º Período
42
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
4. Geometria

Rever e aplicar
4.1. Algumas noções de Lógica Matemática
4.2. Método axiomático
4.3. Axioma euclidiano de paralelismo
4.4. Pontos, retas e planos
4.5. Sólidos

Atividades globais
4.6. Lugares geométricos
4.7. Circuncentro de um triângulo
4.8. Incentro de um triângulo
4.9. Ortocentro de um triângulo
4.10. Baricentro de um triângulo
4.11. Arcos e cordas de uma circunferência
4.12. Medida da amplitude de um ângulo ao centro
4.13. Propriedades geométricas em circunferências
4.14. Comprimento de um arco de circunferência e área de um
sector circular
4. Geometria (continuação)
4.15. Ângulos
4.16. Ângulos internos e externos de um polígono
4.17. Polígonos inscritos numa circunferência

Atividades globais
5. Números reais e inequações

Rever e aplicar
5.1. Relação de ordem em IR. Propriedades
5.2. Intervalos de números reais
5.3. Interseção e reunião de intervalos
5.4. Valores aproximados
5.5. Inequações
5.6. Inequações do 1º grau
3º Período
35
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
5.7. Disjunção de inequações
5.8. Conjunção de inequações

Atividades globais
6. Trigonometria no triângulo retângulo

Rever e aplicar
6.1. Razões trigonométricas de ângulos agudos.
6.2. Relações entre as razões trigonométricas
6.3. Tabelas e calculadora.
6.4. Valores exatos das razões trigonométricas dos ângulos de
amplitude 45º, 60º e 30º
6.5. A trigonometria na resolução de problemas

Atividades globais
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
Calendarização da Componente Letiva
2015/2016
9º Ano Turmas C, D, E, F e G
Matemática
Períodos
1º
2º
3º
Período
Período
Período
Número de aulas previstas (45 minutos)
61
50
43
Apresentação e Diagnóstico
2
Avaliação (preparação, fichas de avaliação e correção)
7
7
7
Auto e Heteroavaliação
1
1
1
Lecionação de conteúdos
51
42
35
Total de aulas previstas: 154
Total de aulas para lecionação de conteúdos: 128
Temas / Conteúdos
Número de aulas previstas
por Período
Estatística e probabilidades

Medidas de localização
- Noção de quartil
- Extremos e quartis
- Diagramas de extremos e quartis

Medidas de dispersão
- Amplitude
- Amplitude interquartil

1º Período
Atividades globais
51
1.1. Organizar e representar dados em histogramas
1.2. Experiência e conjunto de resultados
1.3. Acontecimentos
elementares,
compostos,
certos
impossíveis
1.4. Acontecimentos incompatíveis e complementares
1.5. Probabilidade de um acontecimento
- Escala de probabilidades
1.6. Conceito frequencista de probabilidade
1.7. Conceito clássico de probabilidade: Lei de Laplace
e
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
1.8. Processos organizados de contagem

Atividades globais
Funções

Rever e aplicar
2.1. Proporcionalidade inversa
2.2. Função de proporcionalidade inversa
2.3. Representação gráfica (de funções de proporcionalidade
inversa)
2.4. Resolução de problemas
2.5. Função quadrática

Atividades globais
Equações

Rever e aplicar
3.1. Completar e quadrado
3.2. Equações do 2º grau completas
3.3. Fórmula resolvente
3.4. Binómio discriminante
3.5. A função quadrática e as equações do 2º grau
Equações (continuação)
3.6.

Problemas envolvendo equações do 2º grau
Atividades globais
Geometria

Rever e aplicar
6.1. Algumas noções de Lógica Matemática
6.2. Método axiomático
6.3. Axioma euclidiano de paralelismo
6.4. Pontos, retas e planos
6.5. Sólidos

Atividades globais
6.6. Lugares geométricos
6.7. Circuncentro de um triângulo
6.8. Incentro de um triângulo
6.9. Ortocentro de um triângulo
2º Período
42
AGRUPAMENTO DE ESCOLAS
ANDRÉ SOARES (150952)
6.10. Baricentro de um triângulo
6.11. Arcos e cordas de uma circunferência
6.12. Medida da amplitude de um ângulo ao centro
6.13. Propriedades geométricas em circunferências
6.14. Comprimento de um arco de circunferência e área de um
sector circular
6.15. Ângulos
Geometria (continuação)
5.15. Ângulos
5.16. Ângulos internos e externos de um polígono
5.17. Polígonos inscritos numa circunferência

Atividades globais
Números reais e inequações

Rever e aplicar
8.1. Relação de ordem em
. Propriedades
8.2. Intervalos de números reais
8.3. Interseção e reunião de intervalos
8.4. Valores aproximados
8.5. Inequações
8.6. Inequações do 1º grau
8.7. Disjunção de inequações
8.8. Conjunção de inequações

Atividades globais
Trigonometria no triângulo retângulo

8.1.
Rever e aplicar
Razões trigonométricas de ângulos agudos.
8.2. Relações entre as razões trigonométricas
8.3. Tabelas e calculadora.
8.4. Valores exatos das razões trigonométricas dos ângulos de
amplitude 45º, 60º e 30º
8.5. A trigonometria na resolução de problemas

Atividades globais
3º Período
35