Capı́tulo 18
Problemas de Máximo e Mı́nimos em
Intervalos quaisquer
18.1
Introdução
No Cap. 15 estudamos o problema de determinar máximos e mı́nimos globais para funções contı́nuas definidas em
intervalos fechados. Visto que o teorema dos valores extremos para funções contı́nuas garante, para estas funções, a existência de extremos globais, e como tais extremos só podem ocorrer nos pontos crı́ticos da função ou nas extremidades
do intervalo onde esta função está definida, o critério empregado foi o de comparar os valores da função f calculados
nos extremos do intervalo com os valores de f nos seus pontos crı́ticos. No entanto, em vários problemas a função f
que descreve a grandeza a ser maximizada é definida em um intervalo aberto (a, b) e até mesmo em um intervalo não
limitado, por exemplo, (0, ∞). Neste caso, não podemos empregar a técnica descrita acima. Não podemos nem sequer
garantir, a priori, a existência de máximos e mı́nimos globais. O teste da derivada segunda é útil nestes casos.
Suponhamos que queiramos maximizar, ou minimizar, uma função derivável f num intervalo aberto I, e constatemos que f tem apenas um ponto crı́tico em I, isto é, um número c para o qual f ′ (c) = 0. Se f ′′ (x) tiver o mesmo
sinal em todos os pontos de I, o teste da derivada segunda nos diz que o ponto c é um extremo absoluto de f em I.
Este extremo será um mı́nimo se f ′′ (c) > 0 e, um máximo se f ′′ (c) < 0.
Os exemplos a seguir ilustram o uso deste teste.
18.2
Exemplos
Exemplo 1
Um fabricante de latas cilı́ndricas de conservas recebe um pedido muito grande de latas com determinado volume
V0 . Quais as dimensões que minimizarão a área lateral da superfı́cie de uma lata como esta e, portanto, a quantidade
de metal necessário para fabricá-la?
Solução
Sendo r e h, respectivamente, o raio da base e a altura de uma lata cilı́ndrica, seu volume será dado por
(1)
V0 = π r 2 h
e a área lateral por
(2)
A = 2 π r2 + 2 π r h.
Queremos minimizar A, que é uma função de duas variáveis relacionadas pela equação (1). Resolvendo (1) para h
e substituindo em (2),
>
h:=solve(V[0]=Pi*r^2*h,h);
V0
h=
π r2
>
subs(h=V[0]/(Pi*r^2),A=2*Pi*r^2+2*Pi*r*h);
V0
A = 2 π r2 + 2
,
r
onde r pertence ao intervalo (0, ∞). Como sabemos, os extremos desta função, caso existam, estarão localizados em
um de seus pontos crı́ticos. Assim, derivamos a equação acima e resolvemos a equação resultante ao igualarmos esta
derivada a zero:
>
diff(2*Pi*r^2+2*V[0]/r,r);
242
Cap. 18. Problemas de Máximo e Mı́nimos em Intervalos quaisquer
V0
r2
2 V0
V0 13
Mas, 4 π r − r2 = 0 se r = ( 2 π ) . A derivada segunda desta função é dada por
>
diff(2*Pi*r^2+2*V[0]/r,r,r);
V0
A′′ = 4 π + 4 3
r
que é sempre positiva, pois r é positivo.
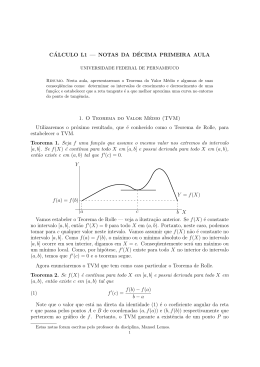
Assim, a função A(r) é côncava para cima em todo o seu domı́nio e o ponto crı́tico 4 π +
para esta função. Veja o gráfico de A para V0 = 500 ml
A′ := 4 π r − 2
4 V0
r3
é um mı́nimo absoluto
1000
800
600
y
400
200
0
2
4
6
8
10
r
12
14
16
18
20
As dimensões da lata de custo mı́nimo podem ser obtidas, a partir da equação (1), calculando-se o valor de h,
correspondente ao valor de r, onde a função A atinge o seu mı́nimo. Assim,
h=
V0
V0 1
= 2(
)3 .
π r2
2π
Note que h = 2 r.
Do ponto de vista de diminuir custos de matéria-prima, esse resultado revela que a “melhor” proporção para uma
lata cilı́ndrica é aquela em que a altura é igual ao diâmetro da base. Esta é a proporção usada em latas de leite em pó,
salsichas, extrato de tomate, etc. Você é capaz de explicar por que esta não é a proporção empregada na fabricação
de latas de óleo de cozinha?
Exemplo 2
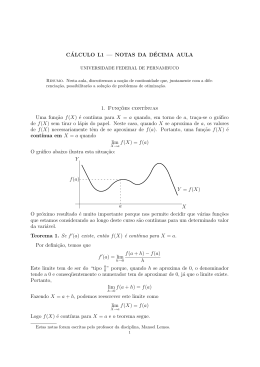
Determine a razão entre a altura e o diâmetro da base do cilindro de volume máximo que pode ser inscrito numa
esfera de raio R.
Solução As figuras mostram um cilindro inscrito numa esfera juntamente com um corte transversal do mesmo:
y
R
x
O volume do cilindro será dado, então, por V = 2 π x2 y. Além disso, pelo teorema de Pitágoras podemos concluir
que as variáveis x e y estão relacionadas pela equação x2 + y 2 = R2 .
Podemos perceber, também, que V é pequeno quando x está perto de zero ou quando x está perto de R, portanto,
entre estes extremos existe uma posição de volume máximo. Para achá-la, substituı́mos o valor de x2 na equação que
define V e obtemos a equação V = 2 π y (R2 − y 2 ). Derivando esta equação em relação a y, temos
>
diff(2*Pi*y*(R^2-y^2),y);
V ′ = 2 π (R2 − y 2 ) − 4 π y 2
>
simplify(%);
′
V ′ = 2 π R2 − 6 π y 2
Resolvendo a equação V (y) = 0, obtemos
>
solve({diff(2*Pi*y*(R^2-y^2),y)=0},{y});
W.Bianchini, A.R.Santos
243
1√
1√
3 R}, {y = −
3 R}
3
3
√
Aplicando o teste da derivada segunda, comprovamos que o ponto y = 33 R é realmente um ponto de máximo para
a função, pois
>
derivada_segunda=diff(2*Pi*y*(R^2-y^2),y,y);
{y =
derivada segunda = −12 π y
e esta derivada é negativa para
valores positivos de y. Substituindo o valor positivo encontrado para y na igualdade
√
x2 + y 2 = R2 , obtemos x = √23R . Concluı́mos, então que a razão entre a altura e o diâmetro da base do cilindro de
maior volume inscrito numa esfera de raio R é
√
y
2
=
x
2
Exemplo 3
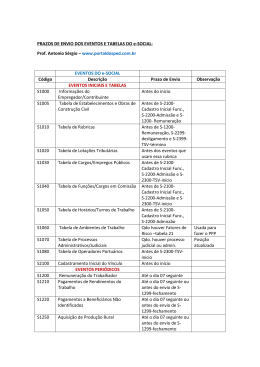
Determinar o comprimento da maior vara que pode ser transportada horizontalmente, através da quina de um
corredor de 2 m de largura para outro de 4 m de largura, conforme é esquematizado no desenho a seguir.
Solução:
Conforme mostra a figura, o comprimento desejado é o comprimento mı́nimo L = L1 + L2 da vara. Pelos dois triângulos semelhantes da figura, vemos que
L2
4
= sen(θ)
L1
e
θ
2
= cos(θ)
L2
L1
de modo que
θ
L1 = 4 csc(θ)
e
L2 = 2 sec(θ) .
Portanto, o comprimento L = L1 + L2 da vara é uma função de θ, dada por
L(θ) = 4 csc(θ) + 2 sec(θ) ,
onde θ varia no intervalo aberto (0, π2 ). Note que L → ∞ quando θ → 0 pela direita ou quando θ →
(Por quê?) Calculando a derivada de L(θ) e igualando a expressão resultante a zero, temos
>
diff(4*csc(theta)+2*sec(theta),theta);
−4 csc(θ) cot(θ) + 2 sec(θ) tan(θ)
>
solve(-4*csc(theta)*cot(theta)+2*sec(theta)*tan(theta)=0,theta);
1
1 √
1
1 √
arctan(21/3 ), arctan(− 21/3 + I 3 21/3 ), arctan(− 21/3 − I 3 21/3 )
2
2
2
2
π
2
pela esquerda.
1
Logo, θ = arctg(2 3 ) é a raiz que nos interessa. Este valor é aproximadamente igual a
>
evalf(arctan(2^(1/3)));
.8999083481
Vamos agora calcular a derivada segunda da função L, para comprovar que o ponto que achamos é, de fato, o mı́nimo
da função L.
>
derivada_segunda:=diff(4*csc(theta)+2*sec(theta),theta,theta);
derivada segunda :=
4 csc(θ) cot(θ)2 − 4 csc(θ) (−1 − cot(θ)2 ) + 2 sec(θ) tan(θ)2 + 2 sec(θ) (1 + tan(θ)2 )
>
evalf(subs(theta=0.9,derivada_segunda));
24.97376536
Como a derivada segunda no ponto crı́tico é positiva e este é o único ponto crı́tico da função (as demais raı́zes da
equação L′ (θ) = 0 são complexas), vemos que o mı́nimo absoluto de L e, portanto, o comprimento máximo da vara, é
cerca de
>
evalf(4*csc(0.9)+2*sec(0.9));
8.323876472
244
Cap. 18. Problemas de Máximo e Mı́nimos em Intervalos quaisquer
ou seja, aproximadamente 8,32 metros.
Exemplo 4: Reflexão da luz
Um raio de luz parte de um ponto A, atinge um ponto P sobre
um espelho plano, sendo então refletido e passando por um ponto
B, como mostra a figura abaixo. Medidas acuradas mostram que
o raio incidente e o raio refletido formam ângulos iguais com o
espelho, isto é α = β. Suponha que o raio de luz siga o caminho
mais curto de A a B, passando pelo ponto P no espelho. Prove
a lei de reflexão, mostrando que o caminho APB é mais curto
quando α = β.
B
A
b
a
α
x
β
c-x
P
c
Solução Repare que o ponto P pode assumir várias posições no espelho e cada uma destas posições é determinada
por um valor de x. Vamos considerar, portanto, o comprimento L do caminho percorrido pelo raio de luz como uma
função de x. A partir da figura, podemos concluir que
√
√
L = a2 + x2 + b2 + (c − x)2 .
Derivando esta função, temos
>
L:=x->sqrt(a^2+x^2)+sqrt(b^2+(c-x)^2):
>
diff(L(x),x);
L′ (x) = √
x
1
−2 c + 2 x
+ √
2
2
2 b + c2 − 2 c x + x2
+x
a2
Minimizamos L ao igualar esta derivada a zero, obtendo:
√
x
c−x
=√
a2 + x2
b2 + c2 − 2 c x + x2
e daı́, podemos concluir que cos(α) = cos(β). Como α e β estão no primeiro quadrante, segue que α = β.
Para verificar que realmente minimizamos L, basta calcular a derivada segunda de L e observar que esta derivada
é sempre positiva para qualquer valor de x. De fato,
d2 L
a2
b2
=
+
.
3
3
dx 2
(a2 + x2 )( 2 )
(b2 + (c − x)2 )( 2 )
Exemplo 5: Refração da luz
O raio de luz refletido que acabamos de discutir no exemplo anterior mantém a velocidade constante quando
atravessa um único meio. No entanto, em meios diferentes (ar, água, vidro) a luz tem velocidades diferentes. Se um
raio de luz passa do ar para a água, é refratado passando a ter uma direção mais próxima da perpendicular à interface.
Veja a figura:
Ar
A
a
α
va
α
x
P
′
Agua
c-x
β
vw
b
β
B
c
O percurso APB, nitidamente, não é mais o caminho mais curto de A até B. Em 1621, o cientista holandês Snell
descobriu, empiricamente, que o caminho real do raio de luz é o que satisfaz a relação sen(α)
sen(β) = constante, onde esta
constante é independente das posições de A e de B. Esse fato é chamado lei de refração de Snell.
Prove a lei de Snell, partindo do pressuposto de que o raio percorre um caminho de A a B de modo a minimizar o
tempo total de percurso.
W.Bianchini, A.R.Santos
245
Solução Se a velocidade da luz no ar é va e na água é vw , então o tempo total de percurso T é a soma do tempo
que a luz gasta atravessando o ar com o tempo gasto para atravessar a água e é dado por
√
√
b2 + (c − x)2
a2 + x2
T =
+
.
va
vw
Calculando a derivada dessa função e observando o seu significado geométrico em termos da figura, obtemos:
>
>
T:=x->sqrt(a^2+x^2)/v[a]+sqrt(b^2+(c-x)^2)/v[w];
√
√
b2 + (c − x)2
a2 + x2
T := x →
+
va
vw
diff(T(x),x)=sen(alpha)/v[a]-sen(beta)/v[w];
T ′ (x) = √
a2
x
1
−2 c + 2 x
sen(α) sen(β)
+ √
=
−
2
2
2
2
2
va
vw
+ x va
b + c − 2 c x + x vw
Para conseguir o tempo mı́nimo de percurso, igualamos essa derivada a zero, obtendo
sen(α)
sen(β)
=
va
vw
ou
sen(α)
va
=
= constante
sen(β)
vw
Esta é a forma mais reveladora da lei de Snell, porque nos dá o significado fı́sico da constante que aparece na
equação. Esta constante é a razão entre a velocidade da luz no ar e a velocidade (menor) da luz na água. Essa
constante chama-se ı́ndice de refração da água. Se, nesse exemplo, a água for substituı́da por qualquer outro meio
translúcido, tal com álcool, glicerina ou vidro, então a constante terá um valor numérico diferente que será dado pelo
ı́ndice de refração do meio em questão.
Como no exemplo anterior, podemos verificar que a resposta obtida realmente minimiza T , calculando a segunda
derivada e observando que esta é positiva. De fato,
d2 T
a2
b2
=
+
> 0.
3
3
dx 2
va (a2 + x2 )( 2 )
vw (b2 + (c − x)2 )( 2 )
18.3
Problemas propostos
1. Determine a constante a de modo que a função f (x) = x2 + xa , para x ̸= 0, tenha um mı́nimo relativo em x = 2.
2. Uma grande vara deve passar por um canto retangular de um corredor, seguindo de uma parte de largura a para
outra de largura b. Se o comprimento da vara é L, qual a largura mı́nima b para que a manobra seja possı́vel?
3. Uma caixa retangular com base quadrada deve ser feita de madeira compensada. Sendo dado o seu volume, ache
a forma (razão entre a altura e o lado da base) que minimiza a quantidade de madeira compensada necessária.
Resolva este problema supondo, agora, que a caixa é aberta em cima.
4. Ache o raio do cilindro de volume máximo que pode ser inscrito num cone de altura H e raio da base R.
5. Ache a altura do cone de máximo volume que pode ser inscrito numa esfera de raio R.
6. Um tanque cilı́ndrico sem tampa deve ter um volume especificado. Se o custo do material usado para a base é
três vezes maior que o custo daquele usado para a lateral encurvada, ache a razão entre a altura e o diâmetro
da base para a qual o custo total é mı́nimo.
√
3
7. (a) Calcule as coordenadas do ponto do gráfico da função y = x mais próximo
√ do ponto ( 2 , 0).
Sugestão: Minimize o quadrado da distância do ponto dado ao ponto (x, x).
√
(b) Generalize o item anterior: ache o ponto sobre o gráfico de y = x que está mais próximo do ponto (a, 0)
para a > 0, qualquer.
(c) Determine o ponto da parábola y = x2 mais próximo do ponto (6, 3).
246
Cap. 18. Problemas de Máximo e Mı́nimos em Intervalos quaisquer
8. (a) Suponha que f seja uma função derivável definida em toda a reta, e que o gráfico de f contenha um ponto
0
Q(x, y) que está mais perto do ponto P (x0 , y0 ) que não está no gráfico. Mostre que f ′ (x) = − x−x
y−y0 , em Q.
Conclua que o segmento P Q é perpendicular à reta tangente à curva em Q.
(b) Use o resultado acima para mostrar que a distância mı́nima do ponto (x0 , y0 ) a um ponto da reta
+B y0 +C|
A x + B y + C = 0 é |A x√0A
.
2 +B 2
9. Duas discotecas, uma delas quatro vezes mais barulhenta do que a outra, estão situadas em extremidades opostas
de um quarteirão de 1000 m de comprimento. Qual é o ponto menos barulhento entre as discotecas? A intensidade
do ruı́do em um ponto distante da fonte é diretamente proporcional ao ruı́do e inversamente proporcional ao
quadrado da distância à fonte.
10. (a) Um triângulo isósceles está circunscrito a um cı́rculo de raio R. Se x é a altura do triângulo, mostre que
sua área é mı́nima quando x = 3R.
Sugestão: Minimize A2 .
(b) Se a figura descrita em (a) for girada ao redor da altura do triângulo, o resultado é um cone inscrito numa
esfera de raio R. Mostre que o volume do cone é mı́nimo quando x = 4 R e que esse volume é o dobro do
volume da esfera.
11. (a) Um silo tem parede cilı́ndrica, piso plano circular e teto hemisférico. Para um dado volume, ache a razão
entre a altura total e o diâmetro da base que minimiza a área da superfı́cie total.
(b) No item anterior, se o custo de construção por metro quadrado do teto hemisférico é o dobro do custo da
parede e do piso, ache a razão entre a altura total e o diâmetro da base que minimiza o custo total de
construção.
√
12. Qual o menor valor da constante a para o qual a desigualdade 2 2 ≤ a x +
positivos x ?
1
x
seja válida para todos os números
13. Um espião é deixado por um submarino para ser embarcado em um bote a 2 km de um ponto P numa praia reta
com direção norte-sul. Ele precisa chegar a uma casa na praia a 6 km ao norte de P. Remando, ele percorre 3
km/h e, andando, 5 km/h. Sua intenção é remar em direção a um certo ponto ao norte de P e depois andar o
resto do caminho.
(a) A que distância ao norte de P ele deve desembarcar para chegar à casa no menor tempo possı́vel?
(b) Qual a duração da viagem?
(c) Quanto tempo a mais ele gastará se remar diretamente a P e depois andar até a casa?
(d) Mostre que a resposta do item (a) deste problema não se altera se a casa estiver a 8 km ao norte de P.
(e) Se o bote do espião estiver munido de um pequeno motor que desenvolve uma velocidade de 5 km/h, então,
utilizando apenas o nosso bom senso, é óbvio que a rota mais rápida será a que for percorrida exclusivamente
de bote. Qual a menor velocidade em que tal rota continua sendo a mais rápida?
18.4
Um pouco de história: Princı́pio do tempo mı́nimo de Fermat
As idéias do Exemplo 5 foram descobertas em 1657 pelo grande matemático francês Pierre Fermat, e por essa razão
a afirmação de que um raio de luz atravessa um sistema ótico percorrendo o caminho que minimiza o tempo total de
percurso chama-se princı́pio do tempo mı́nimo de Fermat. É importante ressaltar que quando um raio de luz percorre
um único meio uniforme, “caminho mais curto” é equivalente a “tempo mı́nimo”, e assim o Exemplo 4 recai também
neste mesmo princı́pio.
Durante os dois séculos seguintes, as idéias de Fermat estimularam um amplo desenvolvimento da teoria geral de
máximos e mı́nimos, levando primeiro à criação por Euler (1701-1783) do Cálculo Variacional – um ramo da matemática
que procura achar os extremos de funções em um contexto mais geral do que aquele estudado no Cálculo Diferencial
– e depois, ao princı́pio da mı́nima ação, de Hamilton (1805-1865), que se tornou um dos princı́pios unificadores mais
profundos da Fı́sica. Euler expressou seu entusiasmo com as seguintes palavras memoráveis: “Como a estrutura do
mundo é a mais perfeita e foi estabelecida pelo mais sábio Criador, tudo que ocorre nesse mundo obedece a algum
princı́pio de máximo ou mı́nimo”.
W.Bianchini, A.R.Santos
18.5
247
Para você meditar: Como os gregos eram espertos ou uma demonstração sem palavras
A lei de reflexão discutida no Exemplo 4 já era conhecida pelos gregos da Antiguidade. No entanto, o fato de que um
raio de luz refletido segue o caminho mais curto foi descoberto muito mais tarde por Heron de Alexandria, no século
I D.C. A demonstração geométrica de Heron é simples, porém engenhosa. O desenho a seguir ilustra o argumento
empregado por ele.
• Demonstre a lei da reflexão usando a figura abaixo para justificar seu raciocı́nio. Nesta figura B ′ é a imagem
especular de B.
B
A
α
P’
β
γ
P
B’
18.6
Projetos
18.6.1
Um problema de otimização
Otimizar é uma das mais importantes aplicações de derivada. Os problemas aplicados que usualmente são estudados
num curso de Cálculo são, necessariamente, muito simples para que a aplicação dos conceitos matemáticos não sejam
sobrepujadas por cálculos longos e cansativos. O objetivo deste projeto é apresentar um problema um pouco mais
real. Nele, você é o gerente de planejamento de uma companhia elétrica e a você é designada a seguinte tarefa:
A Companhia deve estender um cabo de alta tensão partindo de uma usina localizada dentro de uma reserva florestal
até uma fábrica em construção. A fábrica está a 2, 3 km ao norte e a 5, 2 km a leste da usina, junto a uma área de
propriedade particular de 1, 3 km de largura (direção leste-oeste) entre a usina e a fábrica. O cabo de alta tensão deve
passar pela propriedade particular. Veja o mapa:
10
8
6
y
4
2
–3
–2
–1
0
–2
1
x
2
3
–4
–6
–8
–10
O custo de instalação do cabo é de R$ 0,75 por metro através da reserva florestal e R$2,25 por metro na propriedade
privada.
Sua tarefa é achar o tamanho (diâmetro) ótimo do cabo, determinar a rota de menor custo e, finalmente, determinar
o custo total mı́nimo do projeto.
Etapa I: Minimizar o custo por metro relacionado ao tamanho do cabo.
O custo por metro de aquisição do cabo Ca , é diretamente proporcional à espessura do fio, isto é, varia de acordo
com a quantidade de cobre usada por unidade de área da sua seção reta A. O departamento de compras providenciou
às seguintes cifras:
Ca (R$)
0,25
A (mcm2 )
167
248
Cap. 18. Problemas de Máximo e Mı́nimos em Intervalos quaisquer
(a) Usando os dados da tabela, ache uma equação para Ca .
De acordo com a teoria da eletricidade, a resistência do material do cabo causa uma perda de potência resultante
da dissipação de energia em forma de calor. O custo por metro desta perda, Cp , é inversamente proporcional à
área da seção reta, A, do fio. Depois de alguns testes o departamento de engenharia, chegou aos seguintes dados:
Cp (R$)
0,2385
A (mcm2 )
105
(b) Usando estes dados, ache uma equação para Cp .
(c) Defina o custo por metro de cabo adquirido, como função da sua seção reta A. Ache a seção reta Amin , em
mcm2 , que minimiza o custo. Determine este custo mı́nimo C(Amin )
Etapa II: Determinar o caminho de custo mı́nimo e o seu comprimento
O custo total de instalação do cabo, Ci é dado por Ci = 0, 75 w + 2, 25 x, onde w é a distância percorrida na
reserva florestal e x a distância através da propriedade particular.
(d) Usando os dados fornecidos, expresse w como uma função de x.
(e) Minimize Ci em relação à x, especificando o intervalo de variação de x.
(f) Com o valor de x, que fornece o menor custo de instalação, ache w e o comprimento total L = w + x do cabo.
Etapa III: Calcular o custo total do projeto
(g) Combine os resultados das Etapas I e II e ache o custo total mı́nimo do projeto.
Etapa Final: Relatório
(h) Envie um relatório com as suas conclusões e o custo mı́nimo estimado do projeto ao diretor da companhia.
Observação: Um relatório mı́nimo deve incluir respostas justificadas às questões propostas e um gráfico mostrando
o percurso mı́nimo que você encontrou.