Capı́tulo 15
Máximos e Mı́nimos em Intervalos
Fechados
15.1
Motivação
Na Seção 4.1.1, estudamos o problema da caixa, onde querı́amos montar uma caixa recortando retângulos nos quatro
cantos de uma lâmina de plástico e dobrando para cima as bordas obtidas. O problema era determinar o tamanho do
corte a ser feito nos cantos da folha de plástico, a fim de obter a caixa de volume máximo. O volume da caixa é uma
função do tamanho do corte, que representamos por x, e é dado por V = x (20 − 2 x)2 , onde 0 ≤ x ≤ 10.
O problema da caixa é um exemplo tı́pico de problemas de determinação de máximos e mı́nimos de funções
definidas em intervalos fechados. Para estudar e resolver problemas desse tipo precisamos de algumas definições e do
estabelecimento de critérios que permitam determinar facilmente estes pontos.
15.2
Máximos e mı́nimos absolutos
Definição 1
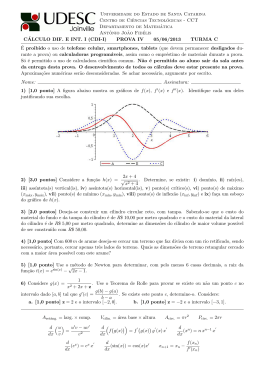
Seja f uma função definida no intervalo fechado [a, b]. Um ponto c pertencente ao intervalo [a, b] é chamado ponto
de máximo absoluto de f ou, simplesmente, ponto de máximo se f (x) ≤ f (c) para todo x em [a, b]. O valor f (c)
é chamado de valor máximo absoluto de f neste intervalo ou, simplesmente, valor máximo de f .
Um ponto d de [a, b] é chamado ponto de mı́nimo absoluto de f ou, simplesmente, ponto de mı́nimo de f
se f (d) ≤ f (x) para todo x em [a, b]. O valor f (d) é chamado valor mı́nimo absoluto de f neste intervalo ou,
simplesmente, valor mı́nimo de f .
Assim, se f (c) é o máximo e f (d) é o mı́nimo de f em [a, b], teremos
f (d) ≤ f (x) ≤ f (c),
para todo x em [a, b]. Os valores máximo e mı́nimo de f são chamados valores extremos de f .
40
valor maximo
30
20
10
–4
–3
–2
–1
1
2
x
3
4
–10
–20
–30
valor minimo
O teorema abaixo garante que toda função contı́nua em um intervalo fechado tem sempre um máximo e um mı́nimo
absolutos.
Teorema dos valores extremos
Seja f uma funcão contı́nua definida em um intervalo fechado [a, b]. Então existem números c e d no intervalo [a,
b], tais que, f(c) é o valor máximo e f(d) é o valor mı́nimo de f em [a, b].
A demonstração deste teorema poderá ser encontrada no apêndice deste volume.
Os exemplos abaixo mostram que se f não é contı́nua ou se o intervalo não é fechado, f pode não atingir valores
máximo e mı́nimo.
196
Cap. 15.
Máximos e Mı́nimos em Intervalos Fechados
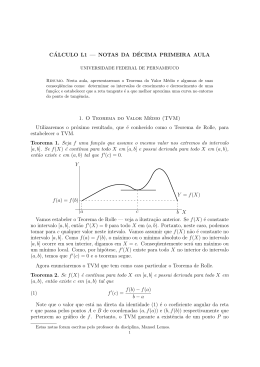
Exemplo 1
Seja f (x) = x2 definida no intervalo [0, 1), isto é, seu domı́nio é um intervalo semi-aberto à direita. Observando o
gráfico de f vemos, claramente, que esta função atinge o mı́nimo em x = 0, porém não atinge um valor máximo. O
candidato a ponto de máximo seria x = 1, porém este ponto não pertente ao domı́nio de f . Como f é crecente neste
intervalo, qualquer que seja o valor de f (x1 ) com x1 < 1, existirá sempre um x2 , tal que x1 < x2 < 1 e f (x1 ) < f (x2 ).
1.2
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.8
0.6
x
1
1.2
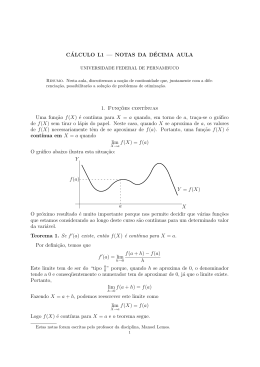
Exemplo 2
A função f definida no intervalo [0, 2] por
{
f (x) =
x ̸= 1
x=1
1
x−1
1
não é contı́nua no ponto x = 1. Seu limite lateral à esquerda lim
x→1−
lim+
x→1
1
= −∞ e seu limite lateral à direita
x−1
1
= +∞. Portanto, esta função não atinge valor máximo nem mı́nimo em [0, 2].
x−1
10
8
6
y
4
2
0
0.2
0.4
0.6
0.8
1
x
1.2
1.4
1.6
1.8
2
–2
–4
–6
–8
–10
Exercı́cio
Esboce o gráfico de uma função definida em [0, 1] que seja descontı́nua e tenha um máximo e um mı́nimo absolutos.
15.2.1
Máximos e mı́nimos locais
Vimos que o teorema dos valores extremos garante a existência de máximos e mı́nimos de uma função contı́nua em um
intervalo fechado [a, b]. A questão natural que se coloca agora é saber onde, exatamente, se localizam estes máximos
e mı́nimos?
Antes de tentar responder a esta pergunta, vamos examinar alguns exemplos.
Exemplo 3
Considere a função f (x) = x3 , que é contı́nua e crescente no intervalo [−1, 1]. Neste intervalo, o valor mı́nimo desta
função é −1 e o valor máximo é 1. Estes valores ocorrem nos pontos x = −1 e x = 1, respectivamente, que são os
extremos do intervalo considerado.
Exemplo 4
Considere a função f (x) = −x2 no intervalo [−2, 2]. Esta função é contı́nua neste intervalo e, portanto, o teorema
dos valores extremos garante a existência de um máximo e de um mı́nimo globais.
Neste caso, o máximo global da função f (x) = −x2 é zero e ocorre em x = 0. O valor mı́nimo é −1 e ocorre em
x = −1 e x = 1.
Exemplo 5
Vamos examinar agora a função f (x) = x3 − 4 x2 − x + 10 definida em [−2, 5]. Veja o seu gráfico traçado a seguir,
à esquerda.
Os valores máximos e mı́nimos desta função ocorrem em 5 e −2, respectivamente, que são os extremos do intervalo.
No entanto, existe um ponto no interior deste intervalo, onde a função atinge um máximo para valores de x, por exemplo,
entre −1 e 1. Da mesma forma, existe um ponto onde f atinge um mı́nimo se considerarmos valores de x entre, por
exemplo 0 e 4. O gráfico seguinte, à direita, da mesma função traçado no intervalo [−1, 3.5], ilustra esta afirmação.
W.Bianchini, A.R.Santos
197
30
10
8
20
6
10
4
2
–2
–1
0
1
2
x
3
4
5
–1
–10
0
1
x 2
3
–2
Estes pontos são ditos máximos e mı́nimos locais, ou, genericamente, extremos locais de f e são caracterizados
na definição a seguir.
Definição 2
Dizemos que um ponto c é um ponto de máximo local ou relativo de f se f(x) ≤ f(c) para todo x suficientemente
próximo de c. Mais precisamente, se esta desigualdade for verdadeira para todo x que esteja no domı́nio de f, em algum
intervalo aberto contendo c. Analogamente, dizemos que d é um ponto de mı́nimo local ou relativo de f se f (d) ≤ f (x),
para todo x suficientemente próximo de d.
A questão que se coloca agora é descobrir algum critério que nos permita identificar com precisão os extremos
relativos de uma função. A reta tangente nos dá uma pista para localizá-los. Observe o diagrama abaixo e conclua o
que é possı́vel afirmar a respeito destes pontos.
À primeira vista, parece ser possı́vel afirmar que, nestes pontos, a reta tangente é horizontal e, portanto, a derivada
da função é zero. No entanto, os exemplos a seguir mostram que extremos relativos podem ocorrer em pontos onde
a função sequer é derivável e que existem pontos, onde a derivada é zero, que não são nem máximo e nem mı́nimo
locais.
Exemplo 6
Examine a função f (x) = 3 − | x − 2 | definida em [1, 4].
3
2.8
2.6
2.4
2.2
2
1.8
1.6
1.4
1.2
1
1 1.21.41.61.8 2 2.22.42.62.8 3 3.23.43.63.8 4
x
O ponto x = 2 é um ponto de máximo relativo desta função (na realidade este ponto é um máximo global para
esta função no intervalo considerado) e f não é derivável neste ponto.
Exemplo 7
Em x = 0, a reta tangente ao gráfico da função f (x) = x3 é horizontal e, portanto, a derivada desta função é zero
neste ponto (prove analiticamente este fato!). No entanto, o ponto x = 0 não é nem ponto de máximo e nem ponto de
mı́nimo local para esta função.
O teorema a seguir esclarece estes fatos.
198
Cap. 15.
Máximos e Mı́nimos em Intervalos Fechados
Teorema: Caracterização dos máximos e mı́nimos locais
Seja f uma função definida em um intervalo aberto (a, b) e derivável em um ponto c de (a, b). Se f ′ (c) ̸= 0 então
f(c) não é máximo nem mı́nimo local de f.
Demonstração:
Se f ′ (c) ̸= 0, então f ′ (c) > 0 ou f ′ (c) < 0. Vamos supor, primeiro, que f ′ (c) > 0. Então, para x suficientemente
próximo de c, temos
f (x) − f (c)
> 0.
x−c
Logo, se x < c , tem-se x − c < 0, o que implica f (x) < f (c). Agora, se x > c, tem-se x − c > 0, o que implica
f (x) > f (c). Assim, c não é extremo relativo de f .
Supondo, agora, f ′ (c) < 0, tem-se (−f )′ (c) > 0. Logo, pelo caso anterior, c não é extremo relativo de (−f ) e
assim, obviamente, c não é ponto de máximo nem mı́nimo relativo de f . (Por quê?)
Observe que o teorema é equivalente a dizer que se f é derivável em (a,b) e c é um ponto de máximo ou mı́nimo local
de f , então, f ′ (c) = 0.
Atenção!!! Cuidado!!! Esta condição é necessária mas não suficiente. Como o Exemplo 7 mostrou, nem sempre é
verdade que se f ′ (c) = 0, então f (c) é um extremo local.
15.3
Determinação dos pontos de máximo e mı́nimo de uma função
Dos exemplos, definições e teoremas estudados na seção anterior podemos concluir que:
Toda função contı́nua definida em um intervalo fechado [a,b] possui um máximo e um mı́nimo global.
O máximo e o mı́nimo para estas funções só podem ocorrer
nas extremidades a e b do intervalo
nos pontos onde a derivada f ′ se anula ou
nos pontos onde a derivada f ′ não existe
Definição 3: Ponto crı́tico
Um ponto c no domı́nio de f é dito um ponto crı́tico de f se f ′ (c) = 0 ou se f ′ (c) não existe.
Assim, para localizar os pontos extremos de uma função contı́nua f definida em [a, b], proceda da seguinte maneira:
1. Determine os pontos crı́ticos de f .
2. Calcule os valores de f em cada um dos seus pontos crı́ticos.
3. Calcule f (a) e f (b).
4. Compare todos os valores e verifique qual o maior e qual o menor.
5. Conclua: o maior dentre estes valores será o máximo absoluto de f e o menor será o mı́nimo absoluto de
f.
15.4
Exemplos
Os exemplos a seguir ilustram o procedimento descrito acima e mostram como podemos usar o Maple para efetuar os
cálculos necessários.
Exemplo 1
Determine os valores máximos e mı́nimos de f (x) = x3 − 3 x2 − 9 x + 3, nos intervalos
(a) [-4, 6]
(b) [-4, 2]
(c) [-2, 4]
W.Bianchini, A.R.Santos
199
Solução Primeiro definimos a função f e calculamos a sua derivada:
>
f:=x->x^3-3*x^2-9*x+3;
f := x → x3 − 3 x2 − 9 x + 3
>
Diff(f(x),x):%=diff(f(x),x);
∂
∂x
(x3 − 3 x2 − 9 x + 3) = 3 x2 − 6 x − 9
Observe que a função f é contı́nua e derivável em todos os pontos da reta. Assim, os candidatos a extremos desta
função são os extremos do intervalo e os pontos onde a derivada se anula. Para determinar estes últimos pontos, basta
resolver a equação f ′ (x) = 0:
>
solve(diff(f(x),x)=0,x);
−1, 3
Nestes pontos crı́ticos os valores de f são, respectivamente
>
f(-1);f(3);
8
−24
Para responder ao item (a) é preciso comparar os valores obtidos acima com os valores de f nas extremidades −4
e 6 do intervalo considerado. Temos
>
f(-4);f(6);
−73
57
Comparando os valores obtidos, concluı́mos que o maior é 57 e o menor é −73, isto é, os pontos de máximo e de
mı́nimo desta função ocorrem nos extremos do intervalo considerado. Assim, o valor máximo de f é 57 e ocorre em
x = 6, que é o ponto de máximo absoluto da função neste intervalo; o valor mı́nimo de f é −73 e ocorre em x = −4,
que é o ponto de mı́nimo absoluto de f em [−4, 6].
Como o ponto crı́tico 3 não pertence ao intervalo [−4, 2], para responder ao item (b) basta comparar os valores de
f no ponto crı́tico −1 e nos extremos −4 e 2 do intervalo.
>
f(2);
−19
Logo, o valor mı́nino desta função, em [−4, 2], é −73. Este valor ocorre em x = −4, que é o seu ponto de mı́nimo.
Da mesma forma, o valor máximo de f , neste intervalo, é 8. Este valor ocorre em x = −1, que é o seu ponto de
máximo.
Para responder ao item (c) vamos calcular os valores de f nas extremidades do intervalo [−2, 4] e compará-los com
os valores de f (−1) e f (3) obtidos acima. Temos
>
f(-2);f(4);
1
−17
Assim, concluı́mos que −1 é o ponto de máximo e 3 é o ponto de mı́nimo de f , em [−2, 4].
• Quais os valores máximo e mı́nimo de f neste intervalo?
Observe o gráfico de f :
>
plot(x^3-3*x^2-9*x+3,x=-4..6);
40
20
x
0
–20
–40
–60
Exemplo 2
√
Determine os pontos de máximo e de mı́nimo de g(x) = | x | no intervalo [−2, 1].
Solução: Como no exemplo anterior, vamos definir a função e achar a sua derivada com o auxı́lio do Maple.
200
Cap. 15.
>
g:=x->sqrt(abs(x));
g := x →
>
√
Máximos e Mı́nimos em Intervalos Fechados
|x|
diff(g(x),x);
1 abs(1, x)
√
2
|x|
Na derivada acima, a expressão abs(1,x ) é a notação usada pelo Maple para a derivada de | x |, isto é, para a
função que vale 1 para x > 0 e −1 para x < 0. Claramente, vemos que a derivada de g não existe no zero e que esta
derivada não se anula em nenhum ponto. Portanto, o seu único ponto crı́tico é o zero. Comparando os valores de g
em −2, 1 (extremos do intervalo) e 0 (ponto crı́tico), concluı́mos que −2 é o ponto de máximo de g e 0 é o ponto de
mı́nimo. A lista de valores de g e o gráfico da função comprovam estas conclusões.
>
g(-2);g(1);g(0);
√
2
1
0
>
plot(g(x),x=-2..1,y=0..sqrt(2),axesfont=[TIMES,ROMAN,8]);
1.4
1.2
1
0.8
y
0.6
0.4
0.2
–2 –1.8
Exemplo 3
Determine os pontos de máximo e mı́nimo de
{
2
h(x) = x + 22
4−x
–1.4
–1 –0.8
x
x≤1
x>1
–0.4
0 0.2 0.4 0.6 0.8
1
no intervalo [−1, 2].
Solução Observando o gráfico desta função, traçado abaixo, concluı́mos que o ponto x = 1 é um ponto crı́tico
para a função h, pois neste ponto a derivada não existe.
>
plot(piecewise(x<=1,x^2+2,x>1,4-x^2),x=-1..2);
3
2.5
2
1.5
1
0.5
–1
–0.6
0
0.20.40.60.8 1 1.21.41.61.8 2
x
De fato, as derivadas laterais em x = 1 são diferentes. Calcule-as e comprove esta afirmação! Assim, para
determinar os extremos desta função, precisamos comparar os valores de h em x = 1 com os valores que ela assume
nas extremidades do intervalo, como fazemos com a ajuda do Maple:
>
h:=x->piecewise(x<=1,x^2+2,x>1,4-x^2):
>
h(-1);h(1);h(2);
3
3
0
Podemos concluir, portanto, que h tem dois pontos de máximo e um de mı́nimo que são, respectivamente, −1, 1 e
2.
15.5
Problemas envolvendo máximos e mı́nimos em intervalos fechados
Problema 1
Um fio com 4 metros de comprimento é cortado em dois pedaços. Com um deles formaremos um cı́rculo e com o
outro um quadrado.
(a) Como devemos cortar o fio para que a soma das áreas limitadas pelo cı́rculo e pelo quadrado seja máxima?
W.Bianchini, A.R.Santos
201
(b) Como devemos cortar o fio a fim de que a soma das áreas seja mı́nima?
(Os dois casos extremos são admitidos, ou seja, é permitido formar com o fio apenas um quadrado ou apenas um
cı́rculo.)
Solução: Dividimos o fio em um ponto qualquer. Seja x o comprimento de um dos pedaços. Obviamente, o
comprimento do outro pedaço será 4 − x. Além disso, pela geometria do problema, os valores possı́veis para x estão
compreendidos no intervalo [0, 4].
Formando um cı́rculo com o pedaço de comprimento x, temos que 2 π r = x, ou seja, r = 2xπ . Assim, a área do
cı́rculo será dada por
π x2
x2
C(x) = π r2 =
=
2
4π
4π
2
e a área do quadrado, por Q(x) = ( 4−x
4 ) . A área total será, portanto, dada por
A(x) = C(x) + Q(x) =
(4 − x)2
x2
+
.
4π
16
Esta função é uma parábola, sendo, conseqüentemente, derivável em qualquer ponto x do intervalo [0, 4]. Assim, os
pontos extremos de A(x ) estarão entre aqueles onde sua derivada se anula ou nas extremidades do intervalo. Abaixo
derivamos a função A(x), calculamos as raı́zes s da equação A′ (x) = 0 e comparamos os valores de A(s), A(0) e A(4).
>
A:=x->x^2/(4*Pi)+(4-x)^2/16:
>
diff(A(x),x);
1 x 1 1
− + x
2 π 2 8
>
s:=solve(%);
π
s := 4
4+π
>
A(s);A(0);A(4);
π
1
π 2
4
+
(4 − 4
)
(4 + π)2
16
4+π
1
4
π
>
simplify(A(s));
4
4+π
4π
Observando estes valores, podemos concluir que o máximo ocorre no ponto x = 4 e o mı́nimo no ponto x = 4+π
.
Assim, para que a área A(x) seja máxima não cortamos o fio e formamos apenas um cı́rculo. Para que a área A(x)
2
4π
. O cı́rculo terá um raio r igual a 4+π
e o quadrado terá um lado
seja mı́nima devemos cortar o fio no ponto x = 4+π
4
de comprimento 4+π .
Problema 2
Considere as parábolas y = x2 − 4 e y = −x2 + 4. Determine as dimensões de um retângulo cujos vértices inferiores
estão sobre a parábola y = x2 − 4 e os superiores sobre a parábola y = −x2 + 4, de tal forma que a área desse retângulo
seja máxima.
Solução Observe no diagrama, que o valor da área depende da posição dos vértices do retângulo.
202
Cap. 15.
Máximos e Mı́nimos em Intervalos Fechados
Devemos determinar as dimensões que fornecerá a área máxima.
Pela simetria da figura ao lado, temos que a área A(x) é dada
por A(x) = 4 x y = −4 x3 + 16 x, para x variando no intervalo [0,
2]. Como A(x) é contı́nua nesse intervalo, o teorema dos valores
extremos garante que esta função tem um máximo absoluto em
[0, 2]. Além disso, este máximo ocorre em um dos extremos do
intervalo ou num ponto crı́tico da função. Como a derivada da
função A(x) é um polinômio do segundo grau, os únicos pontos
crı́ticos de A são os pontos onde a sua derivada se anula. Determinar estes pontos crı́ticos, portanto, é equivalente a resolver
a equação A′ (x) = 0. Vamos, uma vez mais, usar o Maple para
fazer as contas:
>
A:=x->-4*x^3+16*x:
>
4
2
x
0
1
y
–2
–1
x
2
–2
–4
crt:={solve(diff(A(x),x)=0,x)};
crt := {
2√
2√
3, −
3}
3
3
√
O ponto crı́tico que nos interessa é o ponto x = 2 3 3 , pois o outro não pertence ao intervalo [0, 2]. Comparando os
valores da função A neste ponto e nos pontos 0 e 2 (extremidades do intervalo), obtemos:
>
A(0);A(2);A(2/3*sqrt(3));
0
0
64 √
3
9
Portanto, o ponto de máximo para esta função ocorre em x =
√
terá base de comprimento igual a 4 3 3 e altura 16
3 .
2
√
3
3 ,
conseqüentemente, o retângulo de área máxima
Problema 3
Encontre as dimensões do cilindro circular reto de maior volume que pode ser inscrito em um cone circular reto
com raio 7/2 cm e altura 6 cm.
Solução Veja a figura a seguir, onde representamos um corte transversal do cilindro e esquematizamos o problema
proposto.
6-h
r
1
7/2
O volume do cilindro é dado por V = π r2 h. Para expressar o volume em termos de uma única variável, precisamos
de outra equação envolvendo r e h.
12 r
Usando a figura anterior e semelhança de triângulos, temos 67 = 6−h
r , ou seja, h = 6 − 7 . Logo,
2
V (r) = π r2 (6 −
12 r
12 π r3
) = 6 π r2 −
.
7
7
Esta função é contı́nua em [0, 7/2], logo tem um valor máximo absoluto neste intervalo. Vamos, então, derivar a
função V para encontrar os seus pontos crı́ticos:
V := r → 6 π r2 −
>
12 π r3
7
diff(V(r),r);
12 π r −
36
π r2
7
W.Bianchini, A.R.Santos
203
Como esta derivada está definida em toda a reta, os únicos pontos crı́ticos de V são os pontos onde a derivada se
anula. Resolvendo a equação V ′ (x) = 0, obtemos
>
pontos_criticos:={solve(diff(V(r),r)=0)};
pontos criticos := {0,
7
}
3
Comparando os valores de V nos pontos crı́ticos e nos extremos do intervalo, temos
>
V(0);V(7/2);V(7/3);
0
0
98
π
9
Logo, o valor máximo de V será V ( 73 ) =
máximo terá raio r = 37 e altura h = 2 cm.
15.6
98 π
9 ,
que é atingido em r = 73 . Como h = 6 −
12 r
7 ,
o cilindro de volume
Exercı́cios
1. Em cada um dos itens abaixo, decida se a função dada atinge um valor máximo ou um valor mı́nimo ou ambos,
no intervalo indicado. Se necessário esboce um gráfico da função.
(a) f (x) = 1 − x em [-1,1)
1
(f) f (x) = x (1−x)
em [2, 3]
(d) f (x) = x3 + 1 em [-1,1]
(b) f (x) = | x | em (-1, 1)
1
1
(e) f (x) = x2 +1 em (−∞, ∞)
(g) f (x) = x (1−x)
em (0, 1).
(c) f (x) = √1x em (0,1]
2. Em cada um dos itens abaixo, determine
fechado indicado.
(a) f (x) = 3 x − 2 em [−2, 3]
(b) f (x) = 4 − x2 em [1, 3]
(c) g(x) = (x − 1)2 em [−1, 4]
(d) h(x) = x3 − 3 x em [−3, 5]
os valores máximo e mı́nimo atingidos pela função dada, no intervalo
(e) f (x) = x + x1 em [2, 6]
(f) g(x) = | 2 x − 3 | em [1, 2]
x
em [0, 3]
(g) f (x) = x+1
√
(h) f (x) = x 1 − x2 em [−1, 1]
3. (a) Seja f (x) = A x + B. Explique por que os valores máximo e mı́nimo de f , em um intervalo [a, b] qualquer,
devem ocorrer necessariamente nos pontos extremos do intervalo.
(b) Prove que toda função quadrática f (x) = a x2 + b x + c, onde a ̸= 0, tem exatamente um ponto crı́tico em
toda a reta.
(c) Explique por que a função polinomial cúbica pode ter dois, um ou nenhum ponto crı́tico em toda a reta.
Dê exemplos que ilustrem cada um dos casos.
(d) Se f tem um valor mı́nimo em x = c, mostre que a função g(x) = −f (x) tem um valor máximo neste
mesmo ponto.
15.7
Problemas propostos
1. Prove que o retângulo de área máxima e perı́metro dado é o quadrado.
2. Um retângulo de lados paralelos aos eixos coordenados e localizado no primeiro quadrante tem um vértice na
origem, um vértice sobre o eixo x, um vértice sobre o eixo y e o quarto vértice sobre a reta 2 x + y = 100. Qual
a área máxima de tal retângulo?
3. Um campo retangular vai ser fechado com uma cerca e depois dividido ao meio por outra cerca. Se a cerca que
passa pela metade custa R$ 10,00 por metro e a outra R$ 25,00 por metro, encontre as dimensões do campo de
maior área possı́vel que pode ser fechado com um custo de R$ 4800,00.
4. Os pontos A e B são opostos um ao outro nas margens de um rio que mede 3 km de largura. O ponto C está
na mesma margem que B, mas a 6 km de B, rio abaixo. Uma companhia telefônica deseja estender um cabo de
A até C. Se o custo por km do cabo é 25% mais caro sob a água do que em terra, qual o traçado do cabo mais
barato para a companhia?
204
Cap. 15.
Máximos e Mı́nimos em Intervalos Fechados
5. Uma companhia de aviação freta um avião de 50 lugares de acordo com as seguintes condições especificadas no
contrato de afretamento:
(a) Cada passageiro pagará 600 reais se todos os 50 lugares forem vendidos.
(b) Cada passageiro pagará um adicional de 30 reais por lugar não vendido.
Quantos lugares a companhia deve vender para obter renda máxima?
6. Seja f (x) = x2 , para x pertencente ao intervalo [0, 1]. Determine a reta r tangente ao gráfico de f (x), tal que o
triângulo determinado por r, a reta x = 1 e a reta y = 0 tenha a maior área possı́vel.
7. Num certo paı́s, endividado até o pescoço, descobriu-se que a solução de todos os problemas estava na criação
de um combustı́vel para substituir as importações de petróleo. Após muitas pesquisas foi criado o Tomatóleo,
uma mistura de extrato de tomate e gasolina. O litro de extrato de tomate (ET) custa R$ 0,30 e o de gasolina
10
(GS) custa R$ 0,50. Porém, um litro de Tomatóleo, com x litros de ET, dá para um carro médio percorrer 1+x
quilômetros. Determine a quantidade de ET que minimiza o custo por quilômetro.
√
8. Dada a função f (x) = 1 + 18 − 2 x2 , para x ∈ [−3, 3] e o ponto P = (2, 1). Determine a maior e a menor
distâncias de P aos pontos do gráfico de f .
9. Com a finalidade de evitar a construção de prédios muito altos em terrenos pequenos, foi criada na cidade do
Sonho Dourado a seguinte lei: “É obrigatória a existência de uma área livre em torno da área construı́da, com
largura mı́nima de 50cm por metro de altura da construção, medidos a partir dos limites do terreno”. Assim,
em Sonho Dourado, um prédio de 20 m de altura deverá ser construı́do em centro de terreno a uma distância
de, pelo menos, 0, 5x20 = 10 m dos limites do terreno. Supondo que você:
(a) More em Sonho Dourado.
(b) Tenha um terreno de 30 m por 30 m.
(c) Deseja construir um prédio em forma de paralelepı́pedo que tenha volume máximo.
(d) Seja um cidadão respeitador das leis.
Pergunta-se: Quais deveriam ser as dimensões do prédio a ser construı́do?
10. Determine as dimensões do cilindro de área máxima inscrito em um cone circular reto dado.
11. Determine o retângulo de maior área inscrito na região acima da parábola y = x2 e abaixo da parábola y = −2 x2 + 3,
cujos lados são paralelos aos eixos coordenados.
12. Em um terreno com a forma de um semicı́rculo de 25 m de raio, deseja-se construir uma piscina com a forma
de um triângulo retângulo com hipotenusa igual ao diâmetro do cı́rculo e um vértice no semi-cı́rculo. Calcule as
dimensões da piscina de área máxima.
13. Uma janela normanda tem a forma de um retângulo encimado por um semicı́rculo. Se o perı́metro da janela é
2 m, encontre as dimensões da janela para que penetre o máximo de luz possı́vel.
14. Sabendo que a resistência de uma viga retangular é proporcional ao produto da largura pelo quadrado da altura
de sua seção transversal, quais serão as dimensões da viga a ser cortada de um toro cilı́ndrico de raio r para
assegurar a maior resistência possı́vel?
15. Um segmento de reta, de comprimento fixo L, une o vértice de um retângulo ao ponto médio do lado oposto.
Qual a maior área possı́vel de tal retângulo?
16. Uma tipografia dispõe de 8 impressoras, cada uma das quais pode imprimir 3600 cópias por hora. Custa R$ 5,00
para preparar cada impressora para a operação e 10 + 6 n reais para fazer funcionar n impressoras durante uma
hora. Quantas impressoras devem ser utilizadas para imprimir 50000 cópias de um cartaz de forma a obter um
lucro máximo?
17. Um fazendeiro deseja contratar trabalhadores para colher 900 alqueires de grãos. Cada trabalhador pode colher
5 alqueires por hora e recebe em pagamento R$ 1,00 por alqueire. O fazendeiro deve ainda pagar um capataz
a R$ 10,00 por hora para supervisionar a colheita e tem ainda uma despesa adicional de R$ 8,00 com refeições
por trabalhador. Quantos trabalhadores deve contratar de modo a minimizar o custo total? Quanto será então
o custo do alqueire colhido?
W.Bianchini, A.R.Santos
205
18. Uma companhia tem fábricas localizadas (em um sistema de coordenadas adequadamente escolhido) nos pontos
A(0, 1), B(0, −1) e C(3, 0). A companhia planeja construir uma central de distribuição elétrica no ponto P (x, 0).
Qual o valor de x que minimiza o custo de distribuição da energia elétrica produzida?
19. Um gramado circular de 20 m de raio é circundado por um passeio, e uma lâmpada é colocada no cimo de
um poste fincado no centro do gramado. A que altura deve ser colocada a lâmpada para que o passeio receba
iluminação máxima?
Observação: a intensidade de iluminação de uma superfı́cie é dada por I = k sen(θ)
onde D é a distância da fonte
D2
de luz à superfı́cie, θ é o ângulo segundo o qual a luz atinge a superfı́cie e k é uma constante positiva.
20. Cinco placas de metal retangulares medem 210 cm por 336 cm cada. Cortam-se pedaços quadrados iguais de
cada um de seus cantos, e as abas resultantes devem ser dobradas para cima e soldadas, de modo a formar cinco
caixas sem tampa. Os vinte pequenos quadrados retirados são reunidos em grupos de quatro e soldados para
formar cinco quadrados maiores, que por sua vez são soldados de modo a formar uma caixa cúbica sem tampa,
de modo que nenhum material é desperdiçado. Qual o tamanho do corte para que o volume total das seis caixas
assim formadas seja o maior possı́vel?
21. Deve-se construir uma pista de corrida em forma de dois trechos retilı́neos, paralelos e de igual comprimento,
unidos por dois semi-cı́rculos nas extremidades. O comprimento da pista (uma volta completa) deve ser de 5
km. Quais são as dimensões da pista que maximizarão a área retangular interna?
22. Um objeto é arrastado num plano horizontal por uma força que age ao longo de uma corda atada a ele. Se a
corda faz um ângulo θ com o plano, então a magnitude da força é dada por
F =
µW
,
µ sen θ + cos θ
onde µ é uma constante positiva chamada coeficiente de fricção e 0 ≤ θ ≤
quando tg θ = µ
15.8
π
2.
Mostre que F é minimizada
Para você meditar: O feirante de Caruaru
Um vendedor foi à feira de Caruaru com sua balança de dois pratos defeituosa, pois tinha um braço mais curto do
que o outro. Para compensar isto, ao atender os fregueses, passou a usar, sucessivamente, os dois lados para pesar a
mercadoria. Por exemplo, se alguém desejava dois quilos de açúcar, o vendedor lhe dava um quilo com excesso (pesado
usando-se um dos pratos da balança) e um quilo com falta (pesado usando-se o outro lado).
• Quem ganha com este processo?
Sugestão: Use a Lei das alavancas para obter uma relação entre o peso da mercadoria e o tamanho dos braços da
balança.