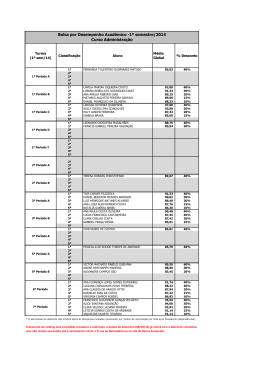
MATEMÁTICA FINANCEIRA HP E EXCEL Prof. Gilberto de Castro Timotheo
Página 1
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Sumário
Conceitos e Convenções ...................... 3
Conceitos ................................................ 3
Convenções............................................. 3
Convenções aplicadas a HP e
EXCEL ..................................................... 4
Conhecendo a HP.................................. 5
Princípio de funcionamento............... 6
Regimes de Capitalização ................... 8
Juros Simples ........................................ 10
Juros compostos.................................... 13
Classificação das Taxas ....................... 14
Operações de Desconto........................ 18
Fluxo de Caixa Uniforme .................... 24
Fluxo de Caixa Irregular..................... 28
Referências............................................. 31
Prof. Gilberto de Castro Timotheo
Página 2
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Matemática Fianceira
Conceitos e Convenções
Conceitos
¾ “A matemática financeira é um
conjunto de técnicas e formulações
matemáticas, com o objetivo de
analisar
situações
financeiras
envolvendo o valor do dinheiro no
tempo. Em qualquer operação
financeira, existem dois fatoreschaves: dinheiro e tempo. O objetivo
da matemática financeira é analisar
como os recursos financeiros se
modificam ao longo do tempo.
¾ O valor do dinheiro muda no tempo,
uma vez que o possuidor do dinheiro
pode aplicá-lo e obter uma taxa de
remuneração
pelo
capital.
A
remuneração do capital no tempo é
chamada de juros e pode ser encarada
como um direito inerente ao capital. O
juro é a remuneração paga a quem
possui os recursos financeiros.
¾ Entende-se por capital qualquer valor
expresso em moeda e disponível para
consumo
ou
investimento
em
determinada data. Neste livro,
usamos "$" como símbolo de uma
moeda genérica, sendo que os
conceitos de matemática financeira se
aplicam para qualquer moeda.
¾ Ao se dispor a aplicar recursos, o
detentor do capital espera receber
uma taxa de juros, que depende de
diversos fatores, entre eles o risco da
operação (probabilidade de perda do
capital), a inflação (desvalorização do
poder aquisitivo da moeda), a liquidez
do investimento (prazo) e o valor do
capital aplicado. O juro é sempre
proporcional ao valor do capital
Prof. Gilberto de Castro Timotheo
aplicado (ou emprestado) e ao tempo
de duração da operação financeira.
¾ A taxa de juros é a razão entre os
juros recebidos (ou pagos) no fim de
um período de tempo e o capital
inicialmente empregado. A taxa de
juros sempre está relacionada com
uma unidade de tempo (dia, semana,
mês, semestre, ano etc.). Ela pode ser
indicada em forma de fração ou
porcentagem do capital que a gerou.”
(Silva, 2005).
Convençoes
9 Capital
Também denomido “Principal” é o valor
inicial de qualquer operação, seja ela de
financiamento ou investimento.
9 Juros
È o valor recebido pelo detentor do
capital pela abstenção de seu uso em
um período de tempo.
9 Prazo
Período pelo qual o capital vai
permanecer aplicado ou emprestado é
medido em dias, meses, anos etc.
9 Montante
É o volume do capital acrescido dos
juros ao final de determinado período.
9 Amortização ou Resgate
Página 3
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
É o valor pago do capital investido ou
emprestado em parcelas ou ao
vencimento da operação(prazo final).
9 Pagamentos ou Recebimentos
São parcelas compostas pelo juros
somente ou formada pelos juros +
(amortização ou resgate).
9 Período ou ano Comercial
Representa um perído de tempo
representado por 360 dias considera-sae
o mês de 30 comercial dias.
9 Perído ou ano civil
Representa um perído de tempo
compreendido de 365 anos normais e
366 para anos bissexto, considera-se os
dias efetivamente transcorridos
Convenções aplicadas a HP e Excel
9 Valor persente- VP - (HP PV)
É o período de duração de um
investimento ou empréstimo.
9 Taxa de juros - i - (HP – i)
É a razão entre os juros(pagos ou
recebidos) e o capital, expressa de forma
unitária(0,01) ou percentual (10% representando a décima parte de 100
unidades)
9 Pagamento - PGTO - (HP –
PMT)
Também chamado de
prestação(recebimento ou pagamento)
com valores constantes distribuídos
periodicamente no período da operação
9 Fluxo de caixa - Fc - (HP – Cf
(cash flow))
É o conunto e entradas e saidas de
dinheiro (caixa) de um indivíduo ou
empresa ao longo do tempo. Tem como
convenção a representatividade em uma
reta e os pagamentos e recebimentos
representados nesta reta com sentidos
contrários(para baixo e para cima)
Representa o capital investido ou
aplicado no momento atual.
receb
final
9 Valor futuro – VF - (HP – FV)
Representa o capital acumulado
acrescido dos respectivos juros em
determinado prazo.
Cf0
PGTO
9 Prazo- n - (HP – n)
Prof. Gilberto de Castro Timotheo
Página 4
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
9 Taxa interna de retorno – TIR
- (HP - IRR – internal rate of
return)
É a taxa que equaliza as entradas e
saídas de um fluxo de caixa
9 Valor presente líquido – VPL (HP – NPV)
È o valor presente de um série de
pagamentos a uma taxa mínima de
atratividade deduzindo deste o
investimento inicial.
9 Data focal – D f
È uma data compreendida dentro de
um fluxo de caixa na qual queremos
calcular o valor de nossas entradas e
siadas (valor presente).
Conhecendo a HP
9 Controle de casas decimais
Digitamos o número 49,23453,
Ex 1 – se digitarmos a tecla
o número “2” teremos:
f
e
f
e
No visor - “49,23”
Ex 2 – se digitarmos a tecla
o número “3” teremos:
No visor - “49,235”
Desta forma podemos regular as casas
decimais no intervalo de 0 a 9 casas,
considerando que o arredondamento
segue o seguinte critério: entre 0 e 4 o
arredondamento é para baixo e de 5 em
diante o arredondamento é para cima.
9 Pontuação
Originalmente a HP 12C usa o
formato “,” e “.” (ex: 2,000.32)
f
Esta tecla aciona todos os
comandos grafados na cor “laranja”
Para alteramos, basta
desligarmos a calculadora pressionando
a tecla “ on “ e em seguida presionamos
a tecla “ .”, mantendo-a apertada
pressionamos a tecla “ on “, soltando
esta última primeiro e em seguida a
tecla “ .”.
g
Esta tecla aciona todos os
comandos grafados na cor “azul”
Prof. Gilberto de Castro Timotheo
Página 5
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
9 Troca de sinal
9 Teclas de armazenamento e
recuperação de dados
Originalmente quando teclamos um
número ele assume o valor positivo,
para alterarmos está condição
digitamos o número e em seguida a
tecla “CHS”
A HP possui duas teclas destinadas a
armazenar dados durante cálculos, são
elas:
¾ “STO” - para armazenar, com
possibilidade de um fluxo de 20
unidades ( de 0.1 a 9)
Príncipios de funcionamento
A HP funciona com o sistema de pilhas
de armazenamento conforme abaixo:
EX:
T
0
0
0
0
visor
Z
0
0
0
0
20
STO
0.1
Y
0
5
5
0
25
STO
0.8
X
5
5
2
0
12
STO
2
13
STO
9
visor
TC
5
2
enter
-
¾ “RCL” - para recuperar os
dados armazenados na tecla
“STO”
Temos a expressão: ( 3 x 4 ) + (5 x 6)
EX: recuperando os dados do exemplo
anterior:
7
T
0 0
0 0
0
0
0
0
0
Z
0 0
0 0
0
12
12 0
0
Y
0 3
3 0
12 5
X
3 3
4 12 5
TC
3
4 x
enter
5
5
enter
Prof. Gilberto de Castro Timotheo
visor
0.1
20
RCL
0.8
25
5
12 0
6
30 42 7
6
RCL
2
12
6
x
÷
RCL
9
13
+
42
RCL
7
Página 6
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
9 Limpeza dos registradores
Para se limpar os registradores é
necessario teclar f
“REG”.
f
e
“FIN” , este procedimento
garante a exatidão do resultado da
operação a ser realizada.
Para limpar o visor tecle “CLX”
9 Tratamento de data
9
9 Operações com datas
DATE
Esta tecla permite encontrar uma data
futura ou passada a partir da contagem
de dias.
EX: Calcule em que dia vence um título
pré fixado para 265 dia a contar de
24.11.2007.
Certifique-se que no visor está D.MY
visor
A HP permite dois formatos de data:
D.MY ( dia mês ano)
Para colocar a calculadara neste
modulo tecle
“D.MY”, no visor
g
24.112007
265
enter
g
DATE
15.08.2008
em tamanho reduzido na parte inferior
direito aparecerá D.MY .
EX: A data 24.11.2007 deve ser
digitada assim:
24.11207
EX: Um título foi aplicado a 210 dias
atrás, como sendo hoje dia 14.11.2207,
gostaria de saber qual a data da
aplicação?
visor
M.DY (mês dia ano)
24.112007
Para colocar a calculadara neste
modulo tecle
“M.DY”, no visor
210
g
em tamanho reduzido na parte inferior
direito aparecerá M.DY.
EX: a data 24.11.2007 deve ser digitada
conforme abaixo:
g
enter
CHS
DATE
28.04.2007
11.242007
Prof. Gilberto de Castro Timotheo
Página 7
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
¾ Operações com juros simples
ou compostos
DYS
Calcula o número de dias exato entre
duas datas.
Ao teclarmos “STO” e em seguida
“EEX” aparecerá na parte inferior
diredo visor a letra “C”, isto
significa que todos os cálculos são
feitos a juros compostos.
EX:
visor
24.112007
28.042007
“STO” “EEX”
enter
DYS
g
Se teclarmos “STO” e em seguida
“EEX” o “C” desaparecerá do visor
e então nossos cálculos estarão
sendo realizados ajuros simples.
- 210
EX:
¾ Operações algébricas
Soma
10+4
10
4
Subtração
10-4
10
4
Multilicação
10x4
10x4
10
4
rediciação
10¼
50.000,00
PV
5
i
0,5
n
-
x
10
4
Potenciação
EEX “C” desativado
FV
-51.250,00
10
4
Divisão
+
STO
÷
STO
EEX “C” ativado
50.000,00
PV
5
i
0,5
n
FV
-51.234,75
10
4
Prof. Gilberto de Castro Timotheo
Página 8
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Regimes de Capitalização
O gráfico abaixo representa a tabela1.
Os juros auferidos em um processo de
investimento ou empréstimo, pode ser
calculado através de dois regimes
diferentes : Juros Simples ou Juros
Compostos.
Na capitalização por juros simples o
capital inicial é a base do calculo dos
juros periódicos.
Na capitalização por juros compostos a
base de calculo passa a ser o capital
inicial acrescido dos juros dos períodos
anteriores, este sistema é tambem
chamado de capitalização exponencial.
Abaixo veremos as tabelas 1 e gráfico 1
- juros simples, tabela 2 e gráfico 2 –
juros compostos, e um gráfico 3
mostrando a comparação entre os dois
regimes.
Gráfico 1. Crescimento do dinheiro a
juros simples.
Tabela 1. Crescimento do dinheiro a
juros simples.
Ano Capital
inicial
PV
I%
Juros
ao ano
Capital
final FV
1
100,00
10
10,00
110,00
2
110,00
10
11,00
121,00
3
121,00
10
12,10
133,10
4
133,10
10
13,31
146,41
5
146,31
10
14,64
161,05
Ano Capital
inicial
PV
I%
Juros
ao ano
1
100,00
10
10,00
110,00
2
110,00
10
10,00
120,00
3
120,00
10
10,00
130,00
4
130,00
10
10,00
140,00
5
140,00
10
10,00
150,00
Prof. Gilberto de Castro Timotheo
Capital
final FV
Tabela 2. Crescimento do dinheiro a
juros compostos.
Página 9
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
O gráfico abaixo representa a Tabela 2.
Gráfico 3. Comparativo entre os regimes
de capitazação
Juros Simples
No regime de juros simples, a taxa vi
insidir sempre sobre o capital inicial,
não existindo cobrança sobre os juros
gerados anteriormente, desta forma o
juros produzido por período é constante
e proporcional ao capital.
“A taxa de juros e o prazo devem estar
na mesma base temporal” (Silva, 2005).
Gráfico 2. Crescimento do dinheiro a
juros compostos.
Fórmula:
Juros
Abaixo gráfico comparativo enre os dois
regimes.
Onde : Pv = capital inicial
I = taxa de juros
N = prazo
J = juros calculados
FV (capital final ou montante)
FV = PV + J
FV = PV + (PV x i x n)
FV = PV x (1 + i x n)
Prof. Gilberto de Castro Timotheo
Página 10
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
1. Determinar o valor de resgate de uma
aplicação de $ 45.000,00, por um prazo de 8 trimestres, a uma taxa de
1,5% a.m.
2. Determinar o principal que, à taxa de
2% a.s., produz juros de $ 2.000,00 ao
final de 4 anos.
¾ Exercícios resolvidos
Ex:
Determine o valor de resgate de um
capital que, aplicado por seis
semestres á taxa de 30% a.a., rende
$60.000,00 de juros.
3.
Determinar a taxa mensal de juros
que faz com que um capital investido
por 6 bimestres renda juros iguais à
metade do valor aplicado.
4.
Determinar quantos meses são
necessários para quintuplicar um
capital aplicado a 8% a.s.
5.
Calcular os juros recebidos por um
investidor ao aplicar $ 10.000,00
durante 6 meses e 10 dias, a uma taxa
de 1% a.m. Obs.: Assumir o mês com
30 dias.
6.
Determinar a taxa semestral de juros
paga por um mutuário que tomou um
financiamento de $ 20.000,00 por um
prazo de 15 meses e pagou $ 5.000,00 de
juros.
7.
Um professor realizou um
investimento no Banco "A", por um
prazo de 24 meses, a uma taxa de
22% a.a. No vencimento, resgatou a
aplicação e investiu todo o montante
no Banco "B", a uma taxa de 25%
a.a., por um prazo de 32 meses,
retirando ao final um valor de $
550.000,00. Qual foi o valor aplicado
inicialmente no Banco "A"?
8.
Um empresário necessitará de $
10.000,00 no fim de 5 meses e $
18.000,00 no final de 9 meses. Ele foi
aconselhado
a
aplicar
uma
determinada quantia financeira hoje,
para fazer face aos pagamentos
futuros. Determinar o valor do
principal necessário para que o
empresário possa honrar seus dois
Solução:
i = 30% a.a
n = 6 semestres = 3 meses
juros = 60.000,00
PV = ?
FV = ?
Juros = PV x i x n
PV =
=
= 66.666,67
FV = PV + Juros
FV = 66.666,67
126.666,67
¾ Exercícios
+
60.000,00
=
Propostos
Obs.: Todos os exercícios assumem regime
de juros simples.
Prof. Gilberto de Castro Timotheo
Página 11
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
compromissos em suas respectivas
datas, sabendo-se que o banco irá
remunerar o investimento a uma
taxa de 2% a.b.
9. Um indivíduo deve $ 500,00 no prazo
de 8 meses e $ 1.200,00 no prazo de
18 meses. Qual é o valor do
pagamento único a ser efetuado hoje
que liquidaria os dois débitos,
sabendo que a taxa de juros é 15%
a.a.?
10. Um pai comprou por $ 20.000,00 um
título de renda fixa com prazo de 36
meses à taxa de 18% a.a. Um ano
depois, propôs vender o título para
seu filho. Determinar o valor justo
da venda, sabendo-se que a taxa de
juros no mercado é 23% a.a. Caso o
título seja vendido pelo valor justo,
qual será a taxa anual de juros
recebida pelo pai no período em que
ficou com o título?
11. Uma pequena empresa contrai hoje
uma dívida de $ 18.000,00 com prazo
de 9 meses. A empresa planeja pagar
ao credor $ 8.000,00 daqui a 6 meses
para reduzir o valor do pagamento no
vencimento. Caso o credor concorde
em receber esse valor no sexto mês,
quanto faltará a ser pago no
vencimento, sã bendo que a taxa de
financiamento é 3% a.t.?
12. A empresa SoDevo S.A. comprou
um equipamento cujo valor a vista
era $ 50.000,00. A empresa pagou 10%
de entrada e concordou em financiar o
restante a uma taxa de juros de 3%
a.m. Se a empresa pagar ao banco $
9.000,00 nove meses após a compra e
$ 15.000,00 quinze meses após a
compra, quanto precisará pagar para
liquidar o financiamento dois anos
depois da compra?
de juros de 1,8% a.m. Seis meses depois,
podendo dispor do mesmo capital a juros de
1,2% a.m., saldou seu débito referente ao
principal e juros através de um novo
financiamento a taxas mais vantajosas.
Sabendo-se que o total de juros pagos nos
dois financiamentos foi de $ 12.048,00,
determinar
o
prazo
do
segundo
financiamento e a taxa média mensal
paga pelo comerciante nos dois
empréstimos
“Exercicios extraidos de (Silva, 2005)”
Gabarito
1.
$ 61.200,00
2.
$ 12.500,00
3. 4,17% a.m.
4. 300 meses
5.
$ 633,33
6.
10% a.s.
7. $ 229.166,67
8. $ 26.037,57
9. $ 1.434,14
10. $ 21.095,89 e 5,48% a.a.
11. $ 11.393,58
12. $47.417,92
13. 10 meses e 1,51% a.m.
13.
Um comerciante
contrai
um
financiamento de $ 50.000,00 a uma taxa
Prof. Gilberto de Castro Timotheo
Página 12
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Juros Compostos
de 5% a.m., com prazo de 3 trimestres.
Comparar os resultados com o do
Exemplo 2.1.
Solução:
PV = 50.000,00
Neste regime, a taxa incide sobre o
saldo acumulado do período anterior
(capital inicial + juros dos períodos
anteriores), é o mais utilizado sendo
a base de cálculo dos empréstimos e
investimentos.
n = 3 trimestres = 9 meses
i = 5% a.m.
Juros = ?
FV = ?
FV = PV x (1+ i)n = 50.000,00 x (l +
5%)9 = 77.566,41
Fórmula
Juros 1º período
FV PV J PV PV x i PV x 1 i mês
PV
Juros Mensais
FV
1
50.000,00
5% x 50.000,00 =
2.500,00
52.500,00
2
52.500,00
5% x 52.500,00 =
2.625,00
55.125,00
3
55.125,00
5% x 55.125,00 =
2.756,25
57.881,25
4
57.881,25
5% x 57.881,25 =
2.894,06
60.775,31
5
60.775,31
5% x 60.775,31 =
3.038,77
63.814,08
6
63.814,08
5% x 63.814,08 =
3.190,70
67.004,78
7
67.004,78
5% x 67.004,78 =
3.350,24
70.355,02
8
70.355,02
5% x 70.355,02 =
3.517,75
73.872,77
9
73.872,77
5% x 73.872,77 =
3.693,64
77.566,41
Juros 2º período
J 2 FV1 x i PV x 1 i x i FV2 FV1 J2 PV x 1 i PV x 1 i x i PV x 1 i ² Este cáuculo é repetido em todos os
períodos da operação , donde para
um capital aplicado (PV), a uma
taxa de juros i, por um prazo n, é
dado por:
¾ Exercícios Resolvidos
Resolvendo pela HP
Determinar os juros e o valor de
resgate de um empréstimo de $
50.000,00, com taxa de juros compostos
Prof. Gilberto de Castro Timotheo
Página 13
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
50.000
PV
9
n
5
i
FV
-77.566,41
¾ Exercícios
sabendo que o banco remunera a
uma taxa de 6% a.t.
7.
Um banco vendeu títulos de sua
emissão por $ 98.500,00. O título
vence em 100 dias, com valor de
resgate de $ 100.000,00. Determinar
a
taxa
anual
da
operação,
considerando o ano civil.
8.
Uma pequena empresa deseja
reestruturar
suas
dívidas.
Atualmente, ela tem três obrigações,
nos valores de $ 30.000,00,
$
50.000,00 e $ 80.000,00, com
vencimentos em 50, 70 e 90 dias,
respectivamente. Ela deseja trocar os
três pagamentos por um único daqui a
120 dias. Determinar o valor desse
pagamento, sabendo-se que a taxa de
juros de mercado é de 30% a.a. (ano
comercial).
9.
Um empresário comprou um veículo
no valor de $ 30.000,00, dando uma
entrada de $ 5.000,00, ficando com
uma prestação de $ 15.000,00 para 3
meses e outra para 6 meses.
Determinar o valor da última
prestação, sabendo-se que a taxa de
juros é 3% a.b.
10.
Um aposentado comprou um
certificado de depósito bancário
(CDB) que paga $ 100.000,00 daqui a
182 dias. Determinar o valor de
emissão, para que a taxa de juros na
operação seja 17% a.a. (ano
comercial).
11.
Uma empresa contraiu um
financiamento que deve ser liquidado
com um pagamento único no final de
15 meses. A taxa de juros do banco é
3,5% a.m., desdobrada em dois
componentes: (a) uma taxa de 2,5%
a.m. cobrada de forma postecipada; e
(b) uma taxa antecipada (em
porcentagem do valor financiado),
cobrada a vista e a título de tarifa de
Propostos
Obs.: Todos os exercícios assumem regime de
juros compostos.
1.
Determinar o valor de resgate de um
investimento de $ 20.000,00, aplicado
a uma taxa de juros de 3,2% a.m.,
por um prazo de 4 semestres.
2.
Calcular o investimento necessário
para se produzir um montante de $
43.000,00, a uma taxa de juros de
16,5% a.a., daqui a 187 dias. Fazer os
cálculos
considerando
o
ano
comercial e o ano civil.
3. Determinar o prazo necessário para um
capital triplicar, a uma taxa de 25% a.a.
4.
Qual é a taxa semestral de juros que
produz um montante de $ 79.000,00
a partir de um investimento de $
50.000,00 no fim de 10 anos?
5.
Determinar o valor hoje das
seguintes obrigações: $ 3.000,00
devidos hoje, $ 5.000,00 devidos em 5
meses e $ 9.000,00 devidos em 7
meses, com juros de 3,5% a.m.
6.
Um estudante deseja investir uma
quantia que lhe permita resgatar $
50.000,00 no final de 12 meses e $
75.000,00 no final de 24 meses.
Determinar o valor do investimento,
Prof. Gilberto de Castro Timotheo
Página 14
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
abertura de crédito. Determinar o valor da taxa antecipada para que o
custo total do financiamento seja 3,5%
a.m.
“Exercicios extraídos de (Silva, 2005)”
períodos diferentes de tempo, produzem
sobre um mesmo capital inicial o
mesmo montante no final da operação a
juros simples.
EX:
¾ Gabarito
1. $42.593,44
Taxa ao ano = 2 x taxa ao semestre=4 x
taxa ao trimestre=6 x taxa ao bimestre=
12 x taxa mensal= 360 x taxa dia.
2. $39,720,60(ano comercial) e
$39.763,79(ano civil)
3. 4,92 anos
4. 2,31% a.s.
5. $14.283,78
6. $86.660,61
7. 5,67% a.a.
8. $165.194,10
¾ Equivalentes
Duas taxas são classificadas como
proporcionais
quando
dadas
em
períodos diferentes de tempo, produzem
sobre um mesmo capital inicial o
mesmo montante no final da operação a
juros compostos.
EX:
(1+ )=
9. $11.638,14
=
=
=
=
10. $92.369,43
11. 13.55%
Classificação das taxas de juros
Ex: Determinar a taxa mensal
equivalente a: (a) 6% a.t.; (b) 24% a.s.; (c)
36% a.a.
Solução:
¾ Taxas Proporcionais e
Equivalentes
¾ Proporcionais
Duas taxas são classificadas como
proporcionais
quando
dadas
em
Prof. Gilberto de Castro Timotheo
(a) (l + it)1/3 -1 = (1 + 6%)1/3 - l =
1,96% a.m.
(b) (l + i,)1/6 - 1 = (l + 24%)
3,65% a.m.
1/6
- l =
Página 15
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
(c) (l + ia)1/12 - 1 = (! + 36%)1/12 - l =
2,60% a.m.
(l + ib)3/2 - 1 = (1 + 2%)3/2 - l = 3,01% a.t.
100,00 CHS
PV
2
i
100,00 CHS
PV
0
PMT
6
i
3 [ENTER] 2 [/]
n
0
PMT
1 [ENTER] 3 [/]
n
FV
103,01
FV
101,96
Ex: Determinar a taxa diária equivalente
a 25% a.a., assumindo ano civil.
100,00 CHS
PV
24
i
0
PMT
1 [ENTER] 6 [/]
n
FV
103,65
Solução:
100,00 CHS
PV
36
!
0
PMT
1 [ENTER] 12 [/]
n
FV
102,60
Logo, as taxas equivalentes são
iguais a 1,96% a.m., 3,65% a.m. e 2,60%
a.m. Vale ressaltar que os valores das
taxas equivalentes são inferiores aos das
taxas proporcionais do Exemplo 4.3, uma
vez que as taxas proporcionais (juros simples) crescem mais rápido do que as taxas
equivalentes (juros compostos) quando n é
fracionário.
Ex: Determinar a taxa
trimestral equivalente a 2% a.b.
(l + i )1/365 - 1 = (1 + 25%)1/365 - l = 0,06%
a.d.
Ex:
Determinar
a
taxa
diária
proporcional a 25% a.a., assumindo ano
civil.
0,07% a.d.
¾ Taxas Nominais e Efetivas
¾ Nominais
São as taxas que aparecem descritas
nos contratos, enunciados, e estão
representadas em um determinado
perído de tempo. Se capitalizadas por
este mesmo período de tempo, dizemos
Solução:
Prof. Gilberto de Castro Timotheo
Página 16
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
que também é efetiva
exemplificadas abaixo:
¾ Exercícios
comforme
• 17% a.a., capitalizados anualmente;
• 12% a.s., capitalizados emestralmente;
Propostos
1. Determinar as taxas mensal e
trimestral proporcionais a 24% a.a.
• 5% a.t., capitalizados trimestralmente;
2. Determinar as taxas mensal e
trimestral equivalentes a 18% a.a.
• 3% a.b., capitalizados bimestralmente;
3.
• 1,5% a.m., capitalizados mensalmente
Por outro lado se taxa nominal ou a
taxa apresentada no contrato,
enunciado, está em uma unidade de
tempo e é capitalizada em outra unidade
de tempo, a taxa efetiva será aquela
apresentada após o processo de
capitalização, sendo assim diferente da
taxa nominal.
Podemos dizer que a taxa efetiva
representa aquela utilizada nos cálculos
financeiros e representa o custo ou
rendimento da operação.
Portanto devemos sempre transformar
as taxas nominais em taxas efetivas pelo
regime de juros simples e então
promover a capitalização.
EX:
17% a.a., capitalizados semestralmente ,
taxa nominal anual.
i=
semestral
= 8,5% a.s - Taxa efetiva
(1 + 8,5)² - 1 = 17,72% a.a. – Taxa efetiva
anual
Determinar a taxa anual
equivalente
a
48%
a.a.,
capitalizados bimestralmente.
4. Determinar a taxa bimestral
equivalente a 12% a.s.
5.
Determinar as taxas mensal,
bimestral e trimestral equivalentes
a
12%
a.a.,
capitalizados
semestralmente.
6.
Determinar a taxa anual (ano
comercial) equivalente à taxa de 32%
a.a. (ano civil).
7.
Determinar o montante acumulado
por um investidor que aplicou $
80.000,00 por cinco trimestres a 21%
a.a., capitalizados bimestralmente.
8. Um investidor aplicou $ 130.000,00
por dois anos a uma taxa de 18%
a.a., capitalizados trimestralmente.
Qual é o montante esperado ao final
da aplicação?
9. Determinar o investimento necessário
para produzir um montante de $
75.000,00 ao final de 9 bimestres à
taxa de 24% a.a., capitalizados
mensalmente.
10. Um investidor quer resgatar $
75.000,00 daqui a 8 meses. Qual deve
ser o valor de sua aplicação hoje,
sabendo-se que a taxa de juros é 18%
a.a., capitalizados bimestralmente.
“Exercícios extraidos de (Silva, 2005).”
™
Prof. Gilberto de Castro Timotheo
Página 17
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
¾ Gabarito
1. 2,00% a.m. e 6,00% a.t.
2. 1,39% a.m. e 4,22 a.t.
3. 58,69% a.a.
4. 3,85 a.b.
5. 0,98% a.m., 1,96% a.b. e 2,96%
a.t.
¾ Desconto Racional
O desconto racional (desconto "por
dentro") pode ser calculado no regime de
juros simples, incidindo a taxa de juros
sobre o valor presente. A taxa de juros (i)
também é chamada de taxa de desconto
racional simples. O Valor Futuro (FV),
Valor Presente (PV) e Desconto (D)
podem ser obtidos por meio das
seguintes equações:
6. 31,50% a.a.
7. $103.548,21
8. $184.873,08
9. $52.511,95
10. $66.636,53
Operações de Desconto
¾ Conceito
È a importância ou valor deduzidos de
um título com prazo de vencimento e
valor
nominal
definidos,
para
pagamento ou resgate antecipado deste
título.
O desconto pode ser
através da
incidência da taxa sobre o valor futuro
do título ( desconto “por fora”)
denomidado desconto comercial ou
bancário, ou sobre o valor presente do
título (desconto “por dentro”) também
chamado de desconto recional.
Ex: Uma loja procurou um banco para
descontar uma nota promissória com
valor nominal de $ 65.000,00, com
vencimento em 8 meses. Determinar o
valor recebido pela loja e o desconto
aplicado, sabendo-se que o banco cobra
uma taxa de desconto racional simples de
3% a.m.
Solução:
FV = 65.000,00
n = 8 meses
i = 3% a.m.
PV = ?
¾ Capitalização Simples
Prof. Gilberto de Castro Timotheo
Página 18
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
vencimento em 8 meses. Determinar o
valor recebido pela loja e o desconto
aplicado, sabendo-se que o banco cobra
uma taxa de desconto comercial
simples de 3% a.m. Qual é a taxa
mensal de juros (desconto racional
simples) implícita na operação?
= 52.419,35
D = FV – PV
D = 65.000,00 – 52.419,35 = 12.580,65
Solução:
FV = 65.000,00
¾ Desconto
Bancário
Comercial
ou
n = 8 meses
d = 3% a.m.
O desconto comercial ou bancário
(desconto "por fora") é calculado no regime
de juros simples, multiplicando-se a taxa
de desconto pelo valor futuro (ou valor
nominal) e pelo prazo da operação. No
desconto "por fora", a taxa de juros (i), que
incide sobre o valor presente, é sempre
superior à taxa de desconto (d), que
incide sobre o valor futuro. O Valor
Futuro (FV), o Valor Presente (PV) e o
Desconto (D) podem ser obtidos por meio
das seguintes equações:
D=FVxixn
PV = ?
i =?
D = FV x d n
D = 65.000,00 x 3% * 8
D = 15.600,00
PV = FV – D
PV = 65.000,00 – 15.600,00
PV = 49.400,00
D = FV – PV
PV= FV-D
PV= F V - F V x i x n
A taxa de desconto implícita na
operação é maior que os 3% nominais.
FV = PV x (1 + i x n)
65.000,00=49.400,00 x (1 + i x 8)
PV = FV x (l – i x n)
Ex: Uma loja procurou um banco para
descontar uma nota promissória com
valor nominal de $ 65.000,00, com
Prof. Gilberto de Castro Timotheo
i = 3,95% a. m.
¾ Capitalização Composta
Página 19
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
¾ Desconto Racional
O mecanismo de desconto racional
("por dentro") composto está relacionado
diretamente com o tema estudado no
Capítulo 3. No desconto racional composto, a taxa de juros ou desconto
racional (i) incide sobre o Valor Presente
(PV) a juros compostos. O Valor Presente
de um título com prazo n pode ser
calculado da seguinte forma:
Ex: Uma loja procurou um banco para
descontar uma nota promissória com
valor nominal de $ 65.000,00, com
vencimento em 8 meses. Determinar o
valor recebido pela loja e o desconto
aplicado, sabendo-se que o banco cobra
uma taxa de desconto racional composto
de 3% a.m.
Solução:
FV = 65.000,00
n = 8 meses
i = 3% a.m.
PV = ?
D = FV – PV
D = FV -
PV = 51.311,60
]
D = FV x [ 1 -
D = FV x [
]
65.000,00 CHS
FV
0
PMT
3
i
8
n
PV
51.311, 60
Os cálculos do desconto racional composto
podem ser realizados facilmente através
das funções financeiras da HP-12C.
¾ Desconto
Bancário
PV
Valor presente
n
Tempo
i
Taxa de juros
FV
Valor futuro
PMT
Prestações
Prof. Gilberto de Castro Timotheo
Comercial
ou
A maior parte das operações de
desconto comercial ou bancário (desconto
"por fora") é calculada no regime de juros
simples. No entanto, em algumas situações, pode ser utilizado o mecanismo de
Página 20
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
desconto comercial ou bancário (desconto
"por fora") a juros compostos.
No desconto "por fora" composto, a
taxa de desconto (d) incide sobre o Valor
Futuro (FV) a juros compostos. O Valor
Presente (PV) de um título com prazo n
pode ser calculado da seguinte forma:
A taxa de juros (i) compostos
implícita na operação é superior à taxa de
desconto (d) composto de 3% a.m.
FV = PV x
65.000,00 =50.943,32x
(1 + i)8
i = 3,09% a.m.
D = FV – PV
D = FV -
50.943,32
PV
65.000,00 CHS
FV
0
PMT
8
n
i
3,09
D = FV x [1 -
Ex: Uma loja procurou um banco para
descontar uma nota promissória com
valor nominal de $ 65.000,00, com
vencimento em 8 meses. Determinar o
valor recebido pela loja e o desconto
aplicado, sabendo-se que o banco cobra
uma taxa de desconto comercial
composto de 3% a.m. Qual é a taxa
mensal de juros compostos na operação?
Solução:
FV = 65.000,00
n = 8 meses
d = 3% a.m.
PV = ?
i=?
Conforme demonstra a
tabela comparativa abaixo
resume os
exemplos
anterios dês te tópico de
operações com desconto
considerando uma taxa
nominal de 3%
Desconto Racional 12.580,65 52.419,35
Simples
2,73%
a.m.
Desconto
15.600,00 49.400,00 3,49%
Comercial Simples
a.m.
Desconto Racional 13.688,40 51.311,60
Composto
3,00%
a.m.
Desconto
Comercial
Composto
3,09%
a.m.
14.056,68 50.943,32
PV = FV x
PV= 65.000,00 x (1 - 3%)8
PV= 50.943,32
Prof. Gilberto de Castro Timotheo
Página 21
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Exercícios Propostos
5.
1. Uma loja procurou um banco para
descontar uma nota promissória com
valor nominal de $ 100.000,00, com
vencimento em 6 meses. Determinar
o valor recebido pela loja e o desconto,
sabendo-se que:
Uma empresa ãefactoríng compra
cheques pré-datados de 3 meses por
80% do valor nominal. Determinar a
taxa mensal de desconto comercial
simples e a taxa mensal de juros
compostos do financiamento.
6.
Uma loja procurou um banco para
descontar uma letra de câmbio de $
85.000,00, com prazo de 134 dias. O
banco exige a retenção de 10% do
valor nominal a título de saldo médio,
permanecendo este valor bloqueado e
sem remuneração na conta da loja até
a data de vencimento da letra de
câmbio. Caso a loja realize a operação
de desconto, poderá sacar hoje um valor
líquido de $ 50.000,00. Assumindo o
ano comercial, determinar a taxa
anual de desconto comercial simples
e a taxa mensal de juros compostos
da operação.
¾
a) o banco cobra uma taxa de
desconto racional simples de 2% a.m.;
b) o banco cobra uma taxa de
desconto comercial simples de 2%
a.m.;
c) o banco cobra uma taxa de
desconto racional composto de 2%
a.m.;
d) o banco cobra uma taxa de
desconto comercial composto de 2%
a.m.
2.
Determinar o valor antecipado e a
taxa mensal de juros compostos
implícita no desconto de um cheque
pré-datado de $ 5.000,00, 6 meses
antes do vencimento, a uma taxa de
desconto comercial simples de 3%
a.m.
3. Uma letra de câmbio de $ 5.000,00 foi
descontada, resultando na antecipação
de $ 4.200,00 hoje. Determinar o
vencimento do título e a taxa mensal
de juros compostos, sabendo-se que a
taxa de desconto comercial simples é
de 4% a.m.
4.
Uma nota promissória de $ 4.000,00,
com prazo de 32 dias, foi descontada a
uma taxa de desconto comercial
simples de 23% a.a. Assumindo o ano
comercial, determinar o valor
antecipado e a taxa mensal de juros
compostos implícita na operação.
Prof. Gilberto de Castro Timotheo
7. Determinar a taxa anual de desconto
comercial simples em uma operação
de desconto de um título de 98 dias,
onde o valor antecipado é de 82% do
valor nominal. Obs.: assumir ano
civil.
8.
Uma empresa tem três notas
promissórias com valor nominal de $
15.000,00 e vencimentos em 5, 8 e 10
meses. Determinar o valor recebido
pela loja, sabendo-se que o banco cobra
uma taxa de desconto comercial
simples de 3% a.m.
9.
Uma loja desconta um cheque prédatado de $ 3.000,00, com vencimento
em dois meses, a uma taxa de
desconto comercial simples de 3,5%
a.m. O banco exige ainda um saldo
médio de 20% do valor nominal, a ser
retido
durante
o
prazo
do
financiamento,
o
qual
será
remunerado a uma taxa de juros
compostos de 1% a.m. Determinar a
taxa mensal de juros compostos do
Página 22
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
financiamento, sem e com a retenção
do saldo médio.
10. Determinar a taxa mensal de juros
compostos do financiamento do exercício
anterior, supondo que o banco exige,
além do saldo médio, 3% do valor nominal como despesa administrativa da
operaçao.
¾ Gabarito
1.
a) $ 10.714,29 e $ 89.285,71
b) $ 12.000,00 e $ 88.000,00
c) $ 11.202,86 e $ 88.797,14
d) $ 11.415,76 e $ 88.584,24
2.
$ 4.100,00 e 3,36% a.m.
3. 4 meses e 4,46% a.m.
4.
$ 3.918,22 e 1,96% a.m.
5. 6,67% a.m. e 7,72% a.m.
6.
83,76% a.a. e 9,99% a.m.
7. 67,04% a.a.
8.
$ 34.650,00
9. 3,70% a.m. e 4,42% a.m.
10. 6,64% a.m.
Prof. Gilberto de Castro Timotheo
Página 23
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Anuidade Postecipada
Fluxo de Caixa Uniforme
PMT
¾ Conceito de Anuidade ou
Série
Silva define como anuidade ou série um
conjunto
de
prestações
positivas(recebimentos, entradaas de
caixa) ou negativas ( pagamentos, saídas
de caixa), períodicas e constantes,
podendo ser finitas(quando ocorrem
dentro de um período determinado de
tempo) ou infinita(quando ocorrem para
sempre,
também
chamadas
perpetuidades).
0
n
PV
Anuidade Antecipada
PMT
0
n-1 n
PV
Anuidade Finita
Anuidade diferida
PMT
PMT
0
0
1
2
3
n
n
PV
PV
Anuidade Infinita
PMT
.......
0
......
PV
Prof. Gilberto de Castro Timotheo
¾
Séries Uniformes
Equivalentes
Dada uma série não uniforme de
pagamentos ou recebimentos, pode-se
transformá-la em uma série uniforme
equivalente (SUE), com a utilização de
calculadora financeira.
Página 24
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
¾ Transformação de um valor
em SUE (Série Uniforme
Equivalente)
Suponha-se que um valor presente
de $ 60.000 deva ser transformado em
uma SUE, conhecendo-se a taxa de juros
e o número de capitalização.
Na calculadora financeira:
VP
=-$60.000,00
i
= 15% a.p. (ao período)
N
=4
PMT = ?
A SUE (teclaPMT) desse fluxo de caixa é
de $ 21.015,92.
¾ Transformação de
desembolso de diversas data
em SUE.
Agora, suponha-se que a seguinte
distribuição de valores (não confundir o
gráfico a seguir com o fluxo de caixa) deva
ser transformada em uma SUE, com
desembolso a partir do período l,
mantendo-se a taxa de juros de 15% a.p.
Essa distribuição de valores poderia ser
representada da seguinte forma:
0
1
2
3
4
40000 14000 14000 14000 14000
3498,12
----------.
48980,12
Uma vez que já se conhece uma parte
da SUE ($14000), basta calcular as
SUEs dos seguintes valores e adicionálas à parte já conhecida.
0
4
40000
34980,12
Desembolso do período 0:
VP =-$40.000,00
i = 15%a.p.
N =4
PMT = ?
PMT = $ 14.010,61
Desembolso do período 4:
VF = - $ 34.980,12
0
1
2
3
4
i = 15%a.p.
N- = 4
40000 14000 14000 14000 48980,12
PMT = ?
PMT = $ 7.005,31
Prof. Gilberto de Castro Timotheo
Página 25
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Um empresário adquiriu equipamentos,
com valor de $ 36.000,00, a ser pago em 36
prestações mensais e iguais, com uma
taxa de juros de 1,8% a.m. Determinar o
valor das prestações, caso a primeira
parcela seja paga: (a) l mês após a
compra; (b) a vista.
Assim, temos:
SUE = $ 14.000,00 + $ 14.010,61 + $
7.005,31 = $ 35.015,92
Outra maneira de se calcular a SUE é
se obter a soma dos valores presentes
na data “0” das anuidades e então
utilizar este valor como Pv aplicando na
formula de PMT.
Solução:
PV = 36.000,00
FV = 0,00
n = 36 meses
9 Fórmulas das Anuidades
i = 1,8% a.m.
PMT = ?
FV = PMT x
A ) Série Postecipada
PV = FV x
PMT = PV x
Para as prestações infinitas e
postecipadas, teremos uma perpetuidade.
Nestes casos, quando n tende ao infinito, as
equações para determinar o PV e o PMT
tendem para:
PV =
[g]
END
36.000,00
PV
1,8
i
0
FV
36
n
PMT
- 1.367,42
PMT = PV x i
B) Série Antecipada
Ex:
Prof. Gilberto de Castro Timotheo
Página 26
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
BEG
36.000,00
PV
1,8
I
0
FV
36
N
PMT
- 1.367,42
9
Exercícios Propostos
9
1. Uma loja contraiu um financiamento
de $ 6.000,00, a ser pago em 8 prestações mensais e iguais de $ 1.000,00.
Determinar a taxa mensal de juros
do empréstimo, caso a primeira
parcela seja paga: (a) l mês após a
liberação dos recursos; (b) a vista.
2.
Um
empresário
adquiriu
equipamentos com valor de $
48.000,00, a ser pago em 48
prestações mensais e iguais, com uma
taxa de juros de 0,8% a.m. Determinar o valor das prestações, caso
a primeira parcela seja paga: (a) l
mês após a compra; (b) a vista.
3. 3.
Um investidor adquiriu um título
que rende 10 prestações trimestrais
iguais de $ 3.000,00, com a primeira
vencendo l trimestre após a compra.
Determinar o valor do investimento
realizado, sabendo que a taxa de juros
é de 2% a.t.
4. 4. Um pai, interessado em fazer uma
poupança para seu filho, resolveu
depositar mensalmente $ 500,00,
durante 21 anos, com o primeiro
depósito sendo efetuado daqui a um
mês.
Determinar
o
montante
disponível para o filho, ao final do
Prof. Gilberto de Castro Timotheo
período, sabendo que a taxa de juros
é de 0,5% a.m.
5. 5.
Determinar o valor de emissão de
um título de renda fixa com valor de
resgate de $ 1.000,00 e rendas anuais
postecipadas de $ 80,00 até seu
vencimento em 3 anos, sabendo que
a taxa de juros é de 6% a.a.
6. 6.
Um DVD é vendido em 6
prestações de $ 200,00, a serem
pagas ao final de cada bimestre após
a compra. Sendo a taxa de juros de
1% a.m., determinar o valor do
aparelho a vista.
7. 7.
Uma loja, realizando promoções
de Natal, vende uma geladeira por $
l.000,00, em 5 parcelas mensais "sem
juros" de $ 200,00, vencendo a
primeira 30 dias após a compra.
Determinar a taxa mensal de juros
implícita na operação, sabendo que a
loja oferece um desconto de 10%
para pagamento a vista.
8. 8.
Um lojista financiou a compra de
uma máquina de $ 30.000,00,
propondo-se a pagar 12 prestações
mensais iguais, sendo a primeira
parcela no final de 6 meses após a
compra. Determinar o valor das
prestações mensais, sabendo-se que a
taxa de juros é de 2% a.m.
9. 9.
Um empresário tomou um
financiamento de $ 75.000,00, para
ser pago em 15 prestações mensais,
iguais e postecipadas a uma taxa de
1% a.m. Imediatamente após o nono
pagamento, o empresário propôs
uma renegociação ao banco, que
aceitou refinanciar em 12 prestações
mensais adicionais, todas do mesmo
valor, a serem pagas a partir do final
do décimo mês. Determinar o valor
das novas prestações mensais,
sabendo que a taxa de juros da
operação permanece a mesma.
Página 27
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
10. 10. Um operário realizou 4 depósitos
iguais e sucessivos, no final de
janeiro, fevereiro, março e abril. No
final de julho, o total acumulado era
de $ 5.000,00. Determinar o valor dos
depósitos efetuados, sabendo-se que o
banco lhe ofereceu uma taxa de juros
de 2,5% a.m.
9 Gabarito
1.
6,88% a.m. e 9,20% a.m.
2.
$ 1.208,20 e $ 1.198,62
3.
$ 26.947,76
4.
$ 251.437,06
5.
$ 1.053,46
Um fluxo de caixa irregular (não
uniforme) consiste em uma sequência de
entradas e saídas de caixa de
intensidades, sinais e periodicidades
diferentes. Em um fluxo de caixa
irregular, não conseguimos trabalhar
direta e facilmente com as cinco funções
financeiras básicas (PV, FV, PMT, i e n).
A Figura 7.1 mostra a configuração de
um fluxo de caixa irregular.
Para analisarmos estes fluxos o faremos
através do Valor Presente Líquido ( VPL
ou na HP – NPV) e a Taxa interna de
Retorno (TIR ou na HP - IRR ).
9 Valor Presente Líquido
6. $ 1.119,91
7. 3,62% a.m.
8.
$ 3.132,04
9.
$ 2.785,35
10. $ 1.118,12
O valor presente líquido (VPL) ou net
present value (NPV) é igual ao valor
presente de todas as entradas e saídas
futuras de caixa. Para um fluxo de
entradas e saídas de caixa desiguais ao
longo de um horizonte de tempo n, o valor
presente líquido pode ser calculado
através da fórmula:
VPL =
+
+
+
+.....+
Onde:
Fluxo de Caixa Irregular
9 Conceito
Prof. Gilberto de Castro Timotheo
FCo = Fluxo de caixa inicial
FCn = Fluxo de caixa no período n
Página 28
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
i = Taxa de juros
n = Prazo
Quando o valor presente líquido é
positivo, isso significa que os fluxos futuros de caixa trazidos e somados a valor
presente superam o investimento inicial.
Portanto, o fluxo de caixa agrega valor e
é atrativo do ponto de vista econômi-cofinanceiro.
Por outro lado, quando o valor
presente líquido é negativo, os fluxos
futuros de caixa trazidos e somados a
valor presente são inferiores ao
investimento inicial. Logo, o fluxo de
caixa destrói valor e não deveria ser
realizado.
Quando o valor presente líquido é
zero, os fluxos futuros de caixa trazidos e
somados a valor presente são exatamente
iguais ao investimento inicial. Nesta situação, ficamos em uma posição de
indiferença para realizar ou não o
investimento.
9
Quando o valor presente líquido é negativo,
o projeto destrói valor, pois o investimento está
sendo remunerado a uma taxa de retorno (TIR)
inferior à taxa desejada (i).
Quando o valor presente líquido é zero,
ficamos em uma posição de indiferença para
fazer ou não o projeto, pois o investimento está
sendo remunerado a uma taxa de retorno (TIR)
igual à taxa desejada (i).
VPL
TIR
Decisão
>0
>i
Fazer
=0
=i
indiferente
<0
<i
Não fazer
9 Teclas utlizadas para as
operações de fluxo de
caixa
Taxa Interna de Retorno
A taxa interna de retorno (TIR) ou
internal rate of return (IRR) mede a rentabilidade do fluxo de caixa. O cálculo da
TIR não é direto, uma vez que não existe
uma fórmula específica. Na verdade, a
TIR é a taxa de juros (i) que iguala o VPL
de um fluxo de caixa a zero.
Quando o valor presente líquido é positivo,
isso significa que o projeto agrega valor, ou
seja, o investimento está sendo remunerado a
uma taxa de retorno (TIR) superior à taxa
desejada (i).
Prof. Gilberto de Castro Timotheo
[f]NPV Valor presente líquido
[f] IRR
Taxa interna de retorno
tg] CF0 Fluxo de caixa no tempo 0
[g] CF,
Fluxo de caixa no tempo j
[g] Nj
Número de parcelas CF, iguais e
Taxa detijuros
i
Página 29
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
As funções da HP-12C exigem que os
fluxos de caixa sejam informados de forma
sequencial nas funções [g] [CF,], à exceção
do fluxo de caixa no tempo O, que deve ser
informado na função [g] [CF0]. Deve-se
informar todas as parcelas, inclusive as
que tiverem valor nulo, além de observar
as convenções dos sinais, em que as
entradas de caixa devem ser inseridas
com valores positivos e as saídas de
caixa, com valores negativos. Antes de
começar qualquer exercício, é importante
limpar a memória da calculadora HP-12C
através da função [f] [REG].
Formato 2
O passo-a-passo para resolver esse
exercício na HP-12C pode ser visto a seguir. Quando existem fluxos de caixa
repetidos e seguidos, a calculadora HP12C permite economizar trabalho e
digitação, usando a tecla [g] N,. Como as
grandezas $ 400,00 e $ 500,00 se repetem
por 2 e 3 vezes, respectivamente,
podemos, alternativamente, usar a
função [g] Nj.
[f]
REG
1.200,00 CHS
[g] CF0
300,00
[g] CFj
400,00
[g] CFj
2
[g] Nj
500,00
[g] CFj
3
[g] Nj
20
i
[f] NPV
168,77
[f] IRR
25,02
Formato 1
[f]
REG
1.200,00 CHS
[g] CF0
300,00
[g] CFj
400,00
[g] CFj
400,00
[g] CFj
500,00
[g] CFj
500,00
[g] CFj
500,00
[g] CFj
20
i
[f] NPV
168,77
[f] IRR
25,02
Prof. Gilberto de Castro Timotheo
Página 30
CURSO DE MATEMÁTICA FINANCEIRA COM HP E EXCEL
Referências
Hoji, M. (2007). Administração Financeira e
Orçamentária. São Paulo: Editora Atlas S.A.
Santos, E. O. (2001). Administração
Financeira da Pequena e Média Empresa .
Sáo Pualo: editora Atlas S.A.
Silva, A. L. (2005). Matemática Financeira
Aplicada. São Paulo: Editora Atlas S.A.
Prof. Gilberto de Castro Timotheo
Página 31