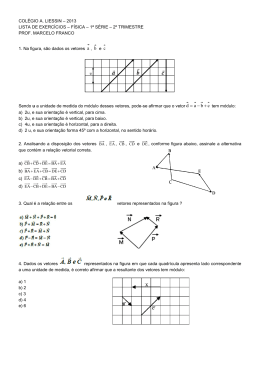
EB/S VIEIRA DE ARAÚJO – VIEIRA DO MINHO
Direção Regional de Educação
do Norte
Cód. 343389
Tel: 253647201
Fax: 253648245 [email protected]
Rua Dra. Maria Júlia Alves Martins 4850-549 Vieira do Minho
Teste de Avaliação N.º2 – MATEMÁTICA A – 11.º Ano
Duração: 90 minutos
Nome:___________________________________________________________
Enc. Educação: ___________________________
Nº ____ Turma: C_
A Prof.: _______________
Data: _25_/ 11 / 2011
Classificação: ___________________
Grupo I
As questões deste grupo são de escolha múltipla.
Para cada uma delas, são indicadas quatro alternativas, das quais apenas uma está correta.
Escolhe a opção e escreve-a na tua folha de teste.
Atenção: se apresentares mais do que uma resposta, a questão será anulada, o mesmo acontecendo em
caso de resposta ambígua.
1. Na figura estão representados um referencial o.m. xOy, o círculo
trigonométrico e um triângulo retângulo [OAB].
3
da medida do
2
A medida do comprimento do segmento de reta [AB] é
comprimento do raio.
Qual é, aproximadamente, a amplitude do ângulo β representado na figura?
(A) −121º
(B) −123º
(C) −124º
(D) −140º
2. Se tg 2 x = 1 , então pode concluir-se que:
(A) x =
(C) x =
π
4
+ kπ , k ∈ ℤ
(B) x =
kπ
, k ∈ℤ
2
π
4
(D) x = −
+
π
4
kπ
, k ∈ℤ
2
+ kπ , k ∈ ℤ
3. Sejam u e v vetores não nulos tais que u . v = 2 || u ||2 e || v ||= 2 || u || .
Qual das seguintes afirmações é verdadeira?
(A) A amplitude do ângulo formado pelos vetores u e v é π .
(B) O comprimento do vetor u é o dobro do comprimento do vetor v e os dois vetores têm o mesmo
sentido.
(C) Os vetores u e v são colineares e têm o mesmo sentido.
(D) Os vetores u e v são perpendiculares.
Teste de Avaliação Nº 2 – Matemática A - 11º ano
2011/2012
1/4
π

cos  + x  − sen (π + x )
2

4. No respetivo domínio, a expressão
é equivalente a:
3π 

2 cos  x +

2 

(A) tg x
5.
(C) −1
(B) 0
(D) 1
Na figura estão representados o círculo trigonométrico e dois
vetores, OA e OB , ambos de norma 2.
P é o ponto de interseção do segmento de reta [OA] com a
circunferência e tem abcissa −
1
.
2
Q é o ponto de interseção do segmento de reta [OB] com a
circunferência e tem abcissa
3
.
2
Os pontos P e Q pertencem à circunferência.
Qual é o valor do produto escalar OA . OB ?
(A) −2 3
(B) −4 3
(C) -2
(D) -4
Grupo II
Nos itens deste grupo apresenta o teu raciocínio de forma clara, indicando todos os cálculos que tiveres de
efetuar e todas as justificações necessárias.
Quando, para um resultado, não é pedida a aproximação, pretende-se sempre o valor exato.
1.
Considera a função f, real de variável real, definida no intervalo
[0,10] , por:
π
π
f ( x) = 20 − 5sen  x −  ,
2
4
cujo gráfico está representado ao lado.
Os pontos A, B e C pertencem ao gráfico de f e são extremos da função.
Determina analiticamente:
2.
1.1.
o valor exato de f (5) .
1.2.
o contradomínio de f.
1.3.
as coordenadas dos pontos A, B e C.
Resolve, em ℝ , a equação:
2sen ( 3x ) − sen ( 3x ) .cos(π − x) = 0
Teste de Avaliação Nº 2 – Matemática A - 11º ano
2011/2012
2/4
3.
B
Na figura está representada uma circunferência de centro O e raio
C
[OC], em que OC = 6 cm .
30º
Determina:
4.
3.1.
OC . OA
3.2.
BA . BO
A
O
Considera os pontos A ( −2,1, 3) e B ( 0, −5, 2 ) e os vetores u , v e w tais que u = ( −1, 2, 4 ) ,
|| w ||= 2 , u . w = −3 e v = ( 4, 1 − 3a, 1) .
4.1. Determina, com aproximação às décimas de grau, a amplitude do ângulo formado pelos vetores
u e w.
4.2.
(
)
Calcula u . AB − 2 w .
4.3. Determina os valores de a de modo que os vetores v e u sejam perpendiculares.
5.
Na figura está representado um relógio de uma estação de caminho de ferro.
O mostrador é um círculo e está apoiado numa barra.
Sabe-se que t minutos após as zero horas,
• a distância (em metros), da extremidade do ponteiro das horas à barra, é dada por
 πt 
h(t ) = 1 + 0.5cos 

 360 
• a distância (em metros), da extremidade do ponteiro dos minutos à barra, é dada por
πt 
m(t ) = 1 + 0.7 cos  
 30 
Nota: tanto em h como em m, o argumento da função cosseno está expresso em radianos.
Teste de Avaliação Nº 2 – Matemática A - 11º ano
2011/2012
3/4
5.1. Determina a distância da extremidade do ponteiro dos minutos à barra às 1h 35min. Apresenta
o resultado em centímetros, com aproximação às unidades. Em cálculos intermédios conserva,
no mínimo, 3 casas decimais.
5.2. Seja A a extremidade do ponteiro das horas e seja B a
extremidade do ponteiro dos minutos.
Tal como a figura junta ilustra, passado pouco tempo
das zero horas, a reta AB é paralela à barra na qual o
relógio está apoiado.
Pouco antes da 1 hora (da manhã), há outro instante em
que isso acontece.
Equaciona o problema e recorrendo às potencialidades
da calculadora gráfica, determina esse instante,
apresentando o resultado em horas, minutos e segundos (segundos arredondados às unidades).
Apresenta todos os elementos recolhidos na calculadora, nomeadamente o gráfico ou gráficos
obtidos e coordenadas de pontos relevantes, com aproximação às milésimas.
FIM
Bom trabalho!
A professora
Questão
Grupo I
Cotação
10 x 5 = 50
Grupo II
1.1
1.2
1.3
2
3.1
3.2
4.1
4.2
4.3
5.1
5.2
5
8
20
15
10
15
14
14
10
9
30
Teste de Avaliação Nº 2 – Matemática A - 11º ano
2011/2012
TOTAL
200
4/4