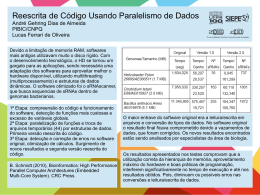
Mineração de Exceções
Apresentadores
Andrey C. Cavalcanti
George Soares da Silva
Introdução

Dados podem ser armazenados e resumidos em cubos
multidimensionais.(OLAP)

Um usuário ou analista pode usar operações OLAP
para encontrar padrões interessantes.

O processo de descoberta não é automático. Depende
da intuição ou hipóteses usadas pelo usuário.

Desvantagens da exploração baseada em hipóteses:

espaço de busca muito grande

agregações de alto nível não indicam anomalias

dificuldade mesmo se o espaço for pequeno
24/5/2001 12:00
Análise de Outliers
Outliers  Exceções
 Causa dos Outliers → erro de execução ou
medida.


Exemplo: Inserção default de um valor
Falsos Outliers (Ex: salários de executivos)
 Mineração de outliers → consiste na
detecção e análise de outliers (complexo e
interessante)

24/5/2001 12:00
Aplicações de Mineração de Outliers
1.
Detecção de Fraudes ( cartões de crédito
ou telefone)
2.
Comportamento de gastos de consumidores
( por classe social )
3.
Em análises médicas ( resultados não
esperados de tratamentos )
24/5/2001 12:00
Mineração de Outliers

Pode ser dividido em 2
subproblemas:
1.
2.
3.
Definir quais dados
são aberrantes
Definir método
eficiente para
encontrar tais
aberrações
Aberrante sempre
com referência a
algum padrão
24/5/2001 12:00

Métodos de detecção:
Semi-automático:
 Visualização
 Automático
 Estatística
 Distância
 Desvio
Observação:
 Usuário tem que
checar se os outliers
descobertos são
realmente outliers.


Detecção de Outliers baseada em
Estatística




Distribuição ou modelo probabilístico ( Ex:
distribuição normal )
Teste de discordância (TD)→ identifica os
outliers com respeito ao modelo escolhido
O TD examina 2 hipóteses:
 de trabalho
 alternativa
Um dado ser ou não ser Outlier depende da
distribuição escolhida
24/5/2001 12:00
Detecção de Outliers baseada em
Estatística

2 procedimentos para
detecção de outliers:
 Procedimentos em
blocos
 Procedimentos
consecutivos
(sequencial)
 menos provável é
testado
 mais eficiente
24/5/2001 12:00

Conclusão

Testa aberração ao
longo de apenas uma
única dimensão

Dificuldade na
escolha de uma
distribuição padrão,
especialmente com
dados desconhecidos
Um exemplo de detecção de Outliers
baseado em estatística






O Procedimento abaixo é feito para cada observação xi,onde
i=1..n e k = n-1:
vetor médio da amostra
 xm = (1/k) Σxi (p/ i de 1 à k)
Matriz de covariância
 S = (1/(k-1)) Σ(xi – xm) (xi – xm)’
Distância de Mahalanobis:
2
-1
 D = (x – xm)’S (x – xm)
Distribuição F com p e k-p graus de liberdade
 F = ((k – p)k / (k2 – 1)p) D2
A partir de F calcula-se o valor de P que será comparado com
o nível de significância ά
 Se P < ά, então encontramos um outlier, remove o mesmo e
refaz o procedimento acima
 Se P > ά, está OK
24/5/2001 12:00
Exemplo de Detecção de Outliers
baseada em Estatística
Observ
1
2
3
4
5
6
7
8
9
X1:Sist
154
136
191
125
133
125
93
80
X2:Dias
108
90
54
89
93
77
43
50







10 11
12
13
14
15
132
10
7
142
115
114
120
141
125
76
96
74
79
71
90
Nível de significância ά=0,05
Primeiro encontrou as médias e os desvio padrões iguais à:
 x1 = 120,6 e s1 = 20,9
 x2 = 81,0 e s2 = 21,7
Com n=15, removemos x9 por ter tido o menor valor de
P=0,0003
Agora temos n=14 e remove x7 com P=0,0264
Agora temos n=13 e não há mais outliers detectados.
Neste momento, temos as seguintes médias e desvios:
 x1 = 121,8 e s1 = 20,8 / x2 = 80,5 e s2 = 16,3
Valores corretos: x7=(93,54) e x9=(132,94)
24/5/2001 12:00
Detecção de Outliers baseada em
Distância

Origem → Resolver limitações do estatístico

O que é um outlier baseado em distância?
 um objeto ‘o’ num conjunto de dados ‘S’
 é um outlier baseado em distância DB(p,d),
 se pelo menos uma fração ‘p’ de objetos em ‘S’
 se encontram a uma distância maior que ‘d’ de ‘o’

Exemplo com pontos no plano
24/5/2001 12:00
Detecção de Outliers baseada em
Distância


Estatística X Distância
Conceito de distância ≠
Testes estatísticos
vantagens:
 evita suposição sobre
distribuição dos
dados
 custo computacional
menor
 em muitos casos:
 outlier baseado em
distância  outlier
estatístico
24/5/2001 12:00

Alguns algoritmos:




Index-based
Nested-loop
Cell-based
desvantagens
 Escolha dos
parâmetros ‘p’ e ‘d’.
Detecção de Outliers baseada em
Desvio


Nem estatística, nem distância
Outliers  Desvios

Identifica outliers a partir das características
do grupo

2 técnicas para detecção:
 Técnica de exceção sequencial
 Técnica de cubo de dados OLAP
24/5/2001 12:00
Técnica de Exceção Sequencial


Compara objetos sequencialmente num conjunto
(Exemplo: humanos na distinção de objetos)
Alguns termos chaves:
 Conjunto de Exceções


subconjunto mínimo de objetos cuja remoção
resulta na maior redução de dissimilaridade
Função de dissimilaridade


Ex: para dados numéricos variância
Ex: para dados categóricos diferença entre
proporções de objetos que se casam com padrão
simbólico com variáveis livres (aa**b)
24/5/2001 12:00
Técnica de Exceção Sequencial

Termos Chaves: (Cont.)
o
 Função de Cardinalidade → N de objetos
 Fator de suavização
 mede redução de dissimilaridade por
exclusão de subconjuntos, normalizado
pelo número de elementos
 Conjunto com maior fator de suavização =
Conjunto de exceções
24/5/2001 12:00
Técnica de Exceção Sequencial

Funcionamento da técnica

Pode a ordem dos subconjuntos na
sequência afetar o resultado ?
24/5/2001 12:00
Exploração Baseada em
Descoberta
Modelo usando o cubo de dados
 O especialista é vai procurar por anomalias
nos dados guiado por indicadores de
exceções pré-computados
 Modelo estatístico usado para computar o
valor esperado do dado
 Uso de ferramentas OLAP

24/5/2001 12:00
O Cubo de Dados
Dimensões
 Hierarquia
 Operações OLAP
 Drill down
 Roll up
 Slice

24/5/2001 12:00
Definindo Exceções em Cubos


Exceções são, intuitivamente, dados que nos
surpreendem
Como medir a ‘surpresa’?
 SelfExp
 Valor relativo ao seu próprio nível
 InExp
 Valor relativo ao drill-down em todos as
dimensões
 PathExp
 Um InExp relativo a um determinada dimensão
24/5/2001 12:00
Exemplo
24/5/2001 12:00
Exemplo
24/5/2001 12:00
Exemplo
24/5/2001 12:00
Exemplo
24/5/2001 12:00
Exceções em Cubos: a qual
granularidade?
Quanto menor a granularidade, mais fácil
será achar uma(s) exceção(ões)
 Uma exceção pode ser considerada uma
exceção por um group-by e não ser
considerada por outro group-by
 Exemplo

24/5/2001 12:00
Cálculo do Valor Esperado
O valor esperado é calculado levando em
conta a contribuição dos vários níveis de
group-by
 Exemplo:

ŷijk = f(γ, γiA, γjB, γkC, γijAB, γjkBC, γikAC)
 yijk é uma exceção se:
 (yijk – ŷijk)/ ijk > ( = 2.5)
 Por que o valor de  é 2.5?
 Qual o valor de ijk?

24/5/2001 12:00
Cálculo do Valor Esperado

A função f() pode ser das seguintes formas:
 Aditiva

n
f   i
i 0

Multiplicativa
n

f   i
i 0

Outras mais complexas
24/5/2001 12:00
Cálculo do Valor Esperado

O valor de ŷijk é:


(γ + γiA + γjB + γkC + γijAB + γjkBC + γikAC)
ŷijk = e
Para o caso de um cubo com 3 dimensões, usando
a forma aditiva de f()
24/5/2001 12:00
Cálculo do Valor de cada γ
Primeiro calcula o nível específico
 γ = l+...+
 Para cada dimensão, suba um nível , calcule
o valor de γ como sendo:
 γirAr = l+...+ir+...+ - γ
 Para os níveis acima, faça o mesmo, da
forma
 γirisArAs = l+...+ir+...+ is+...+ - γirAr - γisAs - γ

24/5/2001 12:00
Exemplificando
A
B
C
A,B
A,C
B,C
A,B,C
24/5/2001 12:00
Cálculo do valor de ijk
A fórmula de ijk é:
2

  ijk = (ŷijk)
 onde tem que satisfazer a equação (baseada
no princípio da máxima verossimilhança):

(yijk - ŷijk)2
log ŷijk  log ŷijk
0

(ŷijk)

24/5/2001 12:00
Estimando os Coeficientes do
Modelo (γ)



Baseada na média
 Ex: Formar uma linha de regressão e remover
da consideração 10% dos pontos que se
encontram mais longe da mesma
Baseada em média “emagrecida”
Baseada na mediana
 Mais robusta, pois é melhor na presença de
outliers muito grandes
 Alto custo computacional → muitas vezes
impraticável
24/5/2001 12:00
Exemplo
24/5/2001 12:00
Outros Tipos de Modelo
Hierárquico
 A idéia é calcular o valor esperado
baseado na sua posíção e parentes na
hierarquia
 Série de Regressão Temporal
 Baseado na idéia que as células tem um
atributo temporal
 É possível encontrar padrões em períodos

24/5/2001 12:00
Outros métodos
Valor extremo no conjunto
 Clustering
 Clustering multi-dimensional
 Regressão em dimensões contínuas
 Efeitos combinados de dimensões
categóricas

24/5/2001 12:00
Referências



Data Mining: concepts and techniques, de Han, J. &
Kamber, M., 2001, Morgan Kaufmann
Data Mining: practical machine learning tools and
techniques with Java implementations, de Witten, I.H. &
Frank, E., 2000, Morgan Kaufmann
Discovery-driven Exploration of OLAP Data Cubes, de
Sunita Sarawagi, Rakesh Agrawal, Nimrod Megiddo,
IBM Research Division
24/5/2001 12:00