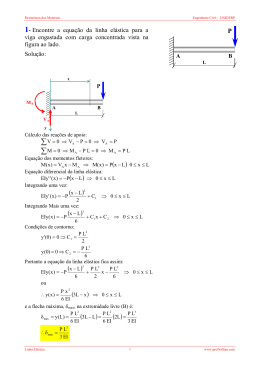
12.30 O eixo suporta as cargas das três polias mostradas. Determinar a deflexão em
seu centro e sua inclinação em A e B. Os mancais exercem apenas reações verticais
sobre ele e EI é constante.
Solução:
Reações de apoio:
3P
3P
VA =
VB =
2
2
As equações de momento fletor são:
M 1 ( x ) = −Px ⇒ 0 ≤ x ≤ a
3P
( x − a ) ⇒ a ≤ x ≤ 2a
2
3P
M 3 ( x ) = − Px +
( x − a ) − P( x − 2a ) ⇒ 2a ≤ x ≤ 3a
2
3P
3P
( x − 3a ) ⇒ 3a ≤ x ≤ 4a
M 4 ( x ) = −Px +
( x − a ) − P ( x − 2a ) +
2
2
Agora, vamos montar as equações diferenciais da linha elástica (uma para cada trecho):
EIy1 ' ' ( x ) = Px ⇒ 0 ≤ x ≤ a
M 2 ( x ) = −Px +
3P
( x − a ) ⇒ a ≤ x ≤ 2a
2
3P
EIy 3 ' ' ( x ) = Px −
( x − a ) + P( x − 2a ) ⇒ 2a ≤ x ≤ 3a
2
3P
3P
EIy 4 ' ' ( x ) = Px −
( x − a ) + P ( x − 2a ) −
( x − 3a ) ⇒ 3a ≤ x ≤ 4a
2
2
E, assim, resolvê-las através de duas integrações. Primeira integração:
x2
EIy1 ' ( x ) = P
+ C1 ⇒ 0 ≤ x ≤ a
2
x 2 3P ( x − a ) 2
EIy 2 ' ( x ) = P
−
+ C 2 ⇒ a ≤ x ≤ 2a
2
2
2
x 2 3P ( x − a ) 2
( x − 2a ) 2
EIy 3 ' ( x ) = P
−
+P
+ C 3 ⇒ 2a ≤ x ≤ 3a
2
2
2
2
x 2 3P ( x − a ) 2
( x − 2a ) 2 3P ( x − 3a ) 2
EIy 4 ' ( x ) = P
−
+P
−
+ C 4 ⇒ 3a ≤ x ≤ 4a
2
2
2
2
2
2
EIy 2 ' ' ( x ) = Px −
Segunda integração:
x3
+ C1 x + C 5 ⇒ 0 ≤ x ≤ a
EIy1 ( x ) = P
6
x 3 3P ( x − a ) 3
−
+ C 2 x + C 6 ⇒ a ≤ x ≤ 2a
EIy 2 ( x ) = P
6
2
6
x 3 3P ( x − a ) 3
( x − 2a ) 3
−
+P
+ C 3 x + C 7 ⇒ 2a ≤ x ≤ 3a
EIy 3 ( x ) = P
6
2
6
6
x 3 3P ( x − a ) 3
( x − 2a ) 3 3P ( x − 3a ) 3
EIy 4 ( x ) = P
−
+P
−
+ C 4 x + C 8 ⇒ 3a ≤ x ≤ 4a
6
2
6
6
2
6
As condições de contorno para a viga são:
y'1 (a ) = y' 2 (a ) ⇒ C1 = C 2
y 1 ( a ) = y 2 (a ) ⇒ C 5 = C 6
y ' 2 ( 2a ) = y ' 3 ( 2a ) ⇒ C 2 = C 3
y 2 ( 2a ) = y 3 ( 2a ) ⇒ C 6 = C 7
y' 3 (3a ) = y' 4 (3a ) ⇒ C 3 = C 4
y 3 (3a ) = y 4 (3a ) ⇒ C 7 = C 8
a3
EIy1 (a ) = P + C1a + C 5 = 0
6
(3a ) 3 3P (3a − a ) 3
(3a − 2a ) 3
EIy 3 (3a ) = P
−
+P
+ C 3 3a + C 7 = 0
6
2
6
6
das duas últimas equações (fazendo C1=C3 e C5=C7) vem que:
5P
C1 = C 2 = C 3 = − a 2
4
13P 3
C 4 = C5 = C6 =
a
12
A deflexão no centro (centro, x=2a) é:
(2a ) 3 3P (2a − a ) 3 5Pa 2
13P 3
EIy 2 (2a ) = P
−
−
2a +
a
6
2
6
4
12
Pa 3
∴ y 2 ( 2a ) = y 2 a = −
3EI
As inclinações em A e B são:
a2
Pa 2 5Pa 2
3Pa 2
EI y1 ' (a ) = P + C1 =
−
=−
2
2
4
4
2
3Pa
∴ y 1 ' (a ) = θ A = −
4EI
2
(3a )
3P (3a − a ) 2
(3a − 2a ) 2 5Pa 2
EIy 3 ' (3a ) = P
−
+P
−
2
2
2
2
4
2
3Pa
∴ y 3 ' (3a ) = θ B =
4EI
Obs.: o eixo y positivo foi adotado para baixo.