B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
Utilize as informações a seguir para as questões 1 e 2.
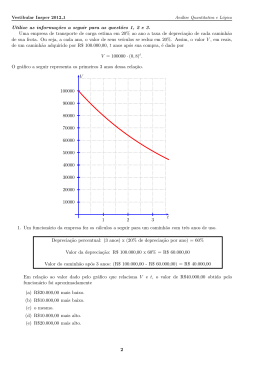
O gráfico a seguir representa a quantidade diária de pessoas (q) atendidas em um hospital público com os
sintomas de um novo tipo de gripe, a gripe X, em função do tempo (t), em meses, desde que se iniciou um
programa de vacinação para este tipo de gripe na cidade do hospital.
(número de atendidos por dia)
1200
1100
1000
900
800
700
600
500
400
300
200
100
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 t (meses)
1. A prefeitura da cidade fará uma campanha publicitária com frases que pretendem ressaltar os aspectos
positivos da vacinação. Das opções abaixo, aquela que informa corretamente o que o gráfico mostra
é
(a) “Em um ano de vacinação, a quantidade diária de atendimentos a pessoas com a gripe X caiu
de 1.000 para 10!”
(b) “A cada três meses, a quantidade de pessoas que chega todos os dias ao hospital com a gripe X
cai pela metade!”
(c) “O número de atendimentos diários no hospital a pessoas com a gripe X diminui em 400 a cada
4 meses!”
(d) “A cada mês, chegam ao hospital 100 pessoas a menos por dia, em relação ao mês anterior,
com os sintomas da gripe X.”
(e) “Entre o 3o e o 6o mês do programa de vacinação, 250 pessoas foram vacinadas contra a gripe
X diariamente no hospital.”
2. Das funções a seguir, aquela que melhor representa a relação proposta no gráfico é
1
(a) q(t) = 1000 · 2− 3 t .
(b) q(t) = 500 · 2−3t .
1
(c) q(t) = 1000 · 2 3 t .
(d) q(t) = 500 · log2 (3t).
1
t .
(e) q(t) = 1000 · log2
3
2
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
3. Para ilustrar a afirmação “Se beber, não dirija.” um designer criou a seguinte imagem:
8 .
Interprete as imagens a seguir, construı́das a partir do mesmo raciocı́nio utilizado pelo designer :
.
8
8 .
As afirmações que melhor representam essas imagens são, respectivamente,
(a) “Se dirigir, beba.” e “Se não dirigir, durma.”
(b) “Se não dirigir, beba.” e “Se dirigir, não durma.”
(c) “Se não dirigir, beba.” e “Se não dirigir, durma.”
(d) “Se dirigir, beba.” e “Se dirigir, não durma.”
(e) “Se não dirigir, beba.” e “Se dirigir, durma.”
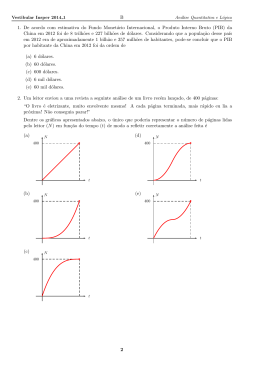
4. As quantidades de raı́zes reais dos polinônios p(x) = x4 + 10, q(x) = 10x2 + 1 e r(x) = p(x) − q(x)
são, respectivamente,
(a) 0, 0 e 4.
(b) 4, 0 e 4.
(c) 0, 2 e 2.
(d) 4, 2 e 2.
(e) 4, 2 e 4.
5. Uma pizzaria vende pizzas circulares com 32cm de diâmetro, divididas em 8 pedaços iguais. O dono
do estabelecimento pensou em criar uma pizza de tamanho maior, a ser dividida em 12 pedaços
iguais, de modo que a área de cada um deles seja igual à área de um pedaço da pizza menor. Para
isso, o diâmetro da pizza de 12 pedaços deve ser aproximadamente igual a
(a) 36cm.
(b) 40cm.
(c) 44cm.
(d) 48cm.
(e) 52cm.
3
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
6. As vendas de ingressos para um grande evento esportivo ocorreram durante dois meses. O gráfico a
seguir representa as vendas diárias, em milhares de unidades, durante este perı́odo.
50
40
30
20
10
0
0
5
10
15
20
25
30
35
40
45
50
55
Das opções a seguir, aquela que melhor representa o total (acumulado) de ingressos vendidos até cada
dia do perı́odo de vendas é
(Obs.: os gráficos das alternativas estão em uma escala diferente do gráfico acima.)
(a)
1000
800
600
400
200
0
0
5
10
15
20
25
30
35
40
45
50
55
0
5
10
15
20
25
30
35
40
45
50
55
0
5
10
15
20
25
30
35
40
45
50
55
0
5
10
15
20
25
30
35
40
45
50
55
0
5
10
15
20
25
30
35
40
45
50
55
(b)
1000
800
600
400
200
0
(c)
1000
800
600
400
200
0
(d)
1000
800
600
400
200
0
(e)
1000
800
600
400
200
0
4
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
Utilize as informações a seguir para as questões 7 e 8.
Sejam A e B matrizes com todos os elementos reais, sendo A quadrada de ordem 3 e B uma matriz
coluna com 3 linhas. Sabe-se que:
• A é uma matriz triangular superior, ou seja, todos os elementos abaixo de sua diagonal principal
são nulos;
• Todos os elementos que não estão abaixo da diagonal principal de A são iguais a 1;
• B = (bi ), com bi = 4 − i, para todo i ∈ {1, 2, 3}.
Considere, também, que I3 denota a matriz identidade de ordem 3.
7. Sabendo que o traço de uma matriz quadrada é a soma dos elementos de sua diagonal principal, o
traço da matriz (A + 3 · I3 ) é
(a) 3.
(b) 4.
(c) 6.
(d) 12.
(e) 16.
8. Seja X uma matriz coluna de 3 linhas tal que AX = B. Então, a soma dos elementos de X é igual a
(a) 2.
(b) 3.
(c) 4.
(d) 6.
(e) 10.
9. Seja z ∈ C um complexo de módulo |z| e argumento θ, θ ∈] − π, π]. Defina w ∈ C da seguinte forma:
w = log3 |z| + i · θ
Se w = 2 + i · π2 , o valor de z 10 é
(a) 910 .
(b) −910 .
(c) 910 · i.
(d) −910 · i.
(e) 1.
5
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
Utilize as informações a seguir para as questões 10 e 11.
Considere uma esfera de raio medindo R e um plano que a tangencia. Pode-se associar a ela um
outro sólido, obtido da seguinte maneira:
• constrói-se um cilindro equilátero de raio R com uma das bases contida no plano;
• retira-se desse cilindro dois cones circulares, sendo que a base de cada um deles coincide com
uma das bases do cilindro e os vértices coicidem em V , no centro desse cilindro.
O sólido que resta após a retirada dos cones é chamado de anticlepsidra e tem o mesmo volume da
esfera. Ambos os sólidos estão representados na figura abaixo.
10. Apesar de terem o mesmo volume, a esfera e a anticlepsidra associada não têm a mesma área superficial. A razão entre a área da superfı́cie esférica e a área da superfı́cie da anticlepsidra é
(a) 2
√
2−1 .
(b) 2.
√
(c) 2 2.
√
(d) 2 − 2.
√
(e) 2 + 1.
11. Uma anticlepsidra tem volume igual a π. O raio da esfera associada tem medida
(a)
(b)
(c)
(d)
(e)
√
3
12
4 .
√
3
6
2 .
q
3
4
3.
√
3
2 .
√
3
4 .
6
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
12. O gráfico da função f : R → R, dada por f (x) = x2 − 5|x| + 6, é melhor representado por
(d)
(a)
y
6
5
5
4
4
3
3
2
2
1
1
−5 −4 −3 −2 −1
−1
(b)
y
6
1
2
3
4
x
−5 −4 −3 −2 −1
−1
−2
(e)
y
1
2
3
4
−2
y
6
1
5
−5 −4 −3 −2 −1
−1
4
3
−2
2
−3
1
−4
−5 −4 −3 −2 −1
−1
(c)
1
2
3
4
−5
x
−6
−2
−7
y
6
5
4
3
2
1
−5 −4 −3 −2 −1
−1
1
2
3
4
x
−2
7
1
2
3
4
x
x
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
13. A função g, de domı́nio real, tem parte de seu gráfico mostrada na figura a seguir.
y
2
1
−3
−2
−1
−1
1
2
x
O gráfico da função f (x) = x · g(x) é melhor representado por
(a)
(d)
y
y
2
1
−3
−2
1
−1
−1
1
2
x
−3
−2
−1
−1
1
2
x
1
2
x
−2
(b)
(e)
y
y
1
−3
−2
1
−1
−1
1
2
x
−3
−2
y
2
1
−2
−1
−1
−1
−1
−2
(c)
−3
−2
1
2
x
8
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
Utilize as informações a seguir para as questões 14 e 15.
É fato conhecido por estudantes do ensino médio que uma circunferência de raio medindo R tem
comprimento igual a 2πR. Porém, nem sempre a humanidade soube calcular tal comprimento, e para
isso lançou mão de aproximações. Um dos jeitos de se estimar o comprimento da circunferência é
inscrevendo-se nela um polı́gono regular; quanto mais lados tiver o polı́gono, melhor a aproximação.
A figura a seguir ilustra uma circunferência de raio medindo R e o octógono regular de lado medindo
d nela inscrito.
R
d
Dessa forma, o comprimento da circunferência pode ser aproximado por 8d. Outra possibilidade é
circunscrever um polı́gono regular, em vez de inscrever, como mostra a figura a seguir.
R
b
D
Nesse caso, o comprimento é aproximado por 8D.
14. A razão entre o comprimento exato de uma circunferência e o comprimento aproximado, obtido com
o perı́metro do octógono circunscrito, é
(a)
π
.
8·tg ( π8 )
(b)
π
8
(c)
· tg
π
tg ( π8 )
π
8
.
(d) π · tg
(e) π · tg
.
π
8 .
π
4 .
15. O método descrito no texto também permite obter uma aproximação para a área do cı́rculo. Utilizandose o octógono inscrito, a razão entre a área exata e a área aproximada do cı́rculo é
√
2.
√
(b) 2 2.
(a)
(c)
√
2
4 .
√
(d) 2π 2.
(e)
√
π 2
4 .
9
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
16. Carlos deseja sacar num caixa eletrônico uma quantia entre R$ 51,00 e R$ 99,00. O caixa dispõe de
notas de R$ 5,00, R$ 10,00 e R$ 20,00, e sempre fornece o menor número de cédulas que compõe o
valor solicitado. Dentre os valores que Carlos está disposto a sacar, apenas alguns serão feitos com
exatamente 5 cédulas. A soma desses valores é
(a) R$ 75,00.
(b) R$ 160,00.
(c) R$ 250,00.
(d) R$ 300,00.
(e) R$ 350,00.
Utilize as informações a seguir para as questões 17 e 18.
Em um jogo de azar, são sorteados 5 números, sem reposição, dentre os algarismos de 1 a 9. Esses 5
números são, então, escondidos, de modo que os participantes não os vejam. Cada participante escolhe
de um a cinco números distintos dentre os algarismos de 1 a 9 e os anota em um papel, anotando
também o valor que deseja apostar. Os números sorteados são revelados e, então, vencem as apostas
apenas os jogadores que acertarem todos os números anotados. Se mais de um jogador vencer e
esses vencedores tiverem apostado a mesma quantia, o prêmio é dividido de maneira inversamente
proporcional à probabilidade de que cada aposta fosse vencedora.
17. Numa determinada rodada, 2 jogadores que apostaram a mesma quantia venceram, sendo que um
deles escolheu 2 algarismos e, o outro, 3. Se o prêmio a ser dividido for de R$ 1.100,00, o jogador
que escolheu 2 algarismos receberá
(a) R$ 330,00.
(b) R$ 440,00.
(c) R$ 660,00.
(d) R$ 880,00.
(e) R$ 990,00.
18. Numa determinada rodada, todos os jogadores apostaram em apenas 2 números, todos eles venceram,
e nenhum deles escolheu o mesmo par de números que outro jogador. A quantidade máxima possı́vel
de vencedores nessa rodada foi de
(a) 5.
(b) 8.
(c) 10.
(d) 16.
(e) 28.
10
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
19. Em um sistema ortogonal de 3 coordenadas, a superfı́cie lateral de um sólido é descrita pela união
das seguintes regiões:
• x2 + y 2 = 4, com 0 ≤ z ≤ 3
• x2 + y 2 ≤ 4, com z = 0 ou z = 3
A área lateral e o volume desse sólido são, respectivamente,
(a) 6π e 12π.
(b) 12π e 48π.
(c) 6π e 48π.
(d) 12π e 48π.
(e) 12π e 12π.
1
20. O valor exato da expressão √2−1
, com 5 casas decimais, é 2,41421. Considere os seguintes métodos
para se fazer essa conta sem o auxı́lio da calculadora:
• Método A: usa-se um valor aproximado para
√
2 e faz-se a divisão;
• Método B: racionaliza-se o denominador e usa-se um valor aproximado para
√
2.
Ao se fazer uma aproximação, comete-se um erro, que é definido como a diferença, em módulo, entre
o valor aproximado e o valor exato.
√
Usando a melhor aproximação para 2 com uma única casa decimal, a razão entre os erros (em
relação ao valor exato) obtidos nos métodos A e B, respectivamente, é de cerca de
(a) 10.
(b) 8.
(c) 6.
(d) 4.
(e) 2.
11
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
21. O esquema a seguir representa a hierarquia dos executivos de uma grande empresa. As ligações
de uma pessoa com outra(s) abaixo dela representam relações de subordinação. Por exemplo, o
presidente da empresa, no topo do esquema, tem 4 pessoas subordinadas diretamente a ele. Dessas
4 pessoas, uma não tem subordinados (à esquerda), e as outras têm, respectivamente (da esquerda
para a direita), quatro, um e três subordinados.
R$12.000,00
R$8.000,00
R$3.000,00
R$4.000,00
R$3.000,00
R$4.000,00
R$5.000,00
R$3.000,00
R$9.000,00
R$3.000,00
R$7.000,00
R$6.000,00 R$5.000,00
R$6.000,00
R$3.000,00
Os valores indicados nos retângulos abaixo de cada pessoa são os salários mensais dessas pessoas. A
polı́tica de salários da empresa estabelece que:
• uma pessoa não pode ganhar mais do que a metade da soma dos salários de seus subordinados,
se tiver dois subordinados ou mais;
• uma pessoa que só tem um subordinado não pode ganhar mais do que o dobro desse subordinado.
De acordo com essas regras, o salário máximo que o presidente pode ter é
(a) R$25.250,00.
(b) R$26.500,00.
(c) R$27.750,00.
(d) R$29.000,00.
(e) R$30.250,00.
12
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
22. Observe o mosaico a seguir.
As peças que foram usadas para construı́-lo são identicas e têm a forma a seguir.
a
b
c
A relação entre as medidas a, b e c é
√
(a) a = 2b e b = c 2.
√
√
(b) a = b 3 e b = c 2.
(c) a = 3b e b = c.
(d) a = 2b e b = c.
√
(e) a = b 3 e b = 2c.
13
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
Utilize as informações a seguir para as questões 23 e 24.
A tabela a seguir apresenta a distribuição das notas dos alunos de uma disciplina da faculdade de
Administração nas duas provas realizadas por eles.
Nota
4
5
6
7
8
9
Prova 1 (quantidade de alunos)
10
10
25
10
10
10
Prova 2 (quantidade de alunos)
5
5
20
20
20
5
23. A nota final de cada aluno deve ser calculada considerando peso de 25% para a prova 1 e de 75%
para a prova 2. A média das notas finais de todos os alunos é igual a
(a) 6,4.
(b) 6,5.
(c) 6,6.
(d) 6,7.
(e) 6,8.
24. O percentil da nota de um aluno em uma prova é a porcentagem de pessoas que obtiveram, naquela
prova, uma nota igual ou inferior à nota desse aluno. Se a nota de um aluno na prova 2 foi 7, então
o percentil dessa nota é, aproximadamente,
(a) 51%.
(b) 55%.
(c) 59%.
(d) 63%.
(e) 67%.
25. Considere a seguinte sequência de figuras formadas a partir de pontos.
1a figura
2a figura
3a figura
4a figura
5a figura
Para escrever a 30a figura dessa sequência, a quantidade de pontos adicionais que devem ser utilizados
em relação ao que é necessário para escrever a 29a figura é igual a
(a) 55.
(b) 56.
(c) 57.
(d) 58.
(e) 59.
14
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
26. Um analista de recursos humanos desenvolveu o seguinte modelo matemático para relacionar os anos
de formação (t) com a remuneração mensal (R) de uma pessoa ao ingressar no mercado de trabalho:
R = k(1, 1)t ,
em que k é um fator de carreira, determinado de acordo com a área que a pessoa estudou. A tabela
a seguir apresenta os anos de formação e os correspondentes fatores de carreira de três pessoas (A, B
e C).
Pessoa
A
B
C
Anos de Formação (t)
18
16
19
Fator de Carreira (k)
500
600
500
Se as remunerações mensais das pessoas A, B e C são, respectivamente, RA , RB e RC , então, de
acordo com esse modelo,
(a) RB < RA < RC .
(b) RA < RB < RC .
(c) RA = RB < RC .
(d) RC < RB < RA .
(e) RB < RC = RA .
27. Sejam An e Bn , com n ∈ N∗ , valores definidos por:
• An = 1 + 2 + 4 + 8 + 16 + . . . + 2n−1
• Bn = 3 + 5 + 7 + 9 + 11 + . . . + (2n + 1)
O valor de A30 + B30 é igual a
(a) 229 + 261.
(b) 229 + 260.
(c) 230 − 960.
(d) 230 + 960.
(e) 230 + 959.
Utilize as informações a seguir para as questões 28 e 29.
Uma estação de trens é constituı́da por dois galpões cujas fachadas têm a forma de dois semicı́rculos
que se tangenciam, conforme a figura a seguir.
Terminal 1
Terminal 2
Os raios dos semicı́rculos das fachadas dos terminais 1 e 2 medem, respectivamente, 30m e 20m. Uma
empresa está fazendo um estudo para instalar um sistema de ar condicionado nos galpões.
15
B
Vestibular Insper 2014 2
Análise Quantitativa e Lógica
28. Para dimensionar o sistema de renovação do ar, uma das informações necessárias é o volume total
dos galpões, que têm a forma de semicilindros. Se a distância entre as fachadas e os fundos é 100
metros, esse volume é aproximadamente igual a
(a) 50.000m3
(b) 100.000m3
(c) 150.000m3
(d) 200.000m3
(e) 250.000m3
29. Para diminuir o impacto da insolação, pretende-se instalar um telhado tangenciando os dois terminais conforme indicado pela linha tracejada na figura. A medida do telhado, correspondente ao
comprimento dessa linha tracejada, é igual a
√
(a) 60 3m
√
(b) 60 2m
√
(c) 30 2m
√
(d) 20 3m
√
(e) 20 6m
30. Um economista analisou dados históricos sobre o valor das ações de uma empresa e, com o intuito
de prevê-lo ao longo do ano de 2014, elaborou o seguinte modelo:
V (t) = 2 · sen
π·t π
−
180
4
+ 3 · sen
π·t π
−
20
4
Na função acima, V é o valor da ação e t é o tempo decorrido, em dias, a partir do inı́cio do ano (ou
seja, t = 1 denota o fim do dia 1o de janeiro de 2014). Para simplificar, suponha que todos os meses
tenham 30 dias. De acordo com esse modelo, a ação deve atingir seu preço máximo ao término do
dia
(a) 10 de janeiro.
(b) 30 de julho.
(c) 15 de julho.
(d) 30 de março.
(e) 15 de maio.
31. O número de soluções reais da equação
é
2
log2 (x2 + 1) − 34 log2 (x2 + 1) + 64 = 0
(a) 1.
(b) 2.
(c) 3.
(d) 4.
(e) 5.
16
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
Utilize as informações a seguir para as questões 32 e 33.
Os analistas responsáveis pelas estratégias comerciais de uma grande rede de lojas propuseram a
seguinte regra para conceder descontos aos clientes:

0, 90v , se v ≤ 100
p(v) = 0, 80v , se 100 < v ≤ 200 ,

0, 70v , se v > 200
em que v é o soma dos valores marcados nos produtos que o cliente comprar e p(v) é o pagamento
que o cliente deverá fazer no caixa, com desconto sobre essa soma.
32. Dois clientes passaram pelo caixa e pagaram R$90,00, mas os valores totais das compras deles antes
de ser aplicado o desconto eram diferentes. A diferença entre esses valores totais é de
(a) R$12,50.
(b) R$15,00.
(c) R$17,50.
(d) R$20,00.
(e) R$22,50.
33. O departamento de marketing precisa criar uma tabela para comunicar as condições dos descontos
para os clientes. Das opções abaixo, aquela que explica corretamente a regra proposta pelos analistas
é
(a)
Se o valor da sua compra é...
menor do que R$100,00
menor do que R$200,00 e maior ou igual a R$100,00
maior ou igual a R$200,00
...seu desconto é de...
90%
80%
70%
(b)
Se o valor da sua compra é...
menor ou igual a R$100,00
menor ou igual a R$200,00 e maior do que R$100,00
maior do que R$200,00
...seu desconto é de...
90%
80%
70%
(c)
Se o valor da sua compra é...
menor do que R$100,00
menor do que R$200,00 e maior ou igual a R$100,00
maior ou igual a R$200,00
...seu desconto é de...
10%
20%
30%
(d)
Se o valor da sua compra é...
menor ou igual a R$100,00
menor ou igual a R$200,00 e maior do que R$100,00
maior do que R$200,00
...seu desconto é de...
10%
20%
30%
(e)
Se o valor da sua compra é...
menor ou igual a R$100,00
menor ou igual a R$200,00 e maior do que R$100,00
maior do que R$200,00
...seu desconto é de...
30%
20%
10%
17
Vestibular Insper 2014 2
B
Análise Quantitativa e Lógica
34. O grêmio de uma faculdade convidou os alunos do primeiro semestre para uma atividade de integração.
Eles contaram os calouros presentes e tentaram agrupá-los de forma que todos os grupos tivessem
a mesma quantidade de pessoas, mas não havia maneira de fazê-lo, pois não queriam apenas uma
pessoa por grupo e nem um único grande grupo. Pode-se concluir que a quantidade de calouros era
necessariamente um número
(a) par.
(b) quadrado perfeito.
(c) primo.
(d) menor do que 300.
(e) maior do que 50.
35. O gráfico a seguir mostra os resultados de uma pesquisa sobre o governo brasileiro.
(Fonte: http://g1.globo.com/politica/noticia/2013/08/avaliacao-de-dilma-sobe-de-31-para-38-diz-ibope.html)
A maior variação positiva, em pontos percentuais, entre dois meses consecutivos ocorreu
(a) na opção “regular” entre os meses de março e junho.
(b) na opção “ruim/péssimo” entre os meses de junho e julho.
(c) na opção “ótimo/bom” entre os meses de junho e julho.
(d) na opção “regular” entre os meses de julho e agosto.
(e) na opção “ruim/péssimo” entre os meses de julho e agosto.
18