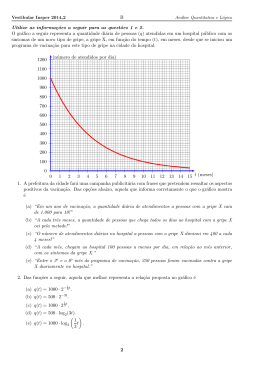
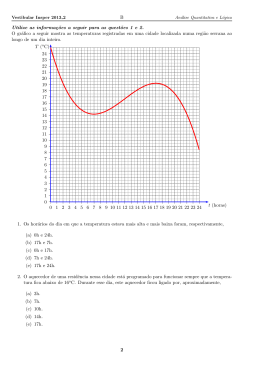
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
1. Considere o polinômio p(x) = −x3 − 4x + 5x2 + 20.
(a)
Fatore a expressão ax + bx + ay + by.
(b)
Determine as três raı́zes de p(x).
1
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
2. Um rapaz listou os programas que ele mais gosta de fazer aos sábados e domingos
e criou um ı́ndice mensal de diversão para classificá-los. Ele classifica cada passeio
levando em consideração o quanto ele gosta de fazê-lo e se é a primeira, a segunda,
a terceira ou a quarta vez que ele o faz num determinado mês. Assim, o programa
mais divertido feito pela primeira vez num mês recebe nota 10 e um programa que
se repete muitas vezes num mês pode até receber nota 0. A tabela abaixo mostra
cada um dos programas que o rapaz costuma fazer com seus respectivos ı́ndices de
diversão (dependendo da repetição no mês), assim como o dinheiro que ele gasta
com cada programa.
No de vezes no mês
1
Cinema com boliche 7
Praia
9
Danceteria
10
(a)
2
5
8
6
3 4 ou mais
Custo
4
1
R$40,00
2
0
R$100,00
3
0
R$50,00
Se em novembro de 2004 o rapaz dispõe de dinheiro suficiente para fazer
qualquer um dos programas da tabela acima em qualquer sábado ou domingo do mês, determine quantas vezes ele deve fazer cada programa neste
mês para maximizar sua diversão acumulada.
2
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
(b)
Determine quantas vezes ele deve fazer cada programa para acumular pelo
menos 40 pontos de diversão num determinado mês, com o menor custo
possı́vel. Não é necessário que o rapaz faça um passeio em cada sábado e
em cada domingo do mês.
3
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
3. Considere a palavra IBMEC.
(a)
Determine quantas palavras podem ser formadas utilizando, sem repetição,
uma, duas, três, quatro ou as cinco letras dessa palavra. (Por exemplo, I,
BC, MEC, CEM, IMEC e a própria palavra IBMEC devem incluı́das
nesta contagem.)
(b)
Colocando todas as palavras consideradas no item anterior em ordem alfabética, determine a posição nesta lista da palavra IBMEC.
4
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
4. A figura abaixo representa o cruzamento perpendicular de duas rodovias, com sentidos de tráfego devidamente indicados. Suponha que todas as pistas têm largura
de dez metros e que as curvas que delimitam as interligações são arcos de circunferências, perfeitamente ajustadas de modo a tangenciarem as linhas tracejadas que
dividem as duas pistas de cada rodovia (neste caso com raio de 30 metros), ou duas
retas que dão delimitações externas das rodovias (neste caso com raio de 20 metros).
A
N
O
L
S
(a)
Determine a área da região sombreada, onde deve ser plantado um gramado.
5
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
(b)
Uma viajante que está no ponto A, portanto seguindo de leste para oeste,
gostaria de passar uma única vez por todas pistas de interligação deste
cruzamento, retornando em seguida para o ponto A. Determine quantos
metros esta viajante irá percorrer neste passeio, supondo que ela sempre irá
andar no meio da pista.
6
Análise Quantitativa e Lógica Discursiva - Prova A
Vestibular Ibmec São Paulo 2005 1
Nome:
5. Seja a um número real positivo. Considere que na figura abaixo PS⊥QR.
y
P
a+3
R
a+1
a
Q
a+1
a
(a)
S
x
a+3
Desenvolva o determinante
a
a
+
3
1
a
1 .
D = a + 1
a + 3 a + 1 1
(b)
Determine a medida da altura PS relativa ao lado QR do triângulo PQR
em função de a.
7
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
b
b
b e AEF
b
6. Na figura abaixo, AB = 1cm, AC = 2cm e os ângulos ABC,
ACD,
ADE
são todos congruentes.
D
A
C
B
F
(a)
Determine o perı́metro do polı́gono BCDEF.
8
E
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
(b)
b
Se α é a medida do ângulo FCB,
determine cos(α). Se necessário, utilize
cos(a − b) = cos(a)cos(b) + sen(a)sen(b).
9
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
7. Considere a função dada por f (x) = x2 − 6x + 8.
(a)
Determine o valor mı́nimo desta função, assim como os pontos de intersecção
do gráfico da função com a reta y = 1.
(b)
Determine as raı́zes da função g(x) = |x2 − 6x + 8| − 1.
10
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
8. Sejam a e b números reais positivos.
(a)
Resolva na variável t a equação
t + (b − a) −
(b)
ab
= 0.
t
Resolva na variável x a equação
x−a+b−
11
ab
= a.
x−a
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
9. Considere que x é um número positivo.
(a)
Desenvolva o determinante
log2 x 0 2 x
1 4 .
x
2
2 16
(b)
Determine os pontos de intersecção dos gráficos das funções
f (x) = 8 log2 x + 4x
e
g(x) = 2x+1 .
12
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
10. Sabe-se que entre os agentes Mileum, Miledois e Miletrês do Serviço Secreto Vitruviano há um espião (e apenas um). Estes três agentes trabalham em equipe da
seguinte maneira:
• cada um deles recebe duas mensagens, que sempre são sentenças (ou seja,
declarações que somente podem ser verdadeiras ou falsas),
• cada mensagem vem endereçada a um dos outros dois membros da equipe,
• assim, cada uma das duas mensagens deve ser fielmente transmitida pelo agente
que a recebeu para os outros dois membros da equipe, cada uma para seu
destinatário.
Ainda não se sabe qual dos três é o espião, mas já foi descoberto que o espião
transmite sempre as negações das mensagens que ele recebe, no lugar das sentenças
originais. Dessa forma, para desmascará-lo foram enviadas seis mensagens verdadeiras para os agentes, duas para cada um, que deveriam circular conforme o esquema
acima apresentado. A transmissão das informações entre os agentes foi registrada
abaixo:
Mileum→Miledois: Eu não sou o espião e Miletrês também não é.
Mileum→Miletrês: Você não é o espião.
Miledois→Mileum: Se Miletrês não é o espião, então o espião é você.
Miledois→Miletrês: Mileum é o espião.
Miletrês→Mileum: Miledois é o espião.
Miletrês→Miledois: Se eu não sou o espião, então Mileum também não é.
Determine quem é o espião, justificando seu raciocı́nio.
13
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
Rascunho
Rascunho
Rascunho
14
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
Rascunho
Rascunho
Rascunho
15
Vestibular Ibmec São Paulo 2005 1
Análise Quantitativa e Lógica Discursiva - Prova A
Nome:
Rascunho
Rascunho
Rascunho
16