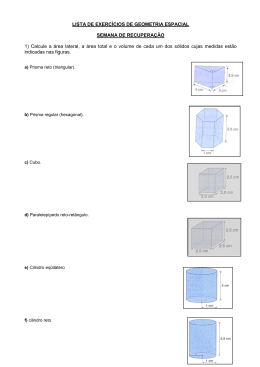
EXERCÍCIOS DE FIXAÇÃO – GEOMETRIA SÓLIDA
ÁREAS E VOLUMES DE PRISMAS, CILINDROS E CONES
2a SÉRIE – ENSINO MÉDIO
2011
==========================================================================================
1) Em cada Prisma representado a seguir, calcule a área da base (Ab), a área lateral
(AL), a área total (AT) e o volume (V):
a)
b)
Bases: triângulos
Eqüiláteros com 4 cm
de lado.
Aresta lateral medindo 6 cm .
Medidas das arestas:
2 cm, 4 cm e 6 cm
c)
Prisma reto cujas bases são
triângulos retângulos de lados
medindo 2√2 m, 1 m e 3 m.
A aresta lateral mede 4 m.
e)
d)
Prisma reto cujas bases são
hexágonos regulares com 2 dm
de lado. A aresta lateral mede
2√3 dm
Piscina cuja superfície d’água é um
retângulo de lados medindo 4m e
16m; altura da parte rasa igual a 1m
E altura da parte funda igual a 3 m.
2) Sabe-se que:
► Um recipiente com 1 cm3 de volume tem uma capacidade de 1mℓ.
► Um recipiente com 1 dm3 de volume tem uma capacidade de 1ℓ.
► Um recipiente com 1 m3 de volume tem uma capacidade de 1.000ℓ.
Calcule a capacidade de cada prisma do exercício anterior.
3) Veja o cálculo da diagonal de um prisma famoso: O Paralelepípedo.
Observe que na figura temos um paralelepípedo cujo
comprimento ,largura e altura medem, respectivamente a ,
b e c , a diagonal do paralelepípedo mede D e digamos
que a diagonal da base inferior mede x . Então , temos pelo
teorema de pitágoras :
D2 = x2 + c2 , mas também x2 = a2 + b2 . Então , temos
D2 = a2 + b2 + c2 e , finalmente : D = a 2 + b 2 + c 2
a) Calcule a diagonal do paralelepípedo do exercício 1-a.
b) Calcule a diagonal de um cubo com 2√3 dm de aresta.
c) a soma das medidas de todas as arestas de um cubo é 120 cm. Calcule a medida da
diagonal do cubo.
d) Num paralelepípedo retângulo de base quadrada, a soma das medidas de todas as
arestas é 40 m. calcule a diagonal do paralelepípedo, sabendo que cada aresta da base é
o dobro de cada aresta lateral.
4) As dimensões de um paralelepípedo retângulo são dadas por números inteiros em
P.A. de razão igual a 2 cm . Se a diagonal do paralelepípedo mede , em centímetros ,
10 2 , calcule sua capacidade em litros .
5) Calcule a área total de um cubo cuja diagonal mede 3 m .
6) Num paralelepípedo retângulo , uma das dimensões da base é o dobro da outra .
Se a área lateral é de 88 dm2 , calcule o volume do paralelepípedo .
7) Num aquário em forma de paralelepípedo retângulo cuja base é um quadrado
com 1 m2 de área , mergulha-se completamente uma pedra de modo que o nível da
água se eleva em 1 mm . Se a pedra tem o formato de um cubo , calcule a medida da
aresta desse cubo .
8) (U.F.MG) - Uma piscina tem 25 m de largura , 50 m de comprimento,1,5 m de
profundidade numa das extremidades e 2,5 m na outra . Seu fundo é um plano
inclinado. Calcule o volume da piscina .
9) (U.F.MG) - Dois prismas oblíquos , de mesma altura h , têm um quadrado de lado a
como base inferior comum e suas bases superiores têm apenas uma aresta comum de
acordo com a figura. Calcule o volume do sólido formado pela interseção dos dois
prismas.
10) (U.F.MG) - A base de uma paralelepípedo é uma região retangular cujos lados
medem 20 cm e 4 2 cm .As extremidades são duas faces quadradas que fazem um
ângulo de 45o com a base . Um plano perpendicular à aresta maior intercepta o
paralelepípedo segundo uma região retangular . Qual é a área total do paralelepípedo ?
(veja a figura a seguir)
11) (PUC-MG) - Na figura , o cubo tem aresta 4 cm e BP = 2 cm está sobre o
prolongamento da aresta AB.Qual é a medida do segmento PG ?
12) (U.F.MG) - Na figura , está representado um cubo de aresta 10 . Sabendo que
AP = QC = 4 , calcule a distância de P a Q .
13) Uma torneira despeja 3.000 litros/min de um líquido inflamável num
compartimento da carroceria de um caminhão. Quanto tempo será necessário para
ocupar o volume ideal do compartimento, que é de 95%, se esse compartimento tem
a) o formato e as dimensões dos prismas do exercício 1.c, 1.d e 1.e ?
b) o formato, com as dimensões em metros do prisma do exercício 10.
14) Um chocolate em barra é fabricado caseiramente por uma família. Cada barra é
vendida com um lucro de 40% sobre o preço de custo. O custo refere-se ao preço do
chocolate mais o preço da embalagem, sendo que o chocolate custa R$ 0,90 cada porção
de 2 cm3 e o papel que embala, sem sobra, a barra de chocolate custa R$ 0,05 cada
pedaço de 5 cm2. Se a barra de chocolate tem o formato e as dimensões do prisma do
exercício 1.b (use √3 = 1,7), por quanto é vendida cada barra?
15) Calcule a área da base (Ab), a área lateral (AL), a área total (AT) e o volume (V) de
cada sólido apresentado a seguir:
a)
Cilindro circular reto com 6 cm de raio da base e
12 cm de altura.
b)
Cilindro eqüilátero (diâmetro da base = altura) com
3π dm de perímetro da base.
c)
Cilindro circular reto cujo diâmetro da base
é o dobro da altura e cujo perímetro da base
é 30 cm, se π = 3.
d) Sólido gerado pela rotação do quadrado ABCD em torno do seu lado AD, sendo 8 m
a medida do lado.
A
B
D
C
e) Sólido gerado pela rotação do polígono ABCDEF em torno do seu lado AF, sendo
AF = 10 dm, DE = 4 cm, AB = 5 cm e EF = 12 cm.
A
B
C
F
D
E
e)
Cone circular reto com 5 dm de raio da base
E √11 dm de altura
f) Cone circular reto com 10 cm de geratriz e 12 cm de diâmetro da base.
g) Cone eqüilátero com 10π km de perímetro da base.
h) Cone circular reto cuja área lateral é 60 m2 e cuja geratriz tem 1 m a mais do que o
triplo da medida do raio da base. (considere π = 3).
i) Sólido gerado pela rotação do triângulo retângulo ABC em torno do cateto AC, sendo
AC = 12 cm e AB = 15 cm.
A
C
B
j) Sólido gerado pela rotação do polígono ABCDE em torno de AE, sendo AE = 12 m,
CD = 5 m, ED = 6 m e BC = 3 m.
A
B
C
E
D
16) Uma torneira enche até a borda uma piscina circular de profundidade única em 1
dia, despejando 9.000 litros por hora. Se o raio da piscina é 6 m, qual é a sua
profundidade? (Use π = 3)
17) Um pirulito tem o formato exato de um cone circular reto com 6 cm de altura e 2 cm
de diâmetro da base. O pirulito é fabricado exclusivamente com açúcar, que custa R$
1,80 o quilo, sendo que cada quilo, depois de derretido, rende 0,7 dm3. Por outro lado, o
pirulito, depois de esfriado é embalado com papel manteiga colado em toda a sua
superfície. Se o papel manteiga custa R$ 0,50 cada dm2, qual é o custo total do pirulito,
sem a mão de obra?
18) (U.F.MG ) - Observe a figura que se segue . Nessa figura , AB = 1 , BC = 3 e BD
=
9
. Calcule o volume do sólido gerado girando de 360o , em torno da reta AE , a
4
região do plano cujo contorno é
a) o triângulo ACE ;
b) o triângulo BCD.
19) (U.F.MG) - A área da base de um cilindro circular reto é 16π cm2 esua área lateral é
250 cm2 . Calcule o tempo necessário para enchê-lo de água usando-se uma torneira de
vazão 5 cm3/s .
20) (U.F.MG) - As áreas das superfícies laterais de dois cilindros retos V1 e V2 , de
bases circulares , são iguais . Se as alturas e os raios das bases dos dois cilindros são ,
respectivamente , H1 , R1 , H2 e R2 , calcule a razão entre os volumes de V1 e V2 , nesta
ordem .
21) (U.F.MG) - Um cilindro reto , cuja altura é igual ao diâmetro da base , a área de
uma secção perpendicular às bases , contendo os centros dessas , é 64 m2 . Calcule a
área lateral do cilindro.
22) (U.F.MG) - Na figura a seguir , o cilindro reto , de altura igual ao diâmetro da base ,
é cortado por um plano paralelo ao seu eixo e à distância d = 3 cm do mesmo . A área
da secção determinada pelo plano é 80 cm2 . Calcule a área lateral do cilindro .
23) (PUC - MG ) - A região plana limitada pelo retângulo ABCD gira em torno do
lado AB e gera um cilindro de volume V1 . A mesma região , ao girar em torno do lado
BC , gera um outro cilindro de volume V2 . Se AB = 4 cm e BC = 6 cm , determine V1
em função de V2 .
D
C
A
B
24) (U.F.MG ) - As medidas da geratriz , do raio da base e da altura de um cone
circular reto são x + a , x e x - a , respectivamente . Ao calcular o volume do cone ,
usou-se , por engano , a fórmula do cilindro circular reto de mesmo raio e mesma altura
do cone . O valor encontrado supera em 4π cm3 o volume procurado. Calcule a altura e
o raio da base do cone.
25) (PUC - MG) - Na figura , a região limitada pelo triângulo ABC faz um giro de 60o
em torno da reta AB . Sendo AB = 2.(AC) = 6 cm , calcule o volume do sólido
gerado.
26) (U.F.J.F. -MG) - Uma pessoa bebeu vinho em um cálice em forma de cone.
Estando o cálice cheio até a borda e tendo a pessoa bebido até o nível do vinho ficar
exatamente na metade da altura do cálice , calcule a fração do volume total do vinho
consumido .
27) (U.F.U. - MG) - Considere um tanque cilíndrico de 6 metros de comprimento e 2
metros de diâmetro que está inclinado em relação ao solo em 45o , conforme mostra a
figura abaixo . Sabendo-se que o tanque é fechado na base que toca o solo e aberto na
outra, qual é o volume máximo de água que o tanque pode conter antes de derramar?
28) (F.C.M.MG) - Na figura , o recipiente de altura H é um cone circular reto de base
horizontal e raio R . O líquido no recipiente ocupa
1
do volume deste . Calcule o nível
8
h do líquido no recipiente , em função de H .
29) (U.F.V -MG) - O trapézio retângulo abaixo sofre uma rotação de 360o em torno da
base maior . Sabendo-se que AB = 3 cm , CE = 5 cm e que o volume do sólido obtido é
84π cm3 , determine AC .
30) (PUC - MG ) - Um cone reto de raio r = 4 cm tem um volume equivalente ao de
um prisma de altura h = 12 cm e de base quadrada de lado ℓ = √π . Calcule a altura do
cone.
**********************************************************************
RESPOSTAS DAS QUESTÕES DE VESTIBULARES:
18) a) 16π b) 27π/2
19) 1 min 40 s
20) R1/R2
21) 64π m2
22) 100π cm2
23) V1=3V2/2
24) h = 3/2 e r = 2
25) 3π m3
26) (7/8)Vtotal
27) ) 5π m3
28) H/2
29) AC = 8 cm
30) 2,25 cm.