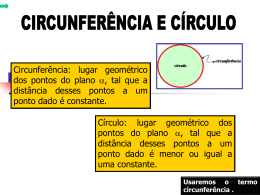
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 1
I.GEOMETRIA
1. PONTO, RETA E PLANO
Podemos ilustrar com as seguintes idéias para entender alguns conceitos primitivos em
Geometria:
1.
Na figura acima, a reta t é transversal às retas m e n e estas três retas
formam 8 ângulos, sendo que os ângulos 3, 4, 5 e 6 são ângulos internos e
os ângulos 1, 2, 7 e 8 são ângulos externos. Cada par destes ângulos,
recebe nomes de acordo com a localização em relação à reta transversal e
às retas m e n.
PONTO:
uma estrela, um pingo de caneta, um furo de agulha, ...
3.
PLANO:
o quadro negro, a superfície de uma mesa, ...
2.
RETA:
fio esticado, lados de um quadro, ...
2. ÂNGULOS
Tipos:
Retas paralelas : não possuem qualquer ponto em comum.
Retas concorrentes : possuem um único ponto em comum
Retas perpendiculares : retas concorrentes que formam ângulos de 90 graus
Retas transversais e ângulos especiais: é uma reta que tem interseção com
as outras retas em pontos diferentes.
1.
DEFINIÇÃO:
região do plano limitada por duas semirretas de
mesma origem. As semirretas recebem o nome
de lados do ângulo e a origem delas, de vértice
do ângulo.
2.
UNIDADES:
grau, símbolo º,
submúltiplos = minuto „ e o segundo “.
1º (grau) = 60‟ (minutos) e
1‟ = 60”(segundos).
Transferidor = objeto capaz de medir o valor de um ângulo.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 2
5.
3.
CLASSIFICAÇÃO DE ÂNGULOS
RETAS PARALELAS CORTADAS POR UMA
TRANSVERSAL
Os ângulos são classificados de acordo com suas medidas:




Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.
Ângulos correspondentes: a e e, d e h, b e f, c e g
Ângulos colaterais externos: a e h, b e g
Ângulos colaterais internos: e e d, c e f
Ângulos alternos externos: a e g, b e h
Ângulos alternos internos: d e f, c e e
agudo
4.
reto
obtuso
raso
BISSETRIZ DE UM ÂNGULO
semirreta que se origina no vértice do ângulo principal, dividindo-o em
outros dois ângulos com medidas iguais.
6.
Congruentes
Suplementares
Suplementares
Congruentes
Congruentes
EXERCICOS DE ÂNGULOS
01 – encontre os ângulos:
As retas f e g são paralelas (f // g). Determine a medida do ângulo â, nos
seguintes casos:
a)
b)
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 3
Obtenha as medidas dos ângulos assinalados
Resp.: 55º
Resp: 74º
d) As retas a e b são paralelas.
Quanto mede o ângulo î?
c
Resposta:
160° - 3x = x + 100°
160° - 100° = x + 3x
60° = 4x
x = 60°/4
x = 15°
Então 15°+100° = 115° e 160°-3*15°
= 115°
Resp: 33º
Resposta:
6x + 15° + 2x + 5º = 180°
6x + 2x = 180° -15° - 5°
8x = 160°
x = 160°/8
x = 20°
Então, 6*20°+15° =135° e 2*20°+5°
= 45°
Resposta:
Imagine uma linha cortando o
ângulo î, formando uma linha
paralela às retas "a" e "b".
Fica então decomposto nos ângulos
ê e ô.
Sendo assim, ê = 80° e ô = 50°,
pois o ângulo ô é igual ao
complemento de 130° na reta b.
Logo, î = 80° + 50° = 130°
Resposta:
Sabemos que a figura tem 90°.
Então x + (x + 10°) + (x + 20°) + (x +
20°) = 90°
4x + 50° = 90°
4x = 40°
x = 40°/4
x = 10°
Usando uma equação, determine a
medida de cada ângulo do triângulo:
d)
Resposta:
Sabemos
que
os
ângulos
laranja+verde formam 180°, pois são
exatamente a metade de um círculo.
Então, 138°+x = 180°
x = 180° - 138°
x = 42°
Logo, o ângulo x mede 42°.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 4
Sabemos que a soma dos ângulos
do triângulo é 180°.
Então, 6x + 4x + 2x = 180°
12x = 180°
x = 180°/12
x = 15°
Os ângulos são: 30°, 60° e 90°.
1.
POLÍGONO:
É uma figura plana formada por três ou mais segmentos de reta que se
intersectam dois a dois.
lados
segmentos de reta
vértices
pontos de intersecção
3. GEOMETRIA PLANA:
polígono
região interior
Introdução
Os estudos iniciais sobre Geometria Plana estão relacionados à Grécia Antiga, também
pode ser denominada Geometria Euclidiana em homenagem a Euclides de Alexandria
(360 a.C. - 295 a.C.), grande matemático educado na cidade de Atenas e freqüentador da
escola fundamentada nos princípios de Platão.
Elementos de geometria plana
Podemos relacionar à Geometria plana os seguintes conteúdos programáticos:
 Ponto, reta e plano
 Posições relativas entre retas
 Ângulos
 Triângulos
 Quadriláteros
 Polígonos
 Perímetro
 Áreas de regiões planas
4. TRIÂNGULOS OU TRILÁTERO
1.
COCEITOS
Definição:
Triângulo é um polígono de três lados. É o polígono que possui o menor
número de lados.
Elementos:
Vértices:
A,B,C.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 5
Lados:
AB,BC e AC.
Ângulos internos:
a, b e c.
Altura:
BH é uma altura do triângulo.
Triângulo
Isósceles
Dois lados têm a mesma medida.
m(AB)=m(AC)
Triângulo
Escaleno
Todos os três lados têm medidas
diferentes.
Mediana:
É o segmento que une um vértice ao ponto médio do
lado oposto.
Classificação dos triângulos quanto às medidas dos ângulos
BM é uma mediana.
Bissetriz:
É a semi-reta que divide um ângulo em duas
partes iguais. O ângulo B está dividido ao meio e
neste caso Ê = Ô.
Ângulo Interno:
É formado por dois lados do triângulo. Todo
triângulo possui três ângulos internos.
Ângulo Externo:
É formado por um dos lados do triângulo e pelo
prolongamento do lado adjacente(ao lado).
2.
CLASSIFICAÇÃO
Classificação dos triângulos quanto ao número de lados
Triângulo
Eqüilátero
Os três lados têm medidas iguais.
m(AB)=m(BC)=m(CA)
3.
Triângulo
Acutângulo
Todos os ângulos internos são agudos,
isto é, as medidas dos ângulos são
menores do que 90º.
Triângulo
Obtusângulo
Um ângulo interno é obtuso, isto é,
possui um ângulo com medida maior do
que 90º.
Triângulo
Retângulo
Possui um ângulo interno reto (90 graus).
MEDIDAS DOS ÂNGULOS DE UM TRIÂNGULO
Ângulos Internos:
Consideremos o triângulo ABC. Poderemos identificar com as letras a, b e c
as medidas dos ângulos internos desse triângulo.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 6
A soma dos ângulos internos de qualquer triângulo é sempre igual a 180
graus, isto é:
a + b + c = 180º
Exemplo:
Considerando o triângulo abaixo, podemos escrever que: 70º+60º+x=180º e
dessa forma, obtemos x=180º-70º-60º=50º.
a: hipotenusa
b e c: catetos
h: altura relativa a hipotenusa
m e n: projeções ortogonais dos catetos sobre a hipotenusa.
Ângulos Externos:
triângulo ABC. as letras maiúsculas representam os ângulos externos.
Relações métricas
- O quadrado de um cateto é igual ao produto da hipotenusa pela projeção
desse cateto sobre a hipotenusa.
b² = a.n
Todo ângulo externo de um triângulo é igual à soma dos dois ângulos
internos não adjacentes a esse ângulo externo. Assim:
A = b+c, B = a+c, C = a+b
Exemplo:
No triângulo desenhado ao lado: x=50º+80º=130º.
4.
TRIÂNGULO RETÂNGULO
todo triângulo que tem um ângulo reto.
c² = a.m
- O produto dos catetos é igual ao produto da hipotenusa pela altura relativa
a hipotenusa.
b.c = a.h
- O quadrado da altura é igual ao produto das projeções dos catetos sobre a
hipotenusa.
h² = m.n
- O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
a² = b² + c²
Exemplo:
Neste triângulo ABC, vamos calcular a, h, m e n:
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 7
a² = b² + c²
→ a² = 6² + 8² → a² = 100 → a = 10
b.c = a.h
→ 8.6 = 10.h → h = 48/10 →h = 4,8
c² = a.m
→ 6² = 10.m → m = 36/10→ m = 3,6
b² = a.n
→ 8² = 10.n → n = 64/10 → n = 6,4
5.
TRIÂNGULO EQÜILÁTERO
Dado o triângulo ABC de lado a e altura h.
5. EXERCICIOS
Determine os valores literais indicados nas figuras:
a)
a² = b² + c²
13² = 12² + x²
169 = 144 + x²
x² = 25
x=5
Para calcularmos a sua área precisamos do valor da base, que é a, e o valor
da altura, que iremos calcular da seguinte forma:
A altura de um triângulo eqüilátero divide-o em dois triângulos retângulos,
assim, se pegarmos um desses triângulos e aplicarmos o Teorema de
Pitágoras obteremos o valor da altura:
altura (h):
b.c = a.h
5.12 = 13.y
y = 60/13
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 8
b)
a² = b² + c²
c)
c² = a.m
Determine a altura de um triângulo eqüilátero de lado l.
Determine x nas figuras.
a)
d)
O triângulo ABC é eqüilátero.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 9
b)
O triângulo ABC é eqüilátero.
Exercícios resolvidos:
2) Calcule a altura de um triângulo eqüilátero que tem 10 cm de lado.
Solução:
c)
3) A altura de um triângulo eqüilátero mede 4 cm. Calcule:
a) A medida do lado do triângulo
b) A área do triângulo
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 10
4) Calcule x indicado na figura
Solução:
Solução:
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 11
forma com essa parede um ângulo de 60°. Qual é o comprimento da escada
em metros?
8) Observe na figura os três quadrados identificados por 1,2 e 3. Se a área
do quadrado 1 é 36cm² e a área do quadrado 2 é 100cm², qual é, em
centímetros quadrados, a área do quadrado 3 ?
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 12
10) Sabe-se que, em qualquer triângulo retângulo, a medida da mediana
relativa à hipotenusa é igual à metade da medida da hipotenusa. Se um
triângulo retângulo tem catetos medindo 5cm e 2cm, calcule a
representação decimal da medida da mediana relativa a hipotenusa nesse
triângulo.
A2 = A 1 + A3
100 = 36 + A2
A2 = 100 – 36 = 64cm²
9)As raízes da equação x² - 14x + 48 = 0 expressam em centímetros as
medidas dos catetos de um triângulo retângulo. Determine a medida da
hipotenusa e o perímetro desse triângulo.
11) Um quadrado e um triângulo eqüilátero têm o mesmo perímetro. Sendo
h a medida da altura do triângulo e d a medida da diagonal do quadrado.
Determine o valor da razão h/d.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 13
As ampliações e as reduções fotográficas são figuras semelhantes. Para os
triângulos:
os três ângulos são respectivamente congruentes, isto é:
A~R, B~S, C~T
Casos de Semelhança de Triângulos
Dois ângulos congruentes:
Se dois triângulos tem dois ângulos correspondentes congruentes, então os
triângulos são semelhantes.
Se A~D e C~F então: ABC~DEF
Dois lados congruentes:
Se dois triângulos tem dois lados correspondentes proporcionais e os
ângulos formados por esses lados também são congruentes, então os
triângulos são semelhantes.
6.
SEMELHANÇA DE TRIÂNGULOS
Duas figuras são semelhantes quando têm a mesma forma, mas não
necessariamente o mesmo tamanho.
Se duas figuras R e S são semelhantes, denotamos: R~S.
Exemplo:
Como
m(AB) / m(EF) = m(BC) / m(FG) = 2
então ABC ~ EFG
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 14
Exemplo:
Na figura abaixo, observamos que um triângulo pode ser "rodado" sobre o
outro para gerar dois triângulos semelhantes e o valor de x será igual a 8.
a)
x + 70o + 60o = 180º → x = 180o - 130o → x = 50o
b)
Realmente, x pode ser determinado a partir da semelhança de triângulos.
Identificaremos os lados homólogos e com eles construiremos a proporção:
3
4
=
6
x
Três lados proporcionais:
Resolução:
Devemos escolher um dos segmentos apontados na figura para prolongar, a fim de
encontrarmos dois triângulos:
Se dois triângulos têm os três lados correspondentes proporcionais, então
os triângulos são semelhantes.
A partir dos valores que já temos, vamos achar o valor de x:
x + 20o = 180o → x = 160o
7.
EXERCÍCIOS SOBRE TRIÂNGULOS
01 - As medidas dos ângulos de um triângulo são, respectivamente, x, 3x e 5x. Calcule o
valor de x.
2) Calcule o valor de x nas figuras:
Observa as figuras e determina o valor de x, em cada caso.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 15
Indica o valor das letras para cada um dos casos, justificando a resposta:
b)
Sendo a,b e c as medidas dos comprimentos dos lados de um triângulo, indica,
justificando, aqueles que são rectângulos:
a) a = 6; b = 7 e c = 13;
b) a = 6; b = 10 e c = 8.
Resolução:
"Se num triângulo as medidas dos seus lados verificarem o Teorema de Pitágoras então
pode-se concluir que o triângulo é rectângulo".
Então teremos que verificar para cada alínea se as medidas dos lados dos triângulos
satisfazem ou não o Teorema de Pitágoras.
a)
Resolução:
a) Aplicando o Teorema de Pitágoras temos:
logo o triângulo não é rectângulo porque não satisfaz o Teorema de Pitágoras.
b)
b) Aplicando o Teorema de Pitágoras temos:
logo o triângulo é rectângulo porque satisfaz o Teorema de Pitágoras.
Calcula o valor de x em cada um dos triângulos rectângulos:
a)
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 16
Calcula as áreas das seguintes figuras.
a)
b)
b)
Resolução:
a)
a) Qual era a altura do poste?
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 17
Resolução:
Resposta: A distância percorrida pelo berlinde é de:
265 cm = 2,65 m.
O Pedro e o João estão a «andar» de balancé, como indica a figura:
Resolução:
h=4+5=9
Resposta: A altura do poste era de 9 m.
b) Qual é a distância percorrida pelo berlinde.
A altura máxima a que pode subir cada um dos amigos é de 60 cm.
Qual o comprimento do balancé?
Resolução:
Pode-se aplicar o Teorema de Pitágoras, pois a linha a tracejado forma um ângulo de 90
graus com a "linha" do chão.
Então vem:
1,8 m = 180 cm
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 18
Resposta: O comprimento do balancé é de aproximadamente 190 cm, isto é, 1,9 m.
A figura representa um barco à vela.
6.1.) Determina, de acordo com os dados da figura, os valores de x e y.
Resolução:
6.1.) Aplicando o Teorema de Pitágoras, temos:
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 19
6. QUADRILÁTEROS E A SUA CLASSIFICAÇÃO
Quadrilátero é um polígono com
quatro lados e os principais
quadriláteros
são:
quadrado,
retângulo, losango, trapézio e
trapezóide.
No quadrilátero acima, observamos
alguns elementos geométricos:
1. Os vértices são os pontos: A,
B, C e D.
2. Os ângulos internos são A, B,
C e D.
3. Os lados são os segmentos
AB, BC, CD e DA.
Observação: Ao unir os vértices
opostos de um quadrilátero qualquer,
obtemos sempre dois triângulos e
como a soma das medidas dos
ângulos internos de um triângulo é
180 graus, concluímos que a soma
dos ângulos internos de um
quadrilátero é igual a 360 graus.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 20
Classificação dos Quadriláteros
Exercício: Determinar a medida do
ângulo x na gravura abaixo.
Paralelogramo: É o quadrilátero que
tem lados opostos paralelos. Num
paralelogramo, os ângulos opostos
são congruentes. Os paralelogramos
mais importantes recebem nomes
especiais:
1. Losango: 4 lados congruentes
2. Retângulo: 4 ângulos retos (90
graus)
3. Quadrado: 4 lados congruentes
e 4 ângulos retos.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 21
Alguns elementos gráficos de um
trapézio (parecido com aquele de um
circo).
Trapézio: É o quadrilátero que tem
apenas dois lados opostos paralelos.
1.
2.
3.
4.
AB é paralelo a CD
BC é não é paralelo a AD
AB é a base maior
DC é a base menor
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 22
Os trapézios recebem nomes de
acordo com os triângulos que têm
características semelhantes. Um
trapézio pode ser:
1. Retângulo: dois ângulos retos
2. Isósceles: lados não paralelos
congruentes
3. Escaleno: lados não paralelos
diferentes
Exercício:
Prolongar
as
retas
apoiadas nos lados opostos não
paralelos dos trapézios da figura
acima para obter, respectivamente,
um triângulo retângulo, um isósceles
e um escaleno. Observar mais acima
nesta mesma página os nomes dos
triângulos obtidos e os nomes destes
trapézios!
Triângulo e região triangular
No desenho abaixo, o triângulo ABC é a
reunião dos segmentos de reta AB, BC e
AC. A reunião de todos os pontos
localizados no triângulo e também dentro do
triângulo é chamada uma região triangular.
A região triangular ABC é limitada pelo
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 23
triângulo ABC. Os pontos dos lados do
triângulo ABC bem como os pontos do
interior do triângulo ABC são pontos da
região triangular.
Triângulo ABC
Região
triangular ABC
O conceito de região poligonal
Duas ou mais regiões triangulares não são
sobrepostas, se a interseção é vazia, é um
ponto ou é um segmento de reta. Cada uma
das regiões planas abaixo é a reunião de
três regiões triangulares não sobrepostas.
Uma região poligonal é a reunião de um
número finito de regiões triangulares nãosobrepostas e coplanares (estão no mesmo
plano). Na gravura abaixo, apresentamos
quatro regiões poligonais. Observe que uma
região triangular é por si mesmo uma região
poligonal e além disso uma região poligonal
pode conter "buracos".
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 24
Duas ou mais regiões poligonais são nãosobrepostas quando a interseção de duas
regiões quaisquer, é vazia, é um conjunto
finito de pontos, é um segmento de reta ou é
um conjunto finito de pontos e um segmento
de reta.
Uma região poligonal pode ser decomposta
em várias regiões triangulares e isto pode
ser feito de várias maneiras
O estudo de área de regiões poligonais
depende de alguns conceitos primitivos:
1. A cada região poligonal corresponde
um único número real positivo chamado
área.
2. Se dois triângulos são congruentes
então as regiões limitadas por eles
possuem a mesma área.
3. Se uma região poligonal é a reunião de
n regiões poligonais não-sobrepostas
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 25
então sua área é a soma das áreas das
n-regiões.
decomposição da região poligonal em
regiões triangulares.
Observação: Para facilitar o estudo de
regiões poligonais, adotaremos as seguintes
práticas:
a. Os desenhos de regiões poligonais
serão sombreadas apenas quando
houver possibilidade de confusão entre
o polígono e a região.
b. Usaremos expressões como a área do
triângulo ABC e a área do retângulo
RSTU no lugar de expressões como a
área da região triangular ABC e a área
da região limitada pelo retângulo RSTU.
Exemplo: A área da figura poligonal
ABCDEFX pode ser obtida pela
Após isto, realizamos as somas dessas
áreas triangulares.
Área(ABCDEFX)=área(XAB)+área(XB
C)+...+área(XEF)
Unidade de área
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 26
Para a unidade de medida de área,
traçamos um quadrado cujo lado tem uma
unidade de comprimento.
segmentos verticais, dividem o retângulo em
seis quadrados tendo cada um 1 unidade de
área.
Esta unidade pode ser o metro, o
centímetro, o quilômetro, etc.
Área do Retângulo
A figura ao lado mostra o retângulo ABCD,
que mede 3 unidades de comprimento e 2
unidades de altura. O segmento horizontal
que passa no meio do retângulo e os
A área do retângulo ABCD é a soma das
áreas destes seis quadrados. O número de
unidades de área do retângulo coincide com
o obtido pelo produto do número de
unidades do comprimento da base AB pelo
número de unidades da altura BC.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 27
O lado do retângulo pode ser visto como a
base e o lado adjacente como a altura,
assim, a área A do retângulo é o produto da
medida da base b pela medida da altura h.
A=b×h
A = x²
Exemplo: Obter a área do retângulo cujo
comprimento da base é 8 unidades e o
comprimento da altura é 5 unidades.
A = b×h
Área do quadrado
Um quadrado é um caso particular de
retângulo cuja medida da base é igual à
medida da altura. A área do quadrado pode
ser obtida pelo produto da medida da base
por si mesma.
Esta é a razão pela qual a segunda potência
do número x, indicada por x², tem o nome de
quadrado de x e a área A do quadrado é
obtida pelo quadrado da medida do lado x.
A = (8u)x(5u) = 40u²
No cálculo de áreas em situações reais,
usamos medidas de comprimento em
função de alguma certa unidade como:
metro, centímetro, quilômetro, etc...
Exemplo: Para calcular a área de um
retângulo com 2 m de altura e 120 cm de
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 28
base, podemos expressar a área em metros
quadrados ou qualquer outra unidade de
área.
1. Transformando as medidas em metros
Como h=2m e b=120cm=1,20m, a área
será obtida através de:
A = (1,20m)×(2m) =
2,40m²
as
medidas
A = (120cm)×(200cm) =
24000cm²
Área do Paralelogramo
Combinando os processos para obtenção de
áreas de triângulos congruentes com
aqueles de áreas de retângulos podemos
obter a área do paralelogramo.
A = b×h
2. Transformando
centímetros
A = b×h
em
Como h=2m=200cm e b=120cm, a área
do retângulo será dada por:
Qualquer lado do paralelogramo pode ser
tomado como sua base e a altura
correspondente é o segmento perpendicular
à reta que contém a base até o ponto onde
esta reta intercepta o lado oposto do
paralelogramo.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 29
No paralelogramo ABCD abaixo à esquerda,
os segmentos verticais tracejados são
congruentes e qualquer um deles pode
representar a altura do paralelogramo em
relação à base AB.
No paralelogramo RSTV acima à direita, os
dois segmentos tracejados são congruentes
e qualquer um deles pode representar a
altura do paralelogramo em relação à base
RV.
A área A do paralelogramo é obtida pelo
produto da medida da base b pela medida
da altura h, isto é, A=b×h. Demonstração da
fórmula
Área do Triângulo
A área de um triângulo é a metade do
produto da medida da base pela medida da
altura, isto é, A=b.h/2. Demonstração da
fórmula
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 30
Exemplo: Mostraremos que a área do
triângulo equilátero cujo lado mede s é dada
por A=s²R[3]/2, onde R[z] denota a raiz
quadrada de z>0. Realmente, com o
Teorema de Pitágoras, escrevemos h²=s²(s/2)² para obter h²=(3/4)s² garantindo que
h=R[3]s/2.
Como a área de um triângulo é dada por
A=b.h/2, então segue que:
A = s × R[3] s/2 = ½ R[3] s²
Observação: Triângulos com bases
congruentes e alturas congruentes possuem
a mesma área.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 31
Comparação de áreas entre triângulos semelhantes
Conhecendo-se a razão entre medidas
correspondentes quaisquer de dois
triângulos semelhantes, é possível obter a
razão entre as áreas desses triângulos.
Propriedade: A razão entre as áreas de dois
triângulos semelhantes é igual ao quadrado
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 32
da razão entre os comprimentos de
quaisquer dois lados correspondentes.
Área de
ABC
a²
=
Área de
RST
b²
=
r²
c²
=
s²
t²
A área do losango é o semi-produto das
medidas das diagonais, isto é, A=(d1×d2)/2.
Demonstração da fórmula
Área do losango
O losango é um paralelogramo e a sua área
é também igual ao produto do comprimento
da medida da base pela medida da altura.
Área do trapézio
Em um trapézio existe uma base menor de
medida b1, uma base maior de medida b2 e
uma altura com medida h.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 33
A área A do trapézio é o produto da média
aritmética entre as medidas das bases pela
medida da altura, isto é, A=(b1+b2).h/2.
Polígonos regulares
Um polígono regular é aquele que possui
todos os lados congruentes e todos os
ângulos congruentes. Existem duas
circunferências associadas a um polígono
regular.
Circunferência circunscrita: Em um polígono
regular com n lados, podemos construir uma
circunferência circunscrita (por fora), que é
uma circunferência que passa em todos os
vértices do polígono e que contém o
polígono em seu interior.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 34
Circunferência inscrita: Em um polígono
regular com n lados, podemos colocar uma
circunferência inscrita (por dentro), isto é,
uma circunferência que passa tangenciando
todos os lados do polígono e que está
contida no polígono.
4. Ângulo central é o ângulo cujo vértice é
o centro do polígono e cujos lados
contém vértices consecutivos do
polígono.
Elementos de um polígono regular
1. Centro do polígono é o centro comum
às
circunferências
inscrita
e
circunscrita.
2. Raio da circunferência circunscrita é a
distância do centro do polígono até um
dos vértices.
3. Raio da circunferência inscrita
é
o
apótema do polígono, isto é, a distância
do centro do polígono ao ponto médio
de um dos lados.
Apótema:
OM,
Raios: OA,OF
Ângulo
central: AOF
Apótema: OX,
Raios: OR,OT
Ângulo
central: ROT
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 35
5. Medida do ângulo central
de
um
polígono com n lados é dada por 360/n
graus. Por exemplo, o ângulo central de
um hexágono regular mede 60 graus e
o ângulo central de um pentágono
regular mede 360/5=72 graus.
Áreas de polígonos regulares
Traçando segmentos de reta ligando o
centro do polígono regular a cada um dos
vértices desse polígono de n-lados, iremos
decompor este polígono em n triângulos
congruentes.
Assim, a fórmula para o cálculo da área da
região poligonal regular será dada pela
metade do produto da medida do apótema a
pelo perímetro P, isto é:
A = a × Perímetro / 2
Demonstração da fórmula
Comparando áreas entre polígonos semelhantes
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 36
Apresentamos abaixo dois pentágonos
irregulares semelhantes. Dos vértices
correspondentes A e L traçamos diagonais
decompondo cada pentágono em três
triângulos.
Os pares de triângulos correspondentes
ABC e LMN, parecem semelhantes, o que
pode ser verificado diretamente através da
medição de seus ângulos com um
transferidor. Assumiremos que tal
propriedade seja válida para polígonos
semelhantes com n lados.
Observação: Se dois polígonos são
semelhantes, eles podem ser decompostos
no mesmo número de triângulos e cada
triângulo é semelhante ao triângulo que
ocupa a posição correspondente no outro
polígono.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 37
da razão entre os comprimentos de
quaisquer dois lados correspondentes.
Área de
ABCDE...
s²
=
Área de
A'B'C'D'E'...
Este fato e o teorema sobre razão entre
áreas de triângulos semelhantes são usados
para demonstrar o seguinte teorema sobre
áreas de polígonos semelhantes.
Teorema: A razão entre áreas de dois
polígonos semelhantes é igual ao quadrado
t²
=
(s')²
(t')²
Círculo, Circunferência e Arcos
A importância da circunferência
A
circunferência
possui
características
não
comumente
encontradas em outras figuras
planas, como o fato de ser a única
figura plana que pode ser rodada em
torno de um ponto sem modificar sua
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 38
posição aparente. É também a única
figura que é simétrica em relação a
um número infinito de eixos de
simetria.
A
circunferência
é
importante em praticamente todas as
áreas do conhecimento como nas
Engenharias, Matemática, Física,
Quimica,
Biologia,
Arquitetura,
Astronomia, Artes e também é muito
utilizado na indústria e bastante
utilizada
nas
residências
das
pessoas.
Circunferência e Círculo
Circunferência: A circunferência é o
lugar geométrico de todos os pontos
de um plano que estão localizados a
uma mesma distância r de um ponto
fixo denominado o centro da
circunferência. Esta talvez seja a
curva mais importante no contexto
das aplicações.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 39
Círculo: (ou disco) é o conjunto de
todos os pontos de um plano cuja
distância a um ponto fixo O é menor
ou igual que uma distância r dada.
Quando a distância é nula, o círculo
se reduz a um ponto. O círculo é a
reunião da circunferência com o
conjunto de pontos localizados
dentro da mesma. No gráfico acima,
a circunferência é a linha de cor
verde-escuro que envolve a região
verde, enquanto o círculo é toda a
região pintada de verde reunida com
a circunferência.
Pontos interiores de um círculo e exteriores a um círculo
Pontos
interiores:
Os
pontos
interiores de um círculo são os
pontos do círculo que não estão na
circunferência.
Pontos
exteriores:
Os
pontos
exteriores a um círculo são os
pontos localizados fora do círculo.
Raio, corda e diâmetro
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 40
Raio: Raio de uma circunferência (ou
de um círculo) é um segmento de
reta com uma extremidade no centro
da circunferência e a outra
extremidade num ponto qualquer da
circunferência.
Na
figura,
os
segmentos de reta OA, OB e OC são
raios.
Corda: Corda de uma circunferência
é um segmento de reta cujas
extremidades
pertencem
à
circunferência.
Na
figura,
os
segmentos de reta AC e DE são
cordas.
Diâmetro:
Diâmetro
de
uma
circunferência (ou de um círculo) é
uma corda que passa pelo centro da
circunferência. Observamos que o
diâmetro é a maior corda da
circunferência.
Na
figura,
o
segmento de reta AC é um diâmetro.
Posições relativas de uma reta e uma circunferência
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 41
Reta secante: Uma reta é secante a
uma circunferência se essa reta
intercepta a circunferência em dois
pontos quaisquer, podemos dizer
também que é a reta que contém
uma corda.
único ponto P. Este ponto é
conhecido como ponto de tangência
ou ponto de contato. Na figura ao
lado, o ponto P é o ponto de
tangência e a reta que passa pelos
pontos E e F é uma reta tangente à
circunferência.
Observações:
Reta tangente: Uma reta tangente a
uma circunferência é uma reta que
intercepta a circunferência em um
1. Raios e diâmetros são nomes
de segmentos de retas mas às
vezes são também usados
como os comprimentos desses
segmentos.
Por
exemplo,
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 42
podemos dizer que ON é o raio
da circunferência, mas é usual
dizer que o raio ON da
circunferência mede 10cm ou
que o raio ON tem 10cm.
2. Tangentes e secantes são
nomes de retas, mas também
são usados para denotar
segmentos de retas ou semiretas.
Por
exemplo,
"A
tangente PQ" pode significar a
reta tangente à circunferência
que passa pelos pontos P e Q
mas também pode ser o
segmento de reta tangente à
circunferência que liga os
pontos P e Q. Do mesmo
modo, a "secante AC" pode
significar a reta que contém a
corda BC e também pode ser o
segmento de reta ligando o
ponto A ao ponto C.
Propriedades das secantes e tangentes
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 43
1. Se uma reta s,
secante a uma
circunferência de
centro
O,
intercepta
a
circunferência
em dois pontos distintos A e B
e se M é o ponto médio da
corda AB, então o segmento de
reta OM é perpendicular à reta
secante s.
2. Se uma reta s, secante a uma
circunferência de centro O,
intercepta a circunferência em
dois pontos distintos A e B, a
perpendicular à reta s que
passa pelo centro O da
circunferência, passa também
pelo ponto médio da corda AB.
3. Seja OP um raio
de
uma
circunferência,
onde O é o
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 44
centro e P um ponto da
circunferência.
Toda
reta
perpendicular ao raio OP é
tangente à circunferência no
ponto de tangência P.
Reta tangente comum: Uma reta que
é tangente a duas circunferências ao
mesmo tempo é denominada uma
tangente comum. Há duas possíveis
retas tangentes comuns: a interna e
a externa.
Tangente comum interna
Tangente comum ext
4. Toda reta tangente a uma
circunferência é perpendicular
ao raio no ponto de tangência.
Posições relativas de duas circunferências
Ao traçar uma reta ligando os
centros de duas circunferências no
plano, esta reta separa o plano em
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 45
dois semi-planos. Se os pontos de
tangência,
um
em
cada
circunferência, estão no mesmo
semi-plano, temos uma reta tangente
comum externa. Se os pontos de
tangência,
um
em
cada
circunferência, estão em semi-planos
diferentes, temos uma reta tangente
comum interna.
Circunferências
internas:
Uma
circunferência C1 é interna a uma
circunferência C2, se todos os
pontos do círculo C1 estão contidos
no círculo C2. Uma circunferência é
externa à outra se todos os seus
pontos são pontos externos à outra.
Circunferências concêntricas: Duas
ou mais circunferências com o
mesmo centro mas com raios
diferentes
são
circunferências
concêntricas.
Circunferências tangentes: Duas
circunferências que estão no mesmo
plano, são tangentes uma à outra, se
elas são tangentes à mesma reta no
mesmo ponto de tangência.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 46
nf. tangentes externas
Circunferências
secantes:
são
Circunf. tangentes internas
aquelas que possuem somente dois
pontos distintos em comum.
As circunferências são tangentes
externas uma à outra se os seus
centros estão em lados opostos da
reta tangente comum e elas são
tangentes internas uma à outra se os
seus centros estão do mesmo lado
da reta tangente comum.
Segmentos tangentes: Se AP e BP
são segmentos de reta tangentes à
circunferência nos ponto A e B,
então esses segmentos AP e BP são
congruentes.
Polígonos circunscritos
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 47
Polígono
circunscrito
a
uma
circunferência é o que possui seus
lados tangentes à circunferência. Ao
mesmo tempo, dizemos que esta
circunferência está inscrita no
polígono.
adrilátero circunscrito
circunscrito a uma circunferência, a
soma de dois lados opostos é igual a
soma dos outros dois lados.
Arco de circunferência e ângulo central
Seja a circunferência de
Triângulo circunscrito
centro O traçada ao lado.
Pela
definição
de
circunferência temos que
OP=OQ=OR=... e isto indica que os
raios de uma circunferência são
segmentos congruentes.
Propriedade
dos
quadriláteros
circunscritos: Se um quadrilátero é
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 48
Circunferências congruentes: São
circunferências que possuem raios
congruentes. Aqui a palavra raio
refere-se ao segmento de reta e não
a um número.
Ângulo central: Em uma
circunferência, o ângulo
central é aquele cujo
vértice coincide com o centro da
circunferência. Na figura, o ângulo a
é um ângulo central. Se numa
circunferência de centro O, um
ângulo central determina um arco
AB, dizemos que AB é o arco
correspondente ao ângulo AÔB.
Arco menor: É um arco que reúne
dois pontos da circunferência que
não são extremos de um diâmetro e
todos os pontos da circunferência
que estão dentro do ângulo central
cujos lados contém os dois pontos.
Na figura, a linha vermelha indica o
arco menor AB ou arco menor ACB.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 49
Arco maior: É
um arco que liga
dois pontos da
circunferência
que não são
extremos de um diâmetro e todos os
pontos da circunferência que estão
fora do ângulo central cujos lados
contém os dois pontos. Na figura a
parte azul é o arco maior, o ponto D
está no arco maior ADB enquanto o
ponto C não está no arco maior mas
está no arco menor AB, assim é
frequentemente usado três letras
para representar o arco maior.
Semicircunferência: É um
arco obtido pela reunião
dos pontos extremos de
um diâmetro com todos os
pontos da circunferência
que estão em um dos lados do
diâmetro. O arco RTS é uma
semicircunferência da circunferência
de centro P e o arco RUS é outra.
Observações:
Em
uma
circunferência dada, temos que:
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 50
1. A medida
do
arco
menor é a
medida do
ângulo central correspondente
a m(AÔB) e a medida do arco
maior é 360 graus menos a
medida
do
arco
menor
m(AÔB).
2.
3. A
medida
da
semicircunferência é 180 graus
ou Pi radianos.
4. Em
circunferências
congruentes ou em uma
simples circunferência, arcos
que possuem medidas iguais
são arcos congruentes.
5. Em
uma
circunferência,
se
um ponto E está
entre os pontos D e
F, que são extremidades de um
arco
menor,
então:
m(DE)+m(EF)=m(DF).
6.
7. Se o ponto E está
entre os pontos D e
F, extremidades de
um arco maior:
m(DE)+m(EF)=m(DEF).
8.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 51
Apenas esta última relação faz
sentido para as duas últimas
figuras apresentadas.
Propriedades de arcos e cordas
Uma corda de uma
circunferência é um
segmento de reta que
une dois pontos da
circunferência. Se os
extremos de uma corda não são
extremos de um diâmetro eles são
extremos de dois arcos de
circunferência sendo um deles um
arco menor e o outro um arco maior.
Quando não for especificada, a
expressão arco de uma corda se
referirá ao arco menor e quanto ao
arco maior sempre teremos que
especificar.
Observações
1. Se um ponto X está em um
arco AB e o arco AX é
congruente ao arco XB, o ponto
X é o ponto médio do arco AB.
Além disso, qualquer segmento
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 52
de reta que contém o ponto X é
um segmento bissetor do arco
AB. O ponto médio do arco não
é o centro do arco, o centro do
arco
é
o
centro
da
circunferência que contém o
arco.
2. Para
obter
a
distância de um
ponto O a uma reta
r, traçamos uma
reta perpendicular
à reta dada passando pelo
ponto O. O ponto T obtido pela
interseção dessas duas retas é
o ponto que determinará um
extremo do segmento OT cuja
medida representa a distância
entre o ponto e a reta.
3.
4. Em uma mesma circunferência
ou
em
circunferências
congruentes,
cordas
congruentes possuem arcos
congruentes
e
arcos
congruentes possuem cordas
congruentes. (Situação 1).
5. Um
diâmetro
que
é
perpendicular a uma corda é
bissetor da corda e também de
seus dois arcos. (Situação 2).
6. Em uma mesma circunferência
ou
em
circunferências
congruentes,
cordas
que
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 53
possuem a mesma distância do
centro
são
congruentes.
(Situação 3).
uação 1
Situação 2
que a circunferência é circunscrita ao
polígono.
Situação 3
Polígonos inscritos na circunferência
Um polígono é inscrito em uma
circunferência se cada vértice do
polígono
é
um
ponto
da
circunferência e neste caso dizemos
Propriedade
dos
quadriláteros
inscritos: Se um quadrilátero está
inscrito em uma circunferência então
os
ângulos
opostos
são
suplementares, isto é a soma dos
ângulos opostos é 180 graus e a
soma de todos os quatro ângulos é
360 graus.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 54
 + Π= 180 graus
Ê + Ô = 180 graus
 + Ê + Î + Ô = 360 graus
Ângulos inscritos
Ângulo inscrito: relativo a uma
circunferência é um ângulo com o
vértice na circunferência e os lados
secantes a ela. Na figura à esquerda
abaixo, o ângulo AVB é inscrito e AB
é o arco correspondente.
Medida do ângulo inscrito: A medida
de um ângulo inscrito em uma
circunferência é igual à metade da
respectiva medida do ângulo central,
ou seja, a metade de seu arco
correspondente, isto é:
m = n/2 = (1/2) m(AB)
Ângulo reto inscrito na
circunferência: O arco
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 55
correspondente a um ângulo reto
inscrito em uma circunferência é a
semi-circunferência. Se um triângulo
inscrito numa semi-circunferência
tem um lado igual ao diâmetro, então
ele é um triângulo retângulo e esse
diâmetro é a hipotenusa do triângulo.
ângulo determina um arco (menor)
sobre a circunferência. No gráfico ao
lado, a reta secante passa pelos
pontos A e B e o arco
correspondente ao ângulo semiinscrito BAC é o arco AXB onde X é
um ponto sobre o arco.
Ângulo semi-inscrito e arco capaz
Ângulo semi-inscrito: Ângulo semiinscrito ou ângulo de segmento é um
ângulo que possui um dos lados
tangente à circunferência, o outro
lado secante à circunferência e o
vértice na circunferência. Este
Observação: A medida do ângulo
semi-inscrito é a metade da medida
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 56
do arco interceptado. Na figura, a
medida do ângulo BÂC é igual a
metade da medida do arco AXB.
Arco
capaz:
Dado
um
segmento AB e
um ângulo k,
pergunta-se:
Qual é o lugar
geométrico de todos os pontos do
plano que contém os vértices dos
ângulos cujos lados passam pelos
pontos A e B sendo todos os ângulos
congruentes ao ângulo k? Este lugar
geométrico
é
um
arco
de
circunferência denominado arco
capaz.
Construção do arco capaz com
régua e compasso:
1. Traçar um segmento de reta
AB;
2. Pelo ponto A, trace uma reta t
formando com o segmento AB
um ângulo congruente a k
(mesma medida que o ângulo
k);
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 57
3. Traçar
uma
reta
p
perpendicular à reta t passando
pelo ponto A;
4. Determinar o ponto médio M do
segmento AB;
5. Traçar a reta mediatriz m ao
segmento AB;
6. Obter o ponto O que é a
interseção entre a reta p e a
mediatriz m.
7. Com o compasso centrado no
ponto O e abertura OA, traçar o
arco
de
circunferência
localizado acima do segmento
AB.
8. O arco que aparece em
vermelho no gráfico ao lado é o
arco capaz.
Observação: Todo ângulo inscrito no
arco capaz AB, com lados passando
pelos pontos A e B são congruentes
e isto significa que, o segmento de
reta AB é sempre visto sob o mesmo
ângulo de visão se o vértice deste
ângulo está localizado no arco
capaz. Na figura abaixo à esquerda,
os ângulos que passam por A e B e
têm vértices em V1, V2, V3, ..., são
todos congruentes (a mesma
medida).
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 58
Na figura acima à direita, o arco
capaz relativo ao ângulo semiinscrito m de vértice em A é o arco
AVB. Se n é ângulo central então a
medida de m é o dobro da medida
de n, isto é:
m(arco AB) = 2 medida(m) =
medida(n)
Outras propriedades com cordas e segmentos
Agora
apresentaremos
alguns resultados que
fazem a conexão
entre segmentos e
cordas, que não são
evidentes à primeira vista. Se a reta
AB é tangente à circunferência no
ponto B então o segmento AB é o
segmento tangente de A até a
circunferência. Se a reta RT é uma
reta secante que intercepta a
circunferência em S e T e R é um
ponto exterior a circunferência, então
RT é um segmento secante e RS é a
parte externa do segmento secante.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 59
Na sequência, usaremos a notação
(PZ) para representar a medida do
segmento PZ, em função das
dificuldades que a linguagem HTML
proporciona para a apresentação de
materiais de Matemática.
Cordas interceptando
dentro
da
circunferência:
Se
duas cordas de uma
mesma
circunferência
interceptam em um ponto P dentro
da circunferência, então o produto
das medidas das duas partes de
uma corda é igual ao produto das
medidas das duas partes da outra
corda.
(AP).(PB) = (CP).(PD)
se
Potência de ponto (1): A partir de um
ponto fixo P dentro de uma
circunferência, tem-se que (PA).(PB)
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 60
é constante qualquer que seja a
corda AB passando por este ponto
P. Este produto (PA).(PB) é
denominado a potência do ponto P
em relação a esta
circunferência.
Secantes
interceptando fora
da circunferência:
Consideremos
duas
retas
secantes
a
uma
mesma
circunferência que se interceptam
em um ponto P localizado fora da
circunferência.
Se uma das retas passa pelos
pontos A e B e a outra reta passa
pelos
pontos
C
e
D
da
circunferência, então o produto da
medida do segmento secante PA
pela medida da sua parte exterior PB
é igual ao produto da medida do
segmento secante PC pela medida
da sua parte exterior PD.
(PA).(PB)=(PC).(PD)
Potência de ponto (2): Se P é um
ponto fixo fora da circunferência, o
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 61
produto (PA).(PB) é constante
qualquer que seja a reta secante à
circunferência passando por P. Este
produto
(PA).(PB)
é
também
denominado a potência do ponto P
em relação à circunferência.
Secante
e
tangente
interceptando
fora
da
circunferência:
Se uma reta secante e uma reta
tangente
a
uma
mesma
circunferência se interceptam em um
ponto P fora da circunferência, a reta
secante passando pelos pontos A e
B e a reta tangente passando pelo
ponto
T
de
tangência
à
circunferência, então o quadrado da
medida do segmento tangente PT é
igual ao produto da medida do
segmento secante PA pela medida
da sua parte exterior PB.
(PT)2 = (PA).(PB)
Exemplo:
Consideremos
a
figura ao lado com
as cordas AB e CD
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 62
tendo interseção no ponto P, com
(AP) = 5cm,
(PB) = 8cm,
(CD) = 14cm. Iremos obter a medida
do segmento PD. Tomaremos
(PD)=x, para podermos escrever que
(CP) = 14-x e somente utilizaremos a
unidade de medida no final. Desse
modo,
(PD).(PC)=(PA).(PB)
e
podemos escrever que x(14-x)=5×8,
de onde segue que x²-14x+40=0.
Resolvendo esta equação do
segundo grau, obtemos: x=4 ou
x=10, o que significa que se uma das
partes do segmento medir 4cm, a
outra medirá 10cm. Pela figura
anexada,
observamos
que
o
segmento PD é maior que o
segmento PC e concluímos que
(PD)=10cm e (PC)=4cm.
Áreas de regiões poligonais
Triângulo e região triangular
No desenho abaixo, o triângulo ABC é a
reunião dos segmentos de reta AB, BC e
AC. A reunião de todos os pontos
localizados no triângulo e também dentro do
triângulo é chamada uma região triangular.
A região triangular ABC é limitada pelo
triângulo ABC. Os pontos dos lados do
triângulo ABC bem como os pontos do
interior do triângulo ABC são pontos da
região triangular.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 63
Triângulo ABC
Região
triangular ABC
O conceito de região poligonal
Duas ou mais regiões triangulares não são
sobrepostas, se a interseção é vazia, é um
ponto ou é um segmento de reta. Cada uma
das regiões planas abaixo é a reunião de
três regiões triangulares não sobrepostas.
Uma região poligonal é a reunião de um
número finito de regiões triangulares nãosobrepostas e coplanares (estão no mesmo
plano). Na gravura abaixo, apresentamos
quatro regiões poligonais. Observe que uma
região triangular é por si mesmo uma região
poligonal e além disso uma região poligonal
pode conter "buracos".
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 64
Duas ou mais regiões poligonais são nãosobrepostas quando a interseção de duas
regiões quaisquer, é vazia, é um conjunto
finito de pontos, é um segmento de reta ou é
um conjunto finito de pontos e um segmento
de reta.
Uma região poligonal pode ser decomposta
em várias regiões triangulares e isto pode
ser feito de várias maneiras
O estudo de área de regiões poligonais
depende de alguns conceitos primitivos:
1. A cada região poligonal corresponde
um único número real positivo chamado
área.
2. Se dois triângulos são congruentes
então as regiões limitadas por eles
possuem a mesma área.
3. Se uma região poligonal é a reunião de
n regiões poligonais não-sobrepostas
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 65
então sua área é a soma das áreas das
n-regiões.
decomposição da região poligonal em
regiões triangulares.
Observação: Para facilitar o estudo de
regiões poligonais, adotaremos as seguintes
práticas:
a. Os desenhos de regiões poligonais
serão sombreadas apenas quando
houver possibilidade de confusão entre
o polígono e a região.
b. Usaremos expressões como a área do
triângulo ABC e a área do retângulo
RSTU no lugar de expressões como a
área da região triangular ABC e a área
da região limitada pelo retângulo RSTU.
Exemplo: A área da figura poligonal
ABCDEFX pode ser obtida pela
Após isto, realizamos as somas dessas
áreas triangulares.
Área(ABCDEFX)=área(XAB)+área(XB
C)+...+área(XEF)
Unidade de área
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 66
Para a unidade de medida de área,
traçamos um quadrado cujo lado tem uma
unidade de comprimento.
segmentos verticais, dividem o retângulo em
seis quadrados tendo cada um 1 unidade de
área.
Esta unidade pode ser o metro, o
centímetro, o quilômetro, etc.
Área do Retângulo
A figura ao lado mostra o retângulo ABCD,
que mede 3 unidades de comprimento e 2
unidades de altura. O segmento horizontal
que passa no meio do retângulo e os
A área do retângulo ABCD é a soma das
áreas destes seis quadrados. O número de
unidades de área do retângulo coincide com
o obtido pelo produto do número de
unidades do comprimento da base AB pelo
número de unidades da altura BC.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 67
O lado do retângulo pode ser visto como a
base e o lado adjacente como a altura,
assim, a área A do retângulo é o produto da
medida da base b pela medida da altura h.
A=b×h
A = x²
Exemplo: Obter a área do retângulo cujo
comprimento da base é 8 unidades e o
comprimento da altura é 5 unidades.
A = b×h
Área do quadrado
Um quadrado é um caso particular de
retângulo cuja medida da base é igual à
medida da altura. A área do quadrado pode
ser obtida pelo produto da medida da base
por si mesma.
Esta é a razão pela qual a segunda potência
do número x, indicada por x², tem o nome de
quadrado de x e a área A do quadrado é
obtida pelo quadrado da medida do lado x.
A = (8u)x(5u) = 40u²
No cálculo de áreas em situações reais,
usamos medidas de comprimento em
função de alguma certa unidade como:
metro, centímetro, quilômetro, etc...
Exemplo: Para calcular a área de um
retângulo com 2 m de altura e 120 cm de
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 68
base, podemos expressar a área em metros
quadrados ou qualquer outra unidade de
área.
1. Transformando as medidas em metros
Como h=2m e b=120cm=1,20m, a área
será obtida através de:
A = (1,20m)×(2m) =
2,40m²
as
medidas
A = (120cm)×(200cm) =
24000cm²
Área do Paralelogramo
Combinando os processos para obtenção de
áreas de triângulos congruentes com
aqueles de áreas de retângulos podemos
obter a área do paralelogramo.
A = b×h
2. Transformando
centímetros
A = b×h
em
Como h=2m=200cm e b=120cm, a área
do retângulo será dada por:
Qualquer lado do paralelogramo pode ser
tomado como sua base e a altura
correspondente é o segmento perpendicular
à reta que contém a base até o ponto onde
esta reta intercepta o lado oposto do
paralelogramo.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 69
No paralelogramo ABCD abaixo à esquerda,
os segmentos verticais tracejados são
congruentes e qualquer um deles pode
representar a altura do paralelogramo em
relação à base AB.
No paralelogramo RSTV acima à direita, os
dois segmentos tracejados são congruentes
e qualquer um deles pode representar a
altura do paralelogramo em relação à base
RV.
A área A do paralelogramo é obtida pelo
produto da medida da base b pela medida
da altura h, isto é, A=b×h. Demonstração da
fórmula
Área do Triângulo
A área de um triângulo é a metade do
produto da medida da base pela medida da
altura, isto é, A=b.h/2. Demonstração da
fórmula
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 70
Exemplo: Mostraremos que a área do
triângulo equilátero cujo lado mede s é dada
por A=s²R[3]/2, onde R[z] denota a raiz
quadrada de z>0. Realmente, com o
Teorema de Pitágoras, escrevemos h²=s²(s/2)² para obter h²=(3/4)s² garantindo que
h=R[3]s/2.
Como a área de um triângulo é dada por
A=b.h/2, então segue que:
A = s × R[3] s/2 = ½ R[3] s²
Observação: Triângulos com bases
congruentes e alturas congruentes possuem
a mesma área.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 71
Comparação de áreas entre triângulos semelhantes
Conhecendo-se a razão entre medidas
correspondentes quaisquer de dois
triângulos semelhantes, é possível obter a
razão entre as áreas desses triângulos.
Propriedade: A razão entre as áreas de dois
triângulos semelhantes é igual ao quadrado
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 72
da razão entre os comprimentos de
quaisquer dois lados correspondentes.
Área de
ABC
a²
=
Área de
RST
b²
=
r²
c²
=
s²
t²
A área do losango é o semi-produto das
medidas das diagonais, isto é, A=(d1×d2)/2.
Demonstração da fórmula
Área do losango
O losango é um paralelogramo e a sua área
é também igual ao produto do comprimento
da medida da base pela medida da altura.
Área do trapézio
Em um trapézio existe uma base menor de
medida b1, uma base maior de medida b2 e
uma altura com medida h.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 73
A área A do trapézio é o produto da média
aritmética entre as medidas das bases pela
medida da altura, isto é, A=(b1+b2).h/2.
Polígonos regulares
Um polígono regular é aquele que possui
todos os lados congruentes e todos os
ângulos congruentes. Existem duas
circunferências associadas a um polígono
regular.
Circunferência circunscrita: Em um polígono
regular com n lados, podemos construir uma
circunferência circunscrita (por fora), que é
uma circunferência que passa em todos os
vértices do polígono e que contém o
polígono em seu interior.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 74
Circunferência inscrita: Em um polígono
regular com n lados, podemos colocar uma
circunferência inscrita (por dentro), isto é,
uma circunferência que passa tangenciando
todos os lados do polígono e que está
contida no polígono.
4. Ângulo central é o ângulo cujo vértice é
o centro do polígono e cujos lados
contém vértices consecutivos do
polígono.
Elementos de um polígono regular
1. Centro do polígono é o centro comum
às
circunferências
inscrita
e
circunscrita.
2. Raio da circunferência circunscrita é a
distância do centro do polígono até um
dos vértices.
3. Raio da circunferência inscrita
é
o
apótema do polígono, isto é, a distância
do centro do polígono ao ponto médio
de um dos lados.
Apótema:
OM,
Raios: OA,OF
Ângulo
central: AOF
Apótema: OX,
Raios: OR,OT
Ângulo
central: ROT
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 75
5. Medida do ângulo central
de
um
polígono com n lados é dada por 360/n
graus. Por exemplo, o ângulo central de
um hexágono regular mede 60 graus e
o ângulo central de um pentágono
regular mede 360/5=72 graus.
Áreas de polígonos regulares
Traçando segmentos de reta ligando o
centro do polígono regular a cada um dos
vértices desse polígono de n-lados, iremos
decompor este polígono em n triângulos
congruentes.
Assim, a fórmula para o cálculo da área da
região poligonal regular será dada pela
metade do produto da medida do apótema a
pelo perímetro P, isto é:
A = a × Perímetro / 2
Demonstração da fórmula
Comparando áreas entre polígonos semelhantes
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 76
Apresentamos abaixo dois pentágonos
irregulares semelhantes. Dos vértices
correspondentes A e L traçamos diagonais
decompondo cada pentágono em três
triângulos.
Os pares de triângulos correspondentes
ABC e LMN, parecem semelhantes, o que
pode ser verificado diretamente através da
medição de seus ângulos com um
transferidor. Assumiremos que tal
propriedade seja válida para polígonos
semelhantes com n lados.
Observação: Se dois polígonos são
semelhantes, eles podem ser decompostos
no mesmo número de triângulos e cada
triângulo é semelhante ao triângulo que
ocupa a posição correspondente no outro
polígono.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 77
da razão entre os comprimentos de
quaisquer dois lados correspondentes.
Área de
ABCDE...
s²
=
Área de
A'B'C'D'E'...
Este fato e o teorema sobre razão entre
áreas de triângulos semelhantes são usados
para demonstrar o seguinte teorema sobre
áreas de polígonos semelhantes.
Teorema: A razão entre áreas de dois
polígonos semelhantes é igual ao quadrado
t²
=
(s')²
(t')²
Áreas de regiões circulares
O círculo como o limite de regiões poligonais regulares
Nas figuras abaixo, temos três regiões
poligonais regulares inscritas em círculos
congruentes.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 78
não podemos construir uma expressão
matemática para o cálculo do perímetro ou
da área de uma região poligonal regular
inscrita num círculo.
Quando aumenta o número de lados do
polígono inscrito observamos que també
aumenta:
1. O apótema, aproximando-se do raio do
cículo como um limite.
2. O perímetro, aproximando-se da
circunferência do círculo como um
limite.
3. A área, aproximando-se da área do
círculo como um limite.
Neste trabalho não é possível apresentar
uma definição precisa de limite e sem ela
A idéia de limite nos permite aproximar o
perímetro da circunferência pelo perímetro
do polígono regular inscrito nessa
circunferência, à medida que o número de
lados do polígono aumenta.
O mesmo ocorre com o cálculo da área do
círculo, pois à medida que o número de
lados da região poligonal inscrita aumenta,
as áreas dessas regiões se aproximam da
área do círculo. Este também é um processo
através de limites.
Perímetro do círculo e da circunferência
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 79
Perímetro da circunferência de um círculo é
o valor limite da sequência dos perímetros
dos polígonos regulares inscritos de n lados
na circunferência à medida que o número n
de lados aumenta indefinidamente.
Área do círculo é o valor limite da sequência
das áreas das regiões poligonais regulares
inscritas no círculo quando o número n de
lados das poligonais aumenta
arbitrariamente.
Relações associadas ao perímetro
1. Com base nestas duas definições
temos um importante resultado sobre a
relação existente entre o perímetro e o
diâmetro da circunferência:
A razão entre o perímetro e o
diâmetro
de uma circunferência é uma
constante
2. Sejam
duas
circunferências
de
diâmetros D1 e D2, com perímetros P1
e P2, respectivamente. A razão entre os
perímetros P1 e P2 é igual à razão
entre os diâmetros D1 e D2. Como o
diâmetro é o dobro do raio, então, o
mesmo ocorre para a razão entre os
raios r1 e r2.
A1
=
D1
=
r1
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 80
A2
D2
r2
inscritas no mesmo. Nesse caso, o diâmetro
D=2r. As fórmulas para a área do círculo
são:
3. Para
todo
círculo
(e
também
circunferência), a razão entre o
perímetro e o diâmetro é uma
constante, denominada Pi, denotada
pela letra grega
que é um número
irracional (não pode ser escrito como a
divisão de dois números inteiros). Uma
aproximação para Pi com 10 dígitos
decimais é:
Área =
D²
Proporção com áreas: Sejam dois círculos
de raios, respectivamente, iguais a r1 e r2,
áreas A1 e A2 e diâmetros D1 e D2. A razão
entre as áreas desses dois círculos é a
mesma que a razão entre os quadrados de
seus raios ou os quadrados de seus
diâmetros.
= 3,1415926536....
A1
(D1)²
=
Área do círculo
Área de um círculo de raio r é o limite das
áreas das regiões poligonais regulares
r² = ¼
A2
Arcos
(r1)²
=
(D2)²
(r2)²
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 81
O comprimento de um arco genérico AB
pode ser descrito em termos de um limite.
Imaginemos o arco AB contendo vários
pontos A=Po, P1, P2, P3, ..., Pn-1, Pn=B,
formando n pequenos arcos e também n
pequenos segmentos de reta de medidas
respectivas iguais a: AP1, P1P2, ..., Pn-1B.
pequeno e as medidas dos arcos sejam
aproximadamente iguais às medidas dos
segmentos.
O comprimento de um arco AB de uma
circunferência de raio r é o valor limite da
soma dos comprimentos destas n cordas
quando n cresce indefinidamente.
Um arco completo de circunferência
corresponde a um ângulo que mede 360
graus=2 radianos. Se o raio da
circunferência for r, o perímetro da
circunferência coincidirá com o comprimento
do arco da mesma e é dado por:
Perímetro da circunferência = 2 r
A idéia aqui é tomar um número n bastante
grande para que cada segmento seja
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 82
Comprimento do arco: Seja um arco AB em
uma circunferência de raio r e
m a medida do ângulo
correspondente, sendo m
tomado em graus ou em
radianos. O comprimento do
arco pode ser obtido (em
radianos) por:
360 graus ……… 2 Pi r
m
AB
graus ……… Comprimento de
logo
comprimento do arco AB = m r
Comprimento do arco AB =
=rm
r m/180
Tais fórmulas podem ser justificadas pelas
seguintes regras de três simples e diretas.
Se o ângulo relativo ao arco AB mede m
graus, obtemos:
/ 180
Se o ângulo relativo ao arco AB mede m
radianos, obtemos:
2 Pi rad ……… 2 Pi r
m
AB
assim
rad ……… comprimento de
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 83
Comprimento do arco AB = r m
radianos
Setor circular
Setor circular é uma região limitada por dois
raios e um arco do círculo.
3.
4.
5.
6.
r é o raio de cada um dos setores
ACB é o arco do setor OACB
ADB é o arco do setor OADB.
Tomando m como a medida do arco
ACB (em graus ou radianos), a área do
setor circular OACB será dada por:
Área do setor circular OACB =
m/360 = ½ m r²
r²
Basta usar regras de três simples e diretas.
Se o ângulo relativo ao arco AB mede m
graus, obtemos:
Usando a figura acima, podemos extrair
algumas informações:
1. OACB é um setor circular
2. OADB é um setor circular
360 graus ……… Área do
círculo
m
graus ……… Área do setor
OACB
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 84
logo
abaixo, existem dois segmentos circulares: o
segmento ACB e o segmento ADB.
Área(setor OACB) = Pi r² m / 360
Se o ângulo relativo ao arco AB mede m
radianos, obtemos:
2 Pi rad ……… Área do círculo
m
rad ……… Área setor OACB
assim
Área(setor OACB) = ½ m r² radianos
Segmento circular
Segmento circular é uma região limitada por
uma corda e um arco do círculo. Na figura
A área do segmento ACB pode ser obtida
subtraindo a área do triângulo AOB da área
do setor OACB.
Área(segmento) = Área(setor OACB) Área(triângulo AOB)
A área do segmento ADB pode ser obtida
subtraindo a área do segmento ACB da área
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 85
do círculo ou somando a área do triângulo
AOB à área do setor OADB.
3. e media dez côvados
duma borda à outra,
cinco
4. côvados de altura e
trinta de
circunferência."
Curiosidades sobre o número Pi
1. Na Bíblia Sagrada, no primeiro livro de
Reis 7:23, existe a passagem:
2. "Fez também o mar de
fundição; era redondo
sugerindo que os construtores da casa
de Salomão usavam o valor 3 para a
razão entre o diâmetro e o comprimento
da circunferência.
5. Arquimedes (287-212 a.C.) mostrou
que o valor da razão entre o diâmetro e
o comprimento da circunferência estava
entre 3+1/7 e 3+10/71.
6. O símbolo usado para a razão entre o
diâmetro e o comprimento da
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 86
circunferência somente foi introduzido
no século XVIII.
7. O valor de
correto com 10 dígitos
decimais foi usado no cálculo do
comprimento da linha do Equador
terrestre.
8. Uma vez conhecida uma unidade de
comprimento, é impossível construir um
segmento de comprimento Pi através
de régua e compasso.
9. O número
exerce um papel muito
importante na Matemática e nas
ciências, predominantemente quando
determinamos
perímetros,
áreas,
centros de gravidade, informações
sobre segmentos e setores circulares e
elípticos, inclusive em cálculos de
navegação, etc.
10. Com o uso de computadores, já foi
realizado o cálculo do valor exato de
com mais de cem mil dígitos decimais.
Detalhes sobre o cálculo de Pi: De modo
análogo ao resultado obtido através do limite
de polígonos regulares inscritos também
podemos aproximar o perímetro e a área do
círculo de raio r, pelo valor limite de
polígonos regulares circunscritos no círculo
quando o número de lados desse cresce
arbitrariamente.
Perímetro
polígono
inscrito
2r
<
<
Perímetro
polígono
circunscrito
2r
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 87
Tais relações estão na tabela com dados
sobre o polígono regular dado:
Número
de lados
do
polígono
6
12
24
48
96
192
Perímetro
do
polígono
inscrito
dividido
por 2r
3,00000
3,10582
3,13262
3,13935
3,14103
3,14145
256
512
1024
3,14151
3,14157
3,14159
3,14175
3,14163
3,14160
Perímetro
do polígono
circunscrito
dividido por
2r
Observe na tabela que quanto maior o
número de lados de cada polígono mais
dígitos decimais coincidem para obter o
valor do número Pi, tanto para os polígonos
inscritos como para os circunscritos. Com
um polígono de 1024 lados, praticamente
temos 4 algarismos exatos.
3,46411
3,21540
3,15967
3,14609
3,14272
3,14188
Outra forma (lenta) para obter o número Pi,
é:
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 88
A forma mais rápida que conhecemos para
obter Pi, é:
obtida em The miraculous Bailey-BorweinPlouffe Pi Algorithm.
Elementos de Geometria Espacial
Introdução
A Geometria espacial (euclidiana)
funciona como uma ampliação da
Geometria plana (euclidiana) e trata
dos métodos apropriados para o
estudo de objetos espaciais assim
como a relação entre esses
elementos. Os objetos primitivos do
ponto de vista espacial, são: pontos,
retas, segmentos de retas, planos,
curvas, ângulos e superfícies. Os
principais tipos de cálculos que
podemos realizar são: comprimentos
de curvas, áreas de superfícies e
volumes
de
regiões
sólidas.
Tomaremos ponto, reta e plano
como conceitos primitivos, os quais
serão aceitos sem definição.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 89
Planos e retas
Um plano é um subconjunto do
espaço R3 de tal modo que
quaisquer
dois
pontos
desse
conjunto, podem ser ligados por um
segmento de reta inteiramente
contido no conjunto.
Duas retas (segmentos de reta) no
espaço R3 podem ser: paralelas,
concorrentes ou reversas.
Retas paralelas: Duas retas são
paralelas se elas não possuem
interseção e estão em um mesmo
plano.
Retas concorrentes: Duas retas são
concorrentes se elas têm um ponto
em comum. As retas perpendiculares
são retas concorrentes que formam
entre si um ângulo reto.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 90
Retas reversas: Duas retas são ditas
reversas quando uma não tem
interseção com a outra e elas não
são paralelas. Isto significa que elas
estão em planos diferentes. Pode-se
pensar de uma reta r desenhada no
chão de uma casa e uma reta s, não
paralela a r, desenhada no teto
dessa mesma casa.
Posições de pontos, retas e planos
Um plano no espaço R3 pode ser
determinado por qualquer uma das
situações:
1. Três pontos não colineares
(não pertencentes à mesma
reta).
2. Um ponto e uma reta ou um
segmento de reta que não
contém o ponto.
3. Um ponto e um segmento de
reta que não contém o ponto.
4. Duas retas paralelas que não
se sobrepõe.
5. Dois segmentos de reta
paralelos que não se sobrepõe.
6. Duas retas concorrentes.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 91
7. Dois segmentos
concorrentes.
de
reta
Posições de retas e planos
Há duas relações importantes,
relacionando uma reta e um plano no
espaço R3.
Reta paralela a um plano: Uma reta r
é paralela a um plano no espaço R3,
se existe uma reta s inteiramente
contida no plano que é paralela à
reta dada.
Reta perpendicular a um plano: Uma
reta é perpendicular a um plano no
espaço R3, se ela intersecta o plano
em um ponto P e todo segmento de
reta contido no plano que tem P
como uma de suas extremidades é
perpendicular à reta.
Distância de um ponto a um plano
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 92
Seja P um ponto localizado fora de
um plano. A distância do ponto ao
plano é a medida do segmento de
reta perpendicular ao plano em que
uma extremidade é o ponto P e a
outra extremidade é o ponto que é a
interseção entre o plano e o
segmento.
Se o ponto P estiver no plano, a
distância é nula.
Posições entre planos
1. Planos concorrentes no espaço
R3 são planos cuja interseção é
uma reta.
2. Planos paralelos no espaço R3
são planos que não tem
interseção.
3. Diedro: Quando dois planos
são concorrentes, dizemos que
tais planos formam um diedro.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 93
5. Planos normais são aqueles
cujo ângulo diedral é um
ângulo reto (90 graus).
4. Ângulo diedral: É ângulo
formado por dois planos
concorrentes. Para obter o
ângulo diedral, basta tomar o
ângulo formado por quaisquer
duas retas perpendiculares aos
planos concorrentes.
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 94
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 95
Autor: Carlos
Disciplina/matéria: Matematica/Supletivo
Assunto: Introdução – 1º período
Página : 96